2020春湘教版八下数学3.1平面直角坐标系教学课件(26张ppt)
文档属性
| 名称 | 2020春湘教版八下数学3.1平面直角坐标系教学课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 656.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览







文档简介
课件26张PPT。教学课件
数学 八年级下册 湘教版
第3章 图形与坐标
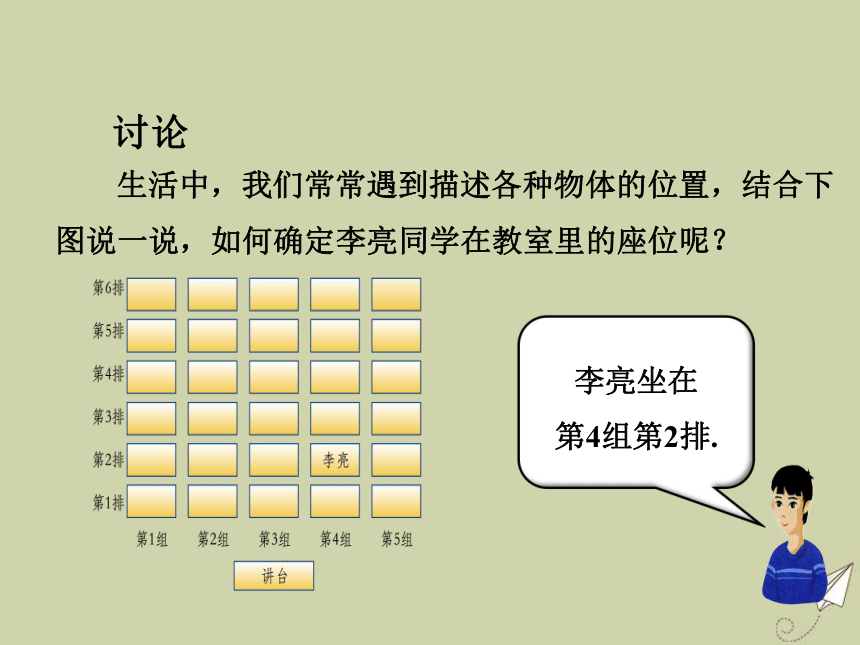
3.1 平面直角坐标系讨论 生活中,我们常常遇到描述各种物体的位置,结合下图说一说,如何确定李亮同学在教室里的座位呢?李亮坐在
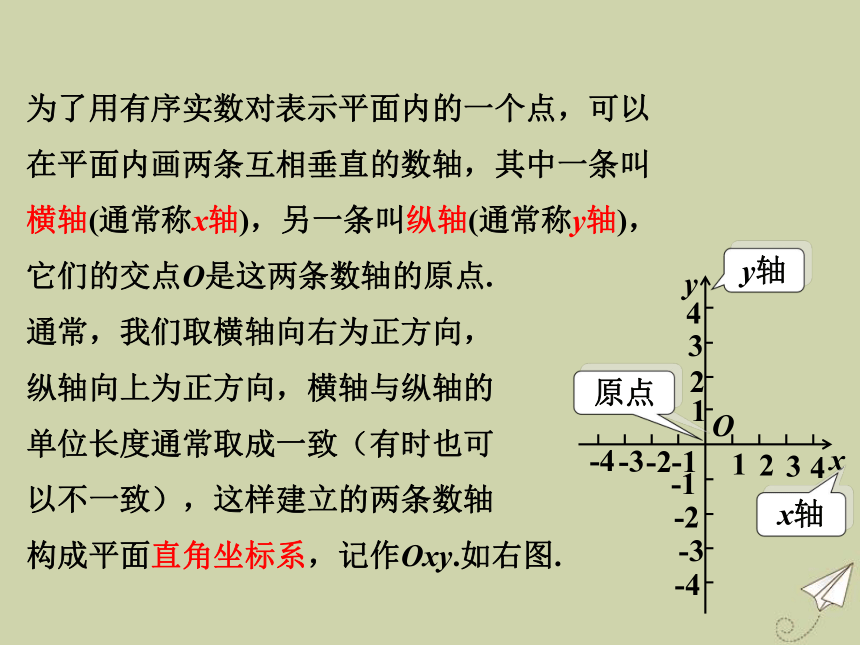
第4组第2排.从上面的例子可以看到,为了确定物体在平面上的位置,我们经常用“第4组第2排” 这样含有两个数的用语来确定物体的位置. 为了使这种方法更加简便,我们可以用一对有顺序的实数(简称为有序实数对)来表示.例如,李亮在教室里的座位可以简单地记作(4,2).怎样用有序实数对来表示平面内点的位置呢?从李亮在教室里的座位的例子可以看到,第4组是从横的方向来数的,第2排是从纵的方向来数的.为了用有序实数对表示平面内的一个点,可以在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称x轴),另一条叫纵轴(通常称y轴),它们的交点O是这两条数轴的原点.
通常,我们取横轴向右为正方向,
纵轴向上为正方向,横轴与纵轴的
单位长度通常取成一致(有时也可
以不一致),这样建立的两条数轴
构成平面直角坐标系,记作Oxy.如右图.如图,为了用有序实数表示点M,我们过点M作x轴的垂线,垂足为C,x轴上的点C表示-3;再过点M作y轴的垂线,垂足为D,y轴上的点D表示4,于是(-3,4)就表示了点M.我们把(-3,4)叫作
点M的坐标,其中-3叫作横坐标,
4叫作纵坐标.(-3,4)反之,为了指出坐标为(3,2)的点,我们在x轴上找到表示3的点A,过点A作x轴的垂线;再在y轴上找到表示2的点B,过点B作y轴的垂线,这两条垂线相交于点P,则点P就是坐标为(3,2)的点.P(3,2)综上所述,在建立了平面直角坐标系后,平面上的点与有序实数对一一对应.在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图的四个区域,我们把这四个区域分别称为第一,二,三,四象限,坐标轴上的点不属于任何一个象限.【例1】如图,写出平面直角坐标系中点A,B,C,D,E,F的坐标.解:所求各点的坐标为:
A(3,4),B(-4,3),
C(-3,0),D(-2,-4),E(0,-3),F(3,-3).【例2】在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限.
A(5,4),B(-3,4),
C (-4 ,-1),D(2,-4).点A在第一象限,点B在第二象限,点C在第三象限,点D在第四象限.结合例1、例2的解答,试说出平面直角坐标系中四个象限的点的坐标有什么特征,并填写下表:1. 如图,在平面直角坐标系中,
(1)写出点A,B,C,D,E的坐标;
(2)描出点P(-2,-1),Q(3,-2), S(2,5),T(-4,3) ,分别指出各点所在的象限.解:(1)A(3,3),B(-5 ,2),
C(-4,-3),D(4,-3),E(5,0).(2)描点略.点P在第三象限,点Q在第四象限,点S在第一象限,点T在第二象限.2. 在平面直角坐标系中,已知点P 在第四象限, 距离x轴2个单位长度,距离y轴3个单位长度, 则点P的坐标为 .答案:(3,-2).如图是某中学的校区平面示意图(一个方格的边长表示1个单位长度),试建立适当的平面直角坐标系,用坐标表示校门、图书馆、花坛、
体育场、教学大楼、国旗杆、
实验楼和体育馆的位置.如图,以校门所在的位置为原点,分别以正东、正北方向为x 轴、y轴的正方向,建立平面直角坐标系.6校门的位置为(0,0),图书馆的位置为(3,1), 花坛的位置为(3,4),体育场的位置为(4,7), 教学大楼的位置为(0,7),国旗杆的位置为(0,3), 实验楼的位置为(-4,6),体育馆的位置为(-3,2).【例3】根据以下条件画一幅示意图, 标出学校、书店、电影院、汽车站的位置.
(1)从学校向东走500m,再向北走450m到书店.
(2)从学校向西走300m,再向南走300m,最后向东走50m到电影院.
(3)从学校向南走600m,再向东走400m到汽车站.如图,以学校所在位置为原点,分别以正东、正北方向为x 轴, y 轴的正方向,建立平面直角坐标系, 规定1 个单位长度代表100 m长.根据题目条件,点A(5,4.5) 是书店的位置,点B(-2.5,-3)是电影院的位置, 点C(4,-6) 是汽车站的位置.在日常生活中, 除了用平面直角坐标系刻画物体之间的位置关系外,有时还可借助方向和距离(或称方位) 来刻画两物体的相对位置.(1)如图,李亮家距学校1000 m,如何用方向和距离来描述李亮家相对于学校的位置?(2)反过来,学校相对于李亮家的位置怎样描述呢?李亮家在学校的北偏西60°的方向上, 与学校的距离为1000 m; 反过来,学校在李亮家南偏东60°的方向上,与李亮家的距离为1000 m.我们把北偏西60°,南偏东60°这样的角称为方位角.【例4】如图,12 时我渔政船在H 岛正南方向,距H岛30海里的A 处,渔政船以每小时40 海里的速度向东航行, 13 时到达B处,并测得H 岛的方向是北偏西53°6′. 那么此时渔政船相对于H岛的位置怎样描述呢?分析:如图,设H 岛所在的位置为C,△ABC 是直角三角形, ∠CAB = 90°,利用勾股定理可以求出BC间的距离.3.如图是某动物园的部分平面示意图,试建立适当的平面直角坐标系, 用坐标表示大门、百鸟园、大象馆、狮子馆和猴山的位置.解:如图,以大门所在点为原点O,在网格中以过点O的水平直线和垂直直线分别作为x 轴,y 轴建立平面直角坐标系. 由图可知大门、百鸟园、大象馆、狮子馆和猴山的位置为:大门(0,0),百鸟园(5,3),大象馆(3,11),狮子馆(-2,7),猴山(-6,3).4.如图,通过测量(用刻度尺和量角器)回答下列问题:
(1)猴山在大门的北偏西_____°的方向上,到大门的距离大约为____m.
(2)百鸟园在狮子馆的南偏东__°的
方向上,到狮子馆的距离约为_____m.
(3)大象馆在大门的北偏东_____°
的方向上,到大门的距离约为_____m.5.如图,一艘海洋科考船在O点用雷达发现了几群鲸鱼,规定1个单位长度代表100m长,试用适当的方法来表示A, B, C, D, E这5个目标鱼群相对于点O的位置.解:A南偏东45°、300m处;B北偏东60°、300m处;
C北偏东45°、200m处;
D南偏西60°、200m处;
E北偏西30 ° 、500m处.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
数学 八年级下册 湘教版
第3章 图形与坐标
3.1 平面直角坐标系讨论 生活中,我们常常遇到描述各种物体的位置,结合下图说一说,如何确定李亮同学在教室里的座位呢?李亮坐在
第4组第2排.从上面的例子可以看到,为了确定物体在平面上的位置,我们经常用“第4组第2排” 这样含有两个数的用语来确定物体的位置. 为了使这种方法更加简便,我们可以用一对有顺序的实数(简称为有序实数对)来表示.例如,李亮在教室里的座位可以简单地记作(4,2).怎样用有序实数对来表示平面内点的位置呢?从李亮在教室里的座位的例子可以看到,第4组是从横的方向来数的,第2排是从纵的方向来数的.为了用有序实数对表示平面内的一个点,可以在平面内画两条互相垂直的数轴,其中一条叫横轴(通常称x轴),另一条叫纵轴(通常称y轴),它们的交点O是这两条数轴的原点.
通常,我们取横轴向右为正方向,
纵轴向上为正方向,横轴与纵轴的
单位长度通常取成一致(有时也可
以不一致),这样建立的两条数轴
构成平面直角坐标系,记作Oxy.如右图.如图,为了用有序实数表示点M,我们过点M作x轴的垂线,垂足为C,x轴上的点C表示-3;再过点M作y轴的垂线,垂足为D,y轴上的点D表示4,于是(-3,4)就表示了点M.我们把(-3,4)叫作
点M的坐标,其中-3叫作横坐标,
4叫作纵坐标.(-3,4)反之,为了指出坐标为(3,2)的点,我们在x轴上找到表示3的点A,过点A作x轴的垂线;再在y轴上找到表示2的点B,过点B作y轴的垂线,这两条垂线相交于点P,则点P就是坐标为(3,2)的点.P(3,2)综上所述,在建立了平面直角坐标系后,平面上的点与有序实数对一一对应.在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图的四个区域,我们把这四个区域分别称为第一,二,三,四象限,坐标轴上的点不属于任何一个象限.【例1】如图,写出平面直角坐标系中点A,B,C,D,E,F的坐标.解:所求各点的坐标为:
A(3,4),B(-4,3),
C(-3,0),D(-2,-4),E(0,-3),F(3,-3).【例2】在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限.
A(5,4),B(-3,4),
C (-4 ,-1),D(2,-4).点A在第一象限,点B在第二象限,点C在第三象限,点D在第四象限.结合例1、例2的解答,试说出平面直角坐标系中四个象限的点的坐标有什么特征,并填写下表:1. 如图,在平面直角坐标系中,
(1)写出点A,B,C,D,E的坐标;
(2)描出点P(-2,-1),Q(3,-2), S(2,5),T(-4,3) ,分别指出各点所在的象限.解:(1)A(3,3),B(-5 ,2),
C(-4,-3),D(4,-3),E(5,0).(2)描点略.点P在第三象限,点Q在第四象限,点S在第一象限,点T在第二象限.2. 在平面直角坐标系中,已知点P 在第四象限, 距离x轴2个单位长度,距离y轴3个单位长度, 则点P的坐标为 .答案:(3,-2).如图是某中学的校区平面示意图(一个方格的边长表示1个单位长度),试建立适当的平面直角坐标系,用坐标表示校门、图书馆、花坛、
体育场、教学大楼、国旗杆、
实验楼和体育馆的位置.如图,以校门所在的位置为原点,分别以正东、正北方向为x 轴、y轴的正方向,建立平面直角坐标系.6校门的位置为(0,0),图书馆的位置为(3,1), 花坛的位置为(3,4),体育场的位置为(4,7), 教学大楼的位置为(0,7),国旗杆的位置为(0,3), 实验楼的位置为(-4,6),体育馆的位置为(-3,2).【例3】根据以下条件画一幅示意图, 标出学校、书店、电影院、汽车站的位置.
(1)从学校向东走500m,再向北走450m到书店.
(2)从学校向西走300m,再向南走300m,最后向东走50m到电影院.
(3)从学校向南走600m,再向东走400m到汽车站.如图,以学校所在位置为原点,分别以正东、正北方向为x 轴, y 轴的正方向,建立平面直角坐标系, 规定1 个单位长度代表100 m长.根据题目条件,点A(5,4.5) 是书店的位置,点B(-2.5,-3)是电影院的位置, 点C(4,-6) 是汽车站的位置.在日常生活中, 除了用平面直角坐标系刻画物体之间的位置关系外,有时还可借助方向和距离(或称方位) 来刻画两物体的相对位置.(1)如图,李亮家距学校1000 m,如何用方向和距离来描述李亮家相对于学校的位置?(2)反过来,学校相对于李亮家的位置怎样描述呢?李亮家在学校的北偏西60°的方向上, 与学校的距离为1000 m; 反过来,学校在李亮家南偏东60°的方向上,与李亮家的距离为1000 m.我们把北偏西60°,南偏东60°这样的角称为方位角.【例4】如图,12 时我渔政船在H 岛正南方向,距H岛30海里的A 处,渔政船以每小时40 海里的速度向东航行, 13 时到达B处,并测得H 岛的方向是北偏西53°6′. 那么此时渔政船相对于H岛的位置怎样描述呢?分析:如图,设H 岛所在的位置为C,△ABC 是直角三角形, ∠CAB = 90°,利用勾股定理可以求出BC间的距离.3.如图是某动物园的部分平面示意图,试建立适当的平面直角坐标系, 用坐标表示大门、百鸟园、大象馆、狮子馆和猴山的位置.解:如图,以大门所在点为原点O,在网格中以过点O的水平直线和垂直直线分别作为x 轴,y 轴建立平面直角坐标系. 由图可知大门、百鸟园、大象馆、狮子馆和猴山的位置为:大门(0,0),百鸟园(5,3),大象馆(3,11),狮子馆(-2,7),猴山(-6,3).4.如图,通过测量(用刻度尺和量角器)回答下列问题:
(1)猴山在大门的北偏西_____°的方向上,到大门的距离大约为____m.
(2)百鸟园在狮子馆的南偏东__°的
方向上,到狮子馆的距离约为_____m.
(3)大象馆在大门的北偏东_____°
的方向上,到大门的距离约为_____m.5.如图,一艘海洋科考船在O点用雷达发现了几群鲸鱼,规定1个单位长度代表100m长,试用适当的方法来表示A, B, C, D, E这5个目标鱼群相对于点O的位置.解:A南偏东45°、300m处;B北偏东60°、300m处;
C北偏东45°、200m处;
D南偏西60°、200m处;
E北偏西30 ° 、500m处.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
