2020春湘教版八下数学3.3轴对称和平移的坐标表示教学课件(29张ppt)
文档属性
| 名称 | 2020春湘教版八下数学3.3轴对称和平移的坐标表示教学课件(29张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 362.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览







文档简介
课件29张PPT。教学课件
数学 八年级下册 湘教版
第3章 图形与坐标
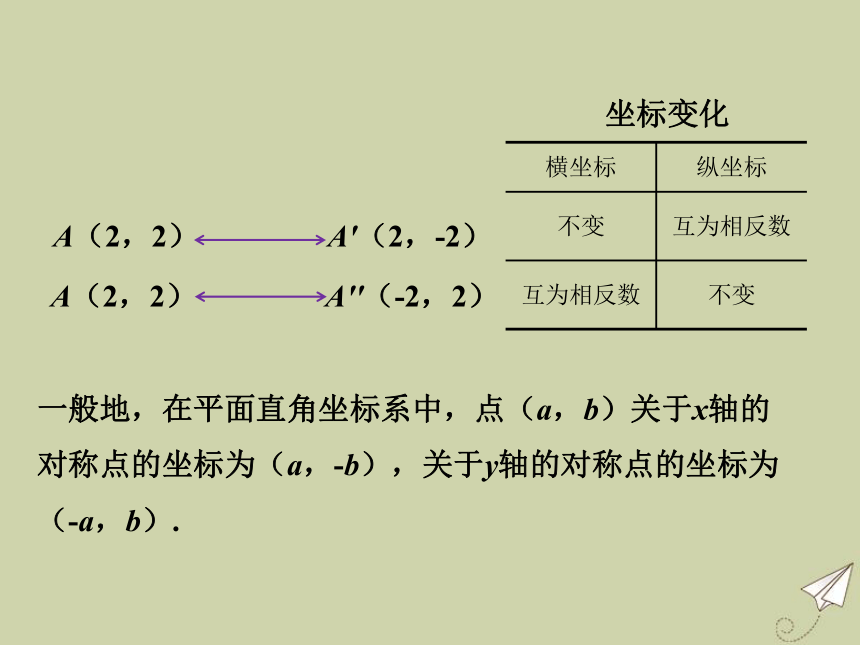
3.3 轴对称和平移的坐标表示如图,在平面直角坐标系中,点A的坐标为(2,2).
(1)分别作出点A关于x轴,y轴的对称点A',A'',并写出它们的坐标.
(2)比较:点A与A'的坐标之间有
什么关系?点A与A''呢?A'A''坐标变化一般地,在平面直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点的坐标为
(-a,b).作图如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
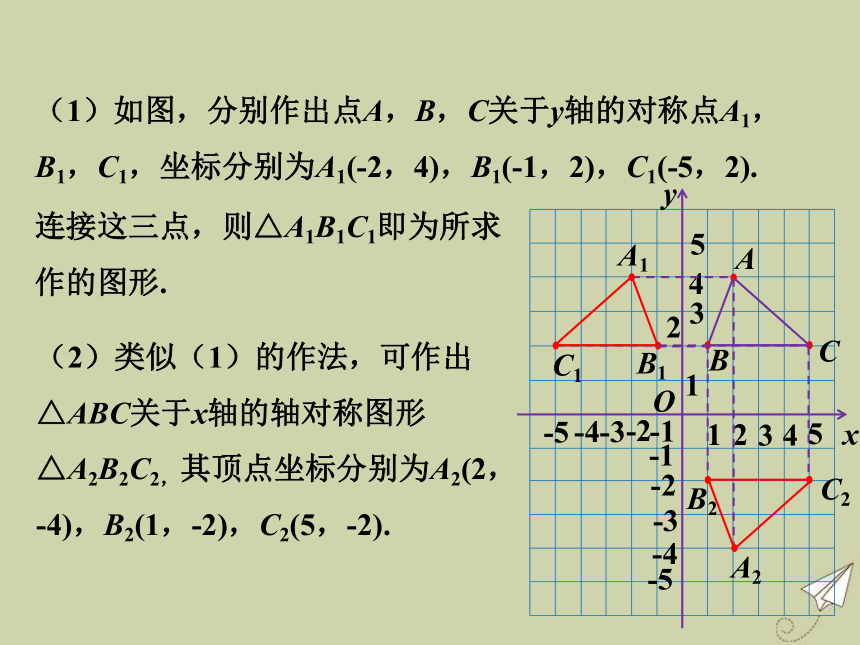
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.作一个图形关于坐标轴的轴对称图形,怎样画最简便呢?1、作出图形上各个顶点关于坐标轴的对称点.2、顺次连接对称点,所得的图形即为所求的对称图形.用上述方法解决该问题.(1)如图,分别作出点A,B,C关于y轴的对称点A1,B1,C1,坐标分别为A1(-2,4),B1(-1,2),C1(-5,2).连接这三点,则△A1B1C1即为所求作的图形.(2)类似(1)的作法,可作出△ABC关于x轴的轴对称图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2).【例1】 如图,求出折线OABCD各转折点的坐标以及它们关于y轴的对称点O′,A′,B′,C′,D′的坐标,并将点O′,A′,B′,C′,D′依次用线段连接起来.折线OABCD各转折点的坐标分别为O(0,0),A(2,1),B(3,3),C(3,5),D(0,5),它们关于y轴的对称点的坐标是O′(0,0),A′(-2,1),B′(-3,3),C′(-3,5),D′(0,5).将各点依次连接起来,得到如图.( O' )A' B' C' ( D' )1.填空.
(1)点B(2,-3)关于x轴对称的点的坐标是________;
(2)点A(-5,3)关于y轴对称的点的坐标是________.(2,3)(5,3)2.已知矩形ABCD的顶点坐标分别为A(-7,-2),
B(-7,-5),C(-3,-5),D(-3,-2),以y轴为对称轴作轴反射,矩形ABCD的像为矩形A′B′C′D′,求矩形A′B′C′D′的顶点坐标.解:矩形A′B′C′D′的顶点坐标分别是A′(7,-2),B′(7,-5),C′(3,-5),D′(3,-2).3.(1)如果点A(-4,a)与点A′(-4,-2)关于x轴对称,那么a的值为 .
(2)如果点B(-2,2b+1)与点B′(2,3)关于y轴对称,那么b的值为_______.21如图,在平面直角坐标系中,点A(1,2)
分别沿坐标轴方向作以下变换,试作点
A的像,并写出像的坐标.
(1)点A向右平移4个单位长度,像为点A1;
(2)点A向左平移3个单位长度,像为点A2;
(3)点A向上平移2个单位长度,像为点A3;
(4)点A向下平移4个单位长度,像为点A4.A1A2A3A4坐标变化一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位长度,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位长度,其像的坐标为(a,b+k)(或(a,b-k)).如图,线段AB的两个端点坐标分别为A(1,1),B(4,4),
(1)将线段AB向上平移2个单位,
作出它的像A′B′,并写出点A′,B′
的坐标.先作出A,B两点平移之后的点A',B',再连接A',B',则线段A'B'即为所求作的线段.
A'(3,1),B'(6,4).A'B'(2)若点C(x,y)是平面内任一点,在上述平移下,像点C′(x′,y′)与点C(x,y)的坐标有什么关系?C′(x′,y′)【例2】如图, △ABC的三个顶点坐标分别为A(3,3),
B(2,1),C(5,1) .
将△ABC向下平移5个单位,作出它的像,并写出像的顶点坐标.解:如图,将△ABC向下平移5个单位,则横坐标不变,纵坐标减5,由点A,B,C的坐标可知其像的坐标分别是A1(3,-2),B1(2,-4),C1(5,-4),依次连接点A1,B1,C1,即可得△ABC的像△A1B1C1.A1B1C11.填空:
(1)点A(-1,2)向右平移2个单位长度,它的像是A′ ;
(2)点B(2,-2)向下平移3个单位长度,它的像是B' .(1,2)(2,-5)2.如图,线段AB的两个端点坐标分别为A(-2,-2),B(2,2).将线段AB向下平移3个单位长度,它的像是线段A'B'.
(1)试写出点A',B'的坐标;
(2)若点C(x,y)是平面内的任一点,在上述平移下,像点C'(x',y')与点C(x,y)的坐标之间有什么关系?3.如图,正方形ABCD的顶点坐标分别为A(2,2),B(2,-2),C(6,-2),D(6,2),将正方形ABCD向左平移4个单位长度 ,作出它
的像,并写出像的顶点坐标.解:正方形ABCD向左平移4个单位的像为正方形A1B1C1D1,正方形各顶点的坐标为A ' (-2,2),B ' (-2,-2),C ' (2,
-2),D ' (2,2).新知探究如图,△ABC的顶点坐标分别为A(-4,-1),B(-5,-3),C(-2,-4).将△ABC向右平移7个单位长度,它的像是△A1B1C1;再向上平移5个单位长度,△A1B1C1的像是△A2B2C2.
(1)分别写出△A1B1C1,△A2B2C2的顶点坐标.
(2)将△ABC作沿射线AA2的方向的平移,移动的距离等于线段AA2的长度,则△ABC的像是△A2B2C2吗?(1)△A1B1C1的顶点坐标分别为:A1(3,-1),B1(2,-3),C1(5,-4);△A2B2C2的顶点坐标分别为:A2(3,4),B2(2,2),C2(5,1).(2)在这个平移下,点A(-4,-1)的像是点A2(3,4).点A2的横坐标是3=(-4)+7,点A2的纵坐标是4=(-1)+5.因此,在这个平移下,平面内任一点P(x,y)与其像点P'(x',y')的坐标有如下关系:按照 这个关系,点B(-5,-3)的像点的坐标为(2,2),从而点B的像的点是B2;点C(-2,-4)的像的点的坐标为(5,1),从而点C的像点是C2.因此△ABC的像是△A2B2C2.【例3】如图,四边形ABCD四个顶点的坐标分别为A(1,2),B(3,1),
C(5,2),D(3,4).将四边形
ABCD先向下平移5个单位长度,
再向左平移6个单位长度,它的像
是四边形A'B'C'D'.写出四边形
A'B'C'D'的顶点坐标,并作出该
四边形.如图,菱形ABCD四个顶点的坐标分别为A(4,7),B(2,4),C(4,1),D(6,4).将菱形ABCD向下平移3个单位长度,它的像是菱形A'B'C'D'.写出菱形A'B'C'D'的顶点坐标,并作出该图形.将菱形A'B'C'D'向左平移6个单位长度,它的像是菱形A''B''C''D'',写出菱形A''B''C''D''的顶点坐标,并作出该图形.解:菱形A'B'C'D'的顶点
坐标分别为A'(4,4),B'(2,1),C'(4,-2),D'(6,1),A''B''C''D''的顶点坐标分别为A''(-2,4),B''(-4,1),C''(-2,
-2),D''(0,1).
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
数学 八年级下册 湘教版
第3章 图形与坐标
3.3 轴对称和平移的坐标表示如图,在平面直角坐标系中,点A的坐标为(2,2).
(1)分别作出点A关于x轴,y轴的对称点A',A'',并写出它们的坐标.
(2)比较:点A与A'的坐标之间有
什么关系?点A与A''呢?A'A''坐标变化一般地,在平面直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点的坐标为
(-a,b).作图如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.作一个图形关于坐标轴的轴对称图形,怎样画最简便呢?1、作出图形上各个顶点关于坐标轴的对称点.2、顺次连接对称点,所得的图形即为所求的对称图形.用上述方法解决该问题.(1)如图,分别作出点A,B,C关于y轴的对称点A1,B1,C1,坐标分别为A1(-2,4),B1(-1,2),C1(-5,2).连接这三点,则△A1B1C1即为所求作的图形.(2)类似(1)的作法,可作出△ABC关于x轴的轴对称图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2).【例1】 如图,求出折线OABCD各转折点的坐标以及它们关于y轴的对称点O′,A′,B′,C′,D′的坐标,并将点O′,A′,B′,C′,D′依次用线段连接起来.折线OABCD各转折点的坐标分别为O(0,0),A(2,1),B(3,3),C(3,5),D(0,5),它们关于y轴的对称点的坐标是O′(0,0),A′(-2,1),B′(-3,3),C′(-3,5),D′(0,5).将各点依次连接起来,得到如图.( O' )A' B' C' ( D' )1.填空.
(1)点B(2,-3)关于x轴对称的点的坐标是________;
(2)点A(-5,3)关于y轴对称的点的坐标是________.(2,3)(5,3)2.已知矩形ABCD的顶点坐标分别为A(-7,-2),
B(-7,-5),C(-3,-5),D(-3,-2),以y轴为对称轴作轴反射,矩形ABCD的像为矩形A′B′C′D′,求矩形A′B′C′D′的顶点坐标.解:矩形A′B′C′D′的顶点坐标分别是A′(7,-2),B′(7,-5),C′(3,-5),D′(3,-2).3.(1)如果点A(-4,a)与点A′(-4,-2)关于x轴对称,那么a的值为 .
(2)如果点B(-2,2b+1)与点B′(2,3)关于y轴对称,那么b的值为_______.21如图,在平面直角坐标系中,点A(1,2)
分别沿坐标轴方向作以下变换,试作点
A的像,并写出像的坐标.
(1)点A向右平移4个单位长度,像为点A1;
(2)点A向左平移3个单位长度,像为点A2;
(3)点A向上平移2个单位长度,像为点A3;
(4)点A向下平移4个单位长度,像为点A4.A1A2A3A4坐标变化一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位长度,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位长度,其像的坐标为(a,b+k)(或(a,b-k)).如图,线段AB的两个端点坐标分别为A(1,1),B(4,4),
(1)将线段AB向上平移2个单位,
作出它的像A′B′,并写出点A′,B′
的坐标.先作出A,B两点平移之后的点A',B',再连接A',B',则线段A'B'即为所求作的线段.
A'(3,1),B'(6,4).A'B'(2)若点C(x,y)是平面内任一点,在上述平移下,像点C′(x′,y′)与点C(x,y)的坐标有什么关系?C′(x′,y′)【例2】如图, △ABC的三个顶点坐标分别为A(3,3),
B(2,1),C(5,1) .
将△ABC向下平移5个单位,作出它的像,并写出像的顶点坐标.解:如图,将△ABC向下平移5个单位,则横坐标不变,纵坐标减5,由点A,B,C的坐标可知其像的坐标分别是A1(3,-2),B1(2,-4),C1(5,-4),依次连接点A1,B1,C1,即可得△ABC的像△A1B1C1.A1B1C11.填空:
(1)点A(-1,2)向右平移2个单位长度,它的像是A′ ;
(2)点B(2,-2)向下平移3个单位长度,它的像是B' .(1,2)(2,-5)2.如图,线段AB的两个端点坐标分别为A(-2,-2),B(2,2).将线段AB向下平移3个单位长度,它的像是线段A'B'.
(1)试写出点A',B'的坐标;
(2)若点C(x,y)是平面内的任一点,在上述平移下,像点C'(x',y')与点C(x,y)的坐标之间有什么关系?3.如图,正方形ABCD的顶点坐标分别为A(2,2),B(2,-2),C(6,-2),D(6,2),将正方形ABCD向左平移4个单位长度 ,作出它
的像,并写出像的顶点坐标.解:正方形ABCD向左平移4个单位的像为正方形A1B1C1D1,正方形各顶点的坐标为A ' (-2,2),B ' (-2,-2),C ' (2,
-2),D ' (2,2).新知探究如图,△ABC的顶点坐标分别为A(-4,-1),B(-5,-3),C(-2,-4).将△ABC向右平移7个单位长度,它的像是△A1B1C1;再向上平移5个单位长度,△A1B1C1的像是△A2B2C2.
(1)分别写出△A1B1C1,△A2B2C2的顶点坐标.
(2)将△ABC作沿射线AA2的方向的平移,移动的距离等于线段AA2的长度,则△ABC的像是△A2B2C2吗?(1)△A1B1C1的顶点坐标分别为:A1(3,-1),B1(2,-3),C1(5,-4);△A2B2C2的顶点坐标分别为:A2(3,4),B2(2,2),C2(5,1).(2)在这个平移下,点A(-4,-1)的像是点A2(3,4).点A2的横坐标是3=(-4)+7,点A2的纵坐标是4=(-1)+5.因此,在这个平移下,平面内任一点P(x,y)与其像点P'(x',y')的坐标有如下关系:按照 这个关系,点B(-5,-3)的像点的坐标为(2,2),从而点B的像的点是B2;点C(-2,-4)的像的点的坐标为(5,1),从而点C的像点是C2.因此△ABC的像是△A2B2C2.【例3】如图,四边形ABCD四个顶点的坐标分别为A(1,2),B(3,1),
C(5,2),D(3,4).将四边形
ABCD先向下平移5个单位长度,
再向左平移6个单位长度,它的像
是四边形A'B'C'D'.写出四边形
A'B'C'D'的顶点坐标,并作出该
四边形.如图,菱形ABCD四个顶点的坐标分别为A(4,7),B(2,4),C(4,1),D(6,4).将菱形ABCD向下平移3个单位长度,它的像是菱形A'B'C'D'.写出菱形A'B'C'D'的顶点坐标,并作出该图形.将菱形A'B'C'D'向左平移6个单位长度,它的像是菱形A''B''C''D'',写出菱形A''B''C''D''的顶点坐标,并作出该图形.解:菱形A'B'C'D'的顶点
坐标分别为A'(4,4),B'(2,1),C'(4,-2),D'(6,1),A''B''C''D''的顶点坐标分别为A''(-2,4),B''(-4,1),C''(-2,
-2),D''(0,1).
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
