山东省潍坊市潍城区2019-2020学年八年级上学期期末考试数学试题(含答案)
文档属性
| 名称 | 山东省潍坊市潍城区2019-2020学年八年级上学期期末考试数学试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 494.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 21:16:33 | ||
图片预览



文档简介
2019—2020学年度第一学期期末质量检测
八年级数学试题2020.1
第I卷选择题(共36分)
一、选择题(本大题共12小题,在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分.)
1.下列电子元件符号不是轴对称图形的是( )
A. B. C. D.
2.要使分式有意义,则的取值范围是( )
A. B. C. D.
3.下列语句中,是命题的是( )
A.延长线段到 B.垂线段最短
C.画 D.等角的余角相等吗?
4.在平行四边形中,、的度数之比为,则的度数为( )
A. B. C. D.
5.小亮对一组数据16,18,20,20,3■,34进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,但小亮依然还能准确获得这组数据的( )
A.众数 B.方差 C.中位数 D.平均数
6.已知且,那么等于( )
A.0 B. C. D.没有意义
7.如图,在中,,点是边上的一点,点是的中点,若的垂直平分线经过点,,则( )
A.8 B.6 C.4 D.2
8.下列命题:①同旁内角互补,两直线平行;②若,则;③对角线互相垂直平分的四边形是正方形;④对顶角相等.其中逆命题是真命题的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形纸片中,,点是边上的一点,将纸片沿折叠,点落在处,恰好经过的中点,则的度数是( )
A. B. C. D.
10.某市为了处理污水需要铺设一条长为2000米的管道,实际施工时,×××××××,设原计划每天铺设管道米,则可列方程,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
A.每天比原计划多铺设10米,结果延期10天完成任务
B.每天比原计划少铺设10米,结果延期10天完成任务
C.每天比原计划少铺设10米,结果提前10天完成任务
D.每天比原计划多铺设10米,结果提前10天完成任务
11.如图,是的角平分线,是边上的一点,连接,使,且,则的度数是( )
A. B. C. D.
12.如图,在平行四边形中,平分,交于点,且,延长与的延长线交于点,连接,连接.下列结论中:①;②是等边角形:③;④;⑤.其中正确的是( )
A.②③⑤ B.①④⑤ C.①②③ D.①②④
第Ⅱ卷非选择题(共84分)
二、填空题(本大题共6小题共18分.只要求填写最后结果,每小题填对得3分.)
13.把命题“平行于同一条直线的两条直线平行”改写成“如果…,那么…”的形式:______.
14.某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下:
尺码/ 23.5 24 24.5 25 25.5 26 26.5
销量/双 3 7 6 16 18 8 2
由此你能给这家鞋店提供的进货建议是______.
15.如图,正方形,以为边向正方形内作等边,则______度.
16若关于的方程有解,则的取值范围是______.
17.如图,已知,,按如下步骤作图:
(1)分别以、为圆心,以大于的长为半径在两边作弧,交于两点、;
(2)经过、作直线,分别交、于点、;
(3)过点作交于点,连接、.
则下列结论:①、垂直平分;②;③平分;④四边形是菱形;⑤四边形是菱形.其中一定正确的是______(填序号).
18.如图,在四边形中,,,,,点是的中点.则______.
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.(1)化简:;
(2)化简分式:,并从中选一个你认为适合的整数代人求值.
20.(1)解方程:;
(2)解方程:.
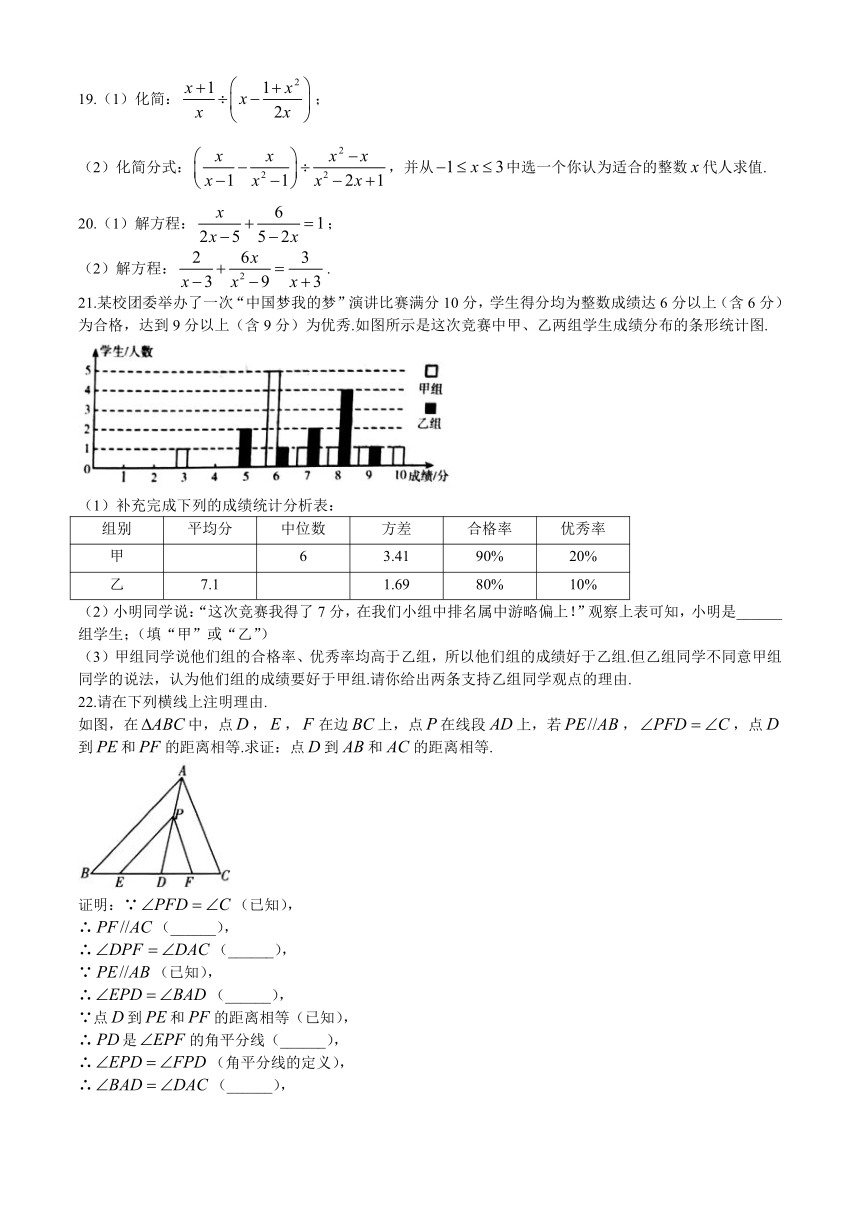
21.某校团委举办了一次“中国梦我的梦”演讲比赛满分10分,学生得分均为整数成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.如图所示是这次竞赛中甲、乙两组学生成绩分布的条形统计图.
(1)补充完成下列的成绩统计分析表:
组别 平均分 中位数 方差 合格率 优秀率
甲 6 3.41 90% 20%
乙 7.1 1.69 80% 10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是______组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
22.请在下列横线上注明理由.
如图,在中,点,,在边上,点在线段上,若,,点到和的距离相等.求证:点到和的距离相等.
证明:∵(已知),
∴(______),
∴(______),
∵(已知),
∴(______),
∵点到和的距离相等(已知),
∴是的角平分线(______),
∴(角平分线的定义),
∴(______),
即平分(角平分线的定义),
∴点到和的距离相等(______).
23.如图甲,正方形和正方形共一顶点,且点在上.连接并延长交于点.
(1)请猜想与的位置关系和数量关系,并说明理由;
(2)若点不在上,其它条件不变,如图乙.与是否还有上述关系?试说明理由.
24.潍坊市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨,下表是去年该酒店豪华间某两天的相关记录.
问:旺季每间价格为多少元?该酒店豪华间有多少间?
淡季 旺季
未入住间数 12 0
日总收入(元) 22800 40000
25.如图,平行四边形的对角线与相交于点,点为的中点,连接并延长交的延长线于点,连接.
(1)求证:;
(2)当,时,请判断四边形的形状,并证明你的结论.
(3)当四边形是正方形时,请判断的形状,并证明你的结论.
2019—2020学年度第一学期期末质量监测
八年级数学试题参考答案及评分标准
一.选择题(每小题3分,共36分)
1.C 2.D 3.B 4.A 5.C 6.B 7.C 8.B 9.A 10.D 11.C 12.D
二.填空题(每小题3分,共18分)
13. 如果两条直线平行于同一条直线,那么这两条直线平行 14. 多进25和25.5码的鞋 15.15 16.m≠1 17.①②④ 18.
三.解答题
19.(1)
(2)
要使原式有意义,则x≠1,-1,0
∴当x=2时,原式= 或当x=3时,原式=
(代入一个数计算即可)
20.(1)
解: x-6=2x-5
x=-1
检验:当x=-1时,2x -5≠0,所以x=-1是原方程的根.
(2)
解:2(x+3)+6x=3(x-3)
2x+6+6x=3x-9
5x=-15
x=-3
检验:当x=-3时,x2-9=0,所以x=-3是原方程的增根,原方程无解.
21.(1)甲组平均分6.7,乙组中位数7.5
(2)甲
(3)乙组的平均分高于甲组;乙组的中位数高于甲组,所以乙组的成绩要好于甲组.(答案不唯一)
22.证明:∠PFD=∠C(已知),
∴PF∥AC(同位角相等,两直线平行),
∴∠DPF=∠DAC(两直线平行,同位角相等).
PE∥AB(已知),
∴ ∠EPD=∠BAD(两直线平行,同位角相等).
点 D到PE和PF的距离相等(已知),
∴ PD是 ∠EPF的角平分线(角的内部到角的两边距离相等的点在角的平分线上),
∴ ∠EPD=∠FPD(角平分线的定义),
∴∠BAD=∠DAC (等量代换),
即AD平分∠BAC (角平分线的定义),
∴点D到AB和AC的距离相等(角平分线上的点到角的两边的距离相等)
23.(1)BG=DE,BG⊥DE.
理由:∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCG=∠DCE=90°,
∴△BCG≌△DCE(SAS),
∴BG=DE,
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
而∠BGC=∠DGH,
∴∠DHG=∠GCB=90°, 即BG⊥DE.
∴BG=DE,BG⊥DE;
(2)BG和DE还有上述关系:BG=DE,BG⊥DE.
∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCD=∠GCE=90°
∵∠BCG=∠BCD+∠DCG,∠DCE=∠GCE+∠DCG
∴∠BCG=∠DCE
∴△BCG≌△DCE,
∴BG=DE,∠CBG=∠CDE,
又∵∠BKC=∠DKH,
∴∠DHK=∠DCB=90° 即BG⊥DE.
∴BG=DE,BG⊥DE.
(
甲
乙
)
24.解:设淡季每间价格为x元,则旺季每间为x元.
根据题意得:
解得 x=600
经检验:x=600是原方程的解,且符合题意
∴x=800
豪华间数为50
答:旺季每间为800元,酒店豪华间有50间.
25.(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,
∴∠FDG=∠BAG,
∵点G 是AD的中点,
∴AG=DG
又∵∠FGD=∠BGA
∴△AGB≌△DGF(ASA)
∴AB=DF
∴DF=DC
(2)∵△AGB≌△DGF
∴GF=GB
又∵DG=AG
∴四边形ABDF是平行四边形
∵DG=DC,DC=DF,
∴DF=DG
在平行四边形ABCD中,∵∠ABC=120°,
∴∠ADC=120°
∴∠FDG=60°
∴△FDG为等边三角形
∴FG=DG
∴AD=BF
∴平行四边形ABDF是矩形.
(3)当四边形ABDF是正方形时,△FBC为等腰直角三角形.
证明:∵四边形ABDF是正方形
∴∠BFD=45°,∠FGD=90°
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠FBC =∠FGD = 90°
∴∠FCB = 45°=∠BFD
∴BF=BC,
∴△FBC为等腰直角三角形
(此题方法多样)
八年级数学试题2020.1
第I卷选择题(共36分)
一、选择题(本大题共12小题,在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分.)
1.下列电子元件符号不是轴对称图形的是( )
A. B. C. D.
2.要使分式有意义,则的取值范围是( )
A. B. C. D.
3.下列语句中,是命题的是( )
A.延长线段到 B.垂线段最短
C.画 D.等角的余角相等吗?
4.在平行四边形中,、的度数之比为,则的度数为( )
A. B. C. D.
5.小亮对一组数据16,18,20,20,3■,34进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,但小亮依然还能准确获得这组数据的( )
A.众数 B.方差 C.中位数 D.平均数
6.已知且,那么等于( )
A.0 B. C. D.没有意义
7.如图,在中,,点是边上的一点,点是的中点,若的垂直平分线经过点,,则( )
A.8 B.6 C.4 D.2
8.下列命题:①同旁内角互补,两直线平行;②若,则;③对角线互相垂直平分的四边形是正方形;④对顶角相等.其中逆命题是真命题的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形纸片中,,点是边上的一点,将纸片沿折叠,点落在处,恰好经过的中点,则的度数是( )
A. B. C. D.
10.某市为了处理污水需要铺设一条长为2000米的管道,实际施工时,×××××××,设原计划每天铺设管道米,则可列方程,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
A.每天比原计划多铺设10米,结果延期10天完成任务
B.每天比原计划少铺设10米,结果延期10天完成任务
C.每天比原计划少铺设10米,结果提前10天完成任务
D.每天比原计划多铺设10米,结果提前10天完成任务
11.如图,是的角平分线,是边上的一点,连接,使,且,则的度数是( )
A. B. C. D.
12.如图,在平行四边形中,平分,交于点,且,延长与的延长线交于点,连接,连接.下列结论中:①;②是等边角形:③;④;⑤.其中正确的是( )
A.②③⑤ B.①④⑤ C.①②③ D.①②④
第Ⅱ卷非选择题(共84分)
二、填空题(本大题共6小题共18分.只要求填写最后结果,每小题填对得3分.)
13.把命题“平行于同一条直线的两条直线平行”改写成“如果…,那么…”的形式:______.
14.某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下:
尺码/ 23.5 24 24.5 25 25.5 26 26.5
销量/双 3 7 6 16 18 8 2
由此你能给这家鞋店提供的进货建议是______.
15.如图,正方形,以为边向正方形内作等边,则______度.
16若关于的方程有解,则的取值范围是______.
17.如图,已知,,按如下步骤作图:
(1)分别以、为圆心,以大于的长为半径在两边作弧,交于两点、;
(2)经过、作直线,分别交、于点、;
(3)过点作交于点,连接、.
则下列结论:①、垂直平分;②;③平分;④四边形是菱形;⑤四边形是菱形.其中一定正确的是______(填序号).
18.如图,在四边形中,,,,,点是的中点.则______.
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.(1)化简:;
(2)化简分式:,并从中选一个你认为适合的整数代人求值.
20.(1)解方程:;
(2)解方程:.
21.某校团委举办了一次“中国梦我的梦”演讲比赛满分10分,学生得分均为整数成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.如图所示是这次竞赛中甲、乙两组学生成绩分布的条形统计图.
(1)补充完成下列的成绩统计分析表:
组别 平均分 中位数 方差 合格率 优秀率
甲 6 3.41 90% 20%
乙 7.1 1.69 80% 10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是______组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
22.请在下列横线上注明理由.
如图,在中,点,,在边上,点在线段上,若,,点到和的距离相等.求证:点到和的距离相等.
证明:∵(已知),
∴(______),
∴(______),
∵(已知),
∴(______),
∵点到和的距离相等(已知),
∴是的角平分线(______),
∴(角平分线的定义),
∴(______),
即平分(角平分线的定义),
∴点到和的距离相等(______).
23.如图甲,正方形和正方形共一顶点,且点在上.连接并延长交于点.
(1)请猜想与的位置关系和数量关系,并说明理由;
(2)若点不在上,其它条件不变,如图乙.与是否还有上述关系?试说明理由.
24.潍坊市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨,下表是去年该酒店豪华间某两天的相关记录.
问:旺季每间价格为多少元?该酒店豪华间有多少间?
淡季 旺季
未入住间数 12 0
日总收入(元) 22800 40000
25.如图,平行四边形的对角线与相交于点,点为的中点,连接并延长交的延长线于点,连接.
(1)求证:;
(2)当,时,请判断四边形的形状,并证明你的结论.
(3)当四边形是正方形时,请判断的形状,并证明你的结论.
2019—2020学年度第一学期期末质量监测
八年级数学试题参考答案及评分标准
一.选择题(每小题3分,共36分)
1.C 2.D 3.B 4.A 5.C 6.B 7.C 8.B 9.A 10.D 11.C 12.D
二.填空题(每小题3分,共18分)
13. 如果两条直线平行于同一条直线,那么这两条直线平行 14. 多进25和25.5码的鞋 15.15 16.m≠1 17.①②④ 18.
三.解答题
19.(1)
(2)
要使原式有意义,则x≠1,-1,0
∴当x=2时,原式= 或当x=3时,原式=
(代入一个数计算即可)
20.(1)
解: x-6=2x-5
x=-1
检验:当x=-1时,2x -5≠0,所以x=-1是原方程的根.
(2)
解:2(x+3)+6x=3(x-3)
2x+6+6x=3x-9
5x=-15
x=-3
检验:当x=-3时,x2-9=0,所以x=-3是原方程的增根,原方程无解.
21.(1)甲组平均分6.7,乙组中位数7.5
(2)甲
(3)乙组的平均分高于甲组;乙组的中位数高于甲组,所以乙组的成绩要好于甲组.(答案不唯一)
22.证明:∠PFD=∠C(已知),
∴PF∥AC(同位角相等,两直线平行),
∴∠DPF=∠DAC(两直线平行,同位角相等).
PE∥AB(已知),
∴ ∠EPD=∠BAD(两直线平行,同位角相等).
点 D到PE和PF的距离相等(已知),
∴ PD是 ∠EPF的角平分线(角的内部到角的两边距离相等的点在角的平分线上),
∴ ∠EPD=∠FPD(角平分线的定义),
∴∠BAD=∠DAC (等量代换),
即AD平分∠BAC (角平分线的定义),
∴点D到AB和AC的距离相等(角平分线上的点到角的两边的距离相等)
23.(1)BG=DE,BG⊥DE.
理由:∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCG=∠DCE=90°,
∴△BCG≌△DCE(SAS),
∴BG=DE,
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
而∠BGC=∠DGH,
∴∠DHG=∠GCB=90°, 即BG⊥DE.
∴BG=DE,BG⊥DE;
(2)BG和DE还有上述关系:BG=DE,BG⊥DE.
∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCD=∠GCE=90°
∵∠BCG=∠BCD+∠DCG,∠DCE=∠GCE+∠DCG
∴∠BCG=∠DCE
∴△BCG≌△DCE,
∴BG=DE,∠CBG=∠CDE,
又∵∠BKC=∠DKH,
∴∠DHK=∠DCB=90° 即BG⊥DE.
∴BG=DE,BG⊥DE.
(
甲
乙
)
24.解:设淡季每间价格为x元,则旺季每间为x元.
根据题意得:
解得 x=600
经检验:x=600是原方程的解,且符合题意
∴x=800
豪华间数为50
答:旺季每间为800元,酒店豪华间有50间.
25.(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,
∴∠FDG=∠BAG,
∵点G 是AD的中点,
∴AG=DG
又∵∠FGD=∠BGA
∴△AGB≌△DGF(ASA)
∴AB=DF
∴DF=DC
(2)∵△AGB≌△DGF
∴GF=GB
又∵DG=AG
∴四边形ABDF是平行四边形
∵DG=DC,DC=DF,
∴DF=DG
在平行四边形ABCD中,∵∠ABC=120°,
∴∠ADC=120°
∴∠FDG=60°
∴△FDG为等边三角形
∴FG=DG
∴AD=BF
∴平行四边形ABDF是矩形.
(3)当四边形ABDF是正方形时,△FBC为等腰直角三角形.
证明:∵四边形ABDF是正方形
∴∠BFD=45°,∠FGD=90°
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠FBC =∠FGD = 90°
∴∠FCB = 45°=∠BFD
∴BF=BC,
∴△FBC为等腰直角三角形
(此题方法多样)
同课章节目录
