2020春湘教版八下数学1.2直角三角形的性质和判定Ⅱ教学课件(35张)
文档属性
| 名称 | 2020春湘教版八下数学1.2直角三角形的性质和判定Ⅱ教学课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 863.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 17:24:42 | ||
图片预览



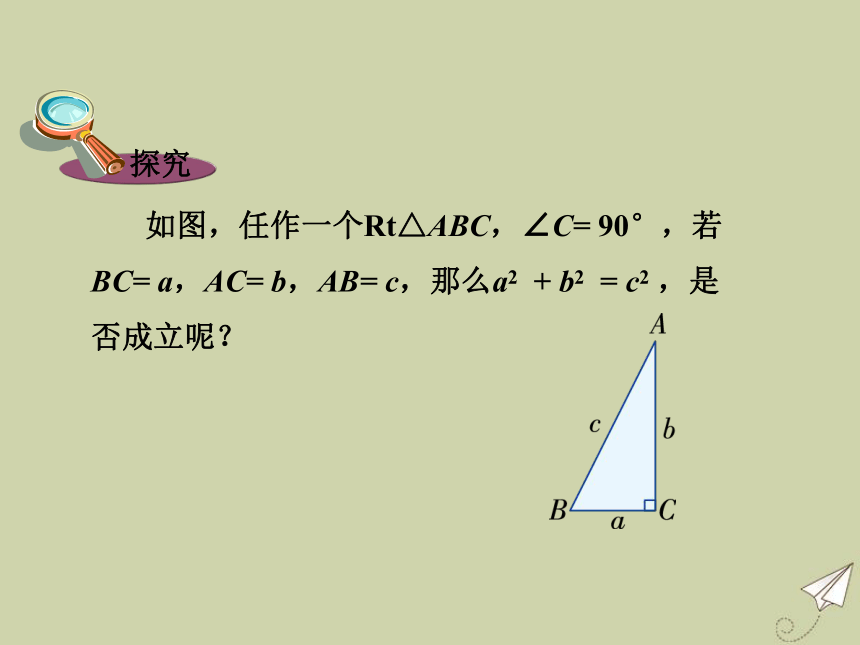






文档简介
课件35张PPT。教学课件
数学 八年级下册 湘教版
第1章 直角三角形
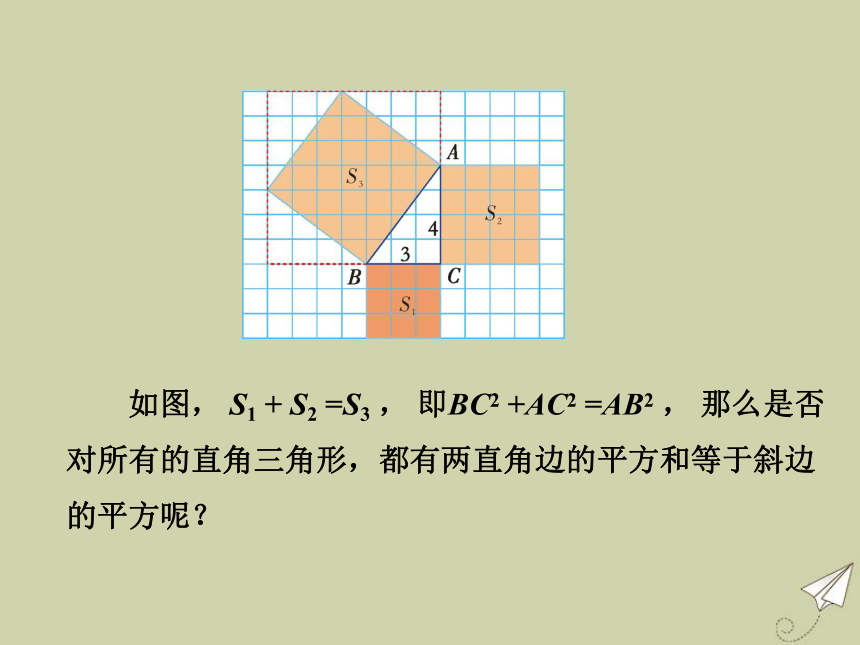
1.2 直角三角形的性质和判定(Ⅱ)直角三角形的性质 和判定( Ⅱ )1.2 如图, S1 + S2 =S3 , 即BC2 +AC2 =AB2 , 那么是否对所有的直角三角形,都有两直角边的平方和等于斜边的平方呢? 如图,任作一个Rt△ABC,∠C= 90°,若BC= a,AC= b,AB= c,那么a2 + b2 = c2 ,是
否成立呢?步骤1 先剪出4个如图1-11 的直角三角形, 由
于每个直角三角形的两直角边长为a,b(其中
b > a),因此它们全等(SAS),所以它们的
斜边长相等. 设斜边长为c.
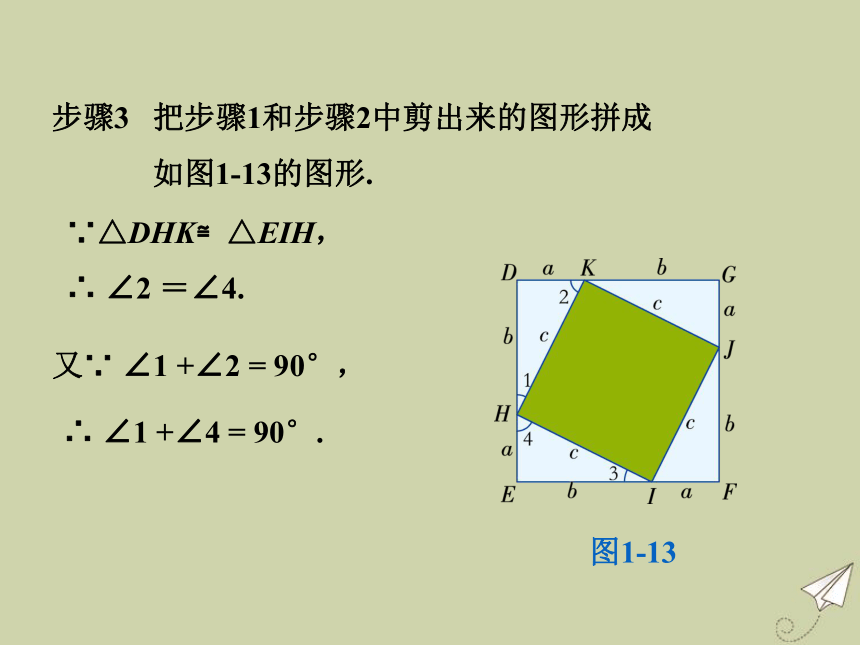
我们来进行研究.步骤2 再剪出1 个边长为c 的正方形,如图1-12.图1-12步骤3 把步骤1和步骤2中剪出来的图形拼成
如图1-13的图形.∵△DHK≌△EIH,
∴ ∠2 =∠4.又∵ ∠1 +∠2 = 90°,∴ ∠1 +∠4 = 90°.因此拼成的图形是正方形DEFG,
它的边长为(a + b),它的面积为
(a + b)2 .又∵∠KHI = 90°,
∴ ∠1 +∠KHI +∠4 = 180°,
即点D,H,E 在一条直线上.同理,点E,I,F在一条直线上;点 F ,J,G 在一条直
线上; 点G ,K,D 在一条直线上.直角三角形的两直角边a,b的平方和,等于斜边c的平方. a2+ b2 = c2 由此得到直角三角形的性质定理: 其实我国早在三千多年前就已经知道直角三
角形的上述性质,由于古人称直角三角形的直角
边中较短的一边为勾,较长的一边为股,斜边为
弦(如图1-14),因此这一性质被称为勾股定理. 勾股定理揭示了直角三角形三边之间的关系. 在直角三角形中,若已知直角三角形任意两条边长, 我们可以根据勾股定理,求出第三边的长.勾股弦图1-14故AD的长为12 cm.在Rt△ADB中,由勾股定理,得
AD2+BD2 =AB2 ,在Rt△ABC中,∠C= 90°.
(1) 已知a = 25,b = 15,求c;
(2) 已知a = 5,c = 9,求b;
(3) 已知b = 5,c=15,求a. 如图1-16,电工师傅把4 m长的梯子AC 靠在
墙上,使梯脚C 离墙脚B 的距离为1.5 m,准备在
墙上安装电灯. 当他爬上梯子后,发现高度不够,
于是将梯脚往墙脚移近0.5 m,即移
动到C′处. 那么梯子顶端是否往上
移动0.5 m 呢?图1-16在Rt△ABC中,AC=4 m,BC=1.5 m,
即梯子顶端A点大约向上移动了0.16 m,而不是向上
移动0.5 m.
在Rt△ACB′中, 根据勾股定理,得
x2 + 52 =(x+ 1)2,答:水池的深度为12尺,芦苇长为13尺.图1-18因为正方形池塘的边长为10尺, 所以
B′C = 5尺.解得 x=12.
则x + 1 =13.1. 如图,一艘渔船以30 海里/时 的速度由西向东追赶 鱼群. 在A 处测得小岛C 在船的北偏东60°方向;40 min 后,渔船行至B 处,此时测得小岛C 在船的北偏东30°方向. 已知以小岛C 为中心,周围10 海里以内有暗礁,问:这艘渔船继续向东追赶鱼群是否有触礁的危险?解:过点C作CD⊥AB,垂足为D,DCD的距离不在以点C为中心,周围10 海里范围内,
∴轮船不会触礁.在Rt△CBD中,∠BCD=30°,
BC=AB=20海里,∴ BD=10海里.
2. 如图,AE 是位于公路边的电线杆,高为12 m,
为了使电线CDE 不影响汽车的正常行驶,电力
部门在公路的另一边竖立了一根高为6 m的水泥
撑杆BD,用于撑起电线.已知两根杆子之间的距
离为8 m,电线CD 与水平线AC 的夹角为60°.
求电线CDE 的总长L(A,B,C 三点
在同一直线上,电线杆、水泥杆的粗
细忽略不计).M易知四边形MABD为矩形,所以MA=BD=6 m,所以ME=EA-MA=12-6=6(m). 我们已经知道勾股定理:“直角三角形两直角边a,b 的平方和,等于斜边c的平方.” 那么这个定理的逆命题成立吗? 如图1-19,在△ABC 中,AB = c,BC = a,AC = b,
且a2+ b2 =c2 , 那么△ABC是直角三角形吗?图1-19∵ a2+ b2 = c2 ,图1-20∴ △ABC是直角三角形. 先构造满足某些条件的
图形,再根据所求证的图
形与所构造图形之间的关系,
完成证明,这也是常用的问
题解决策略.如果三角形的三条边长a,b,c 满足关系: ,那么这个三角形是直角三角形. 由此得到直角三角形的判定定理:上述定理被称为勾股定理的逆定理.分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.例4如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.图1-21答:(1)是 ; (2)不是; (3)是.例 如图,在Rt△ABD中,∠D=90°,C为AD上一点, 则x可能是( ).
A.10° B.20° C.30° D.40°B
数学 八年级下册 湘教版
第1章 直角三角形
1.2 直角三角形的性质和判定(Ⅱ)直角三角形的性质 和判定( Ⅱ )1.2 如图, S1 + S2 =S3 , 即BC2 +AC2 =AB2 , 那么是否对所有的直角三角形,都有两直角边的平方和等于斜边的平方呢? 如图,任作一个Rt△ABC,∠C= 90°,若BC= a,AC= b,AB= c,那么a2 + b2 = c2 ,是
否成立呢?步骤1 先剪出4个如图1-11 的直角三角形, 由
于每个直角三角形的两直角边长为a,b(其中
b > a),因此它们全等(SAS),所以它们的
斜边长相等. 设斜边长为c.
我们来进行研究.步骤2 再剪出1 个边长为c 的正方形,如图1-12.图1-12步骤3 把步骤1和步骤2中剪出来的图形拼成
如图1-13的图形.∵△DHK≌△EIH,
∴ ∠2 =∠4.又∵ ∠1 +∠2 = 90°,∴ ∠1 +∠4 = 90°.因此拼成的图形是正方形DEFG,
它的边长为(a + b),它的面积为
(a + b)2 .又∵∠KHI = 90°,
∴ ∠1 +∠KHI +∠4 = 180°,
即点D,H,E 在一条直线上.同理,点E,I,F在一条直线上;点 F ,J,G 在一条直
线上; 点G ,K,D 在一条直线上.直角三角形的两直角边a,b的平方和,等于斜边c的平方. a2+ b2 = c2 由此得到直角三角形的性质定理: 其实我国早在三千多年前就已经知道直角三
角形的上述性质,由于古人称直角三角形的直角
边中较短的一边为勾,较长的一边为股,斜边为
弦(如图1-14),因此这一性质被称为勾股定理. 勾股定理揭示了直角三角形三边之间的关系. 在直角三角形中,若已知直角三角形任意两条边长, 我们可以根据勾股定理,求出第三边的长.勾股弦图1-14故AD的长为12 cm.在Rt△ADB中,由勾股定理,得
AD2+BD2 =AB2 ,在Rt△ABC中,∠C= 90°.
(1) 已知a = 25,b = 15,求c;
(2) 已知a = 5,c = 9,求b;
(3) 已知b = 5,c=15,求a. 如图1-16,电工师傅把4 m长的梯子AC 靠在
墙上,使梯脚C 离墙脚B 的距离为1.5 m,准备在
墙上安装电灯. 当他爬上梯子后,发现高度不够,
于是将梯脚往墙脚移近0.5 m,即移
动到C′处. 那么梯子顶端是否往上
移动0.5 m 呢?图1-16在Rt△ABC中,AC=4 m,BC=1.5 m,
即梯子顶端A点大约向上移动了0.16 m,而不是向上
移动0.5 m.
在Rt△ACB′中, 根据勾股定理,得
x2 + 52 =(x+ 1)2,答:水池的深度为12尺,芦苇长为13尺.图1-18因为正方形池塘的边长为10尺, 所以
B′C = 5尺.解得 x=12.
则x + 1 =13.1. 如图,一艘渔船以30 海里/时 的速度由西向东追赶 鱼群. 在A 处测得小岛C 在船的北偏东60°方向;40 min 后,渔船行至B 处,此时测得小岛C 在船的北偏东30°方向. 已知以小岛C 为中心,周围10 海里以内有暗礁,问:这艘渔船继续向东追赶鱼群是否有触礁的危险?解:过点C作CD⊥AB,垂足为D,DCD的距离不在以点C为中心,周围10 海里范围内,
∴轮船不会触礁.在Rt△CBD中,∠BCD=30°,
BC=AB=20海里,∴ BD=10海里.
2. 如图,AE 是位于公路边的电线杆,高为12 m,
为了使电线CDE 不影响汽车的正常行驶,电力
部门在公路的另一边竖立了一根高为6 m的水泥
撑杆BD,用于撑起电线.已知两根杆子之间的距
离为8 m,电线CD 与水平线AC 的夹角为60°.
求电线CDE 的总长L(A,B,C 三点
在同一直线上,电线杆、水泥杆的粗
细忽略不计).M易知四边形MABD为矩形,所以MA=BD=6 m,所以ME=EA-MA=12-6=6(m). 我们已经知道勾股定理:“直角三角形两直角边a,b 的平方和,等于斜边c的平方.” 那么这个定理的逆命题成立吗? 如图1-19,在△ABC 中,AB = c,BC = a,AC = b,
且a2+ b2 =c2 , 那么△ABC是直角三角形吗?图1-19∵ a2+ b2 = c2 ,图1-20∴ △ABC是直角三角形. 先构造满足某些条件的
图形,再根据所求证的图
形与所构造图形之间的关系,
完成证明,这也是常用的问
题解决策略.如果三角形的三条边长a,b,c 满足关系: ,那么这个三角形是直角三角形. 由此得到直角三角形的判定定理:上述定理被称为勾股定理的逆定理.分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.例4如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.图1-21答:(1)是 ; (2)不是; (3)是.例 如图,在Rt△ABD中,∠D=90°,C为AD上一点, 则x可能是( ).
A.10° B.20° C.30° D.40°B
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
