人教版2019-2020学年下学期九年级数学专题复习资料二:利用相似三角形的基本图形破题(无答案)
文档属性
| 名称 | 人教版2019-2020学年下学期九年级数学专题复习资料二:利用相似三角形的基本图形破题(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 339.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览

文档简介
九年级数学下学期专题复习资料 二
利用相似三角形的基本图形破题
注:本复习相似三角形的判定和基本性质为主. 编制:赵化中学 郑宗平
一.知识链接
1相似三角形的性质:
⑴. 相似三角形的对应角相等。对应边成比例;
⑵.相似三角形对应的中线之比、角平分之比、高线之比等于相似比;
⑶.相似三角形的周长之比等于相似比;
⑷.相似三角形的面积比等于相似比的平方. ……
2.三角形相似的判定:
⑴.三角对应相等、三边对应成比例的两个三角形相似;(定义法)
⑵.平行于三角形一边截其它两边或两边的延长线所构成的三角形与原三角形相似;(平行定理)
⑶.三边对应成比例的两个三角形相似;(两角定理)
⑷.有两边对应成比例,且它们的夹角对应相等的两个三角形相似;(两边夹角定理)
⑸.两角对应相等的两个三角形相似;(两角定理)
⑹.有斜边和直角边对应成比例的两个直角三角形相似.(斜边直角边定理)
二.基本图形研究
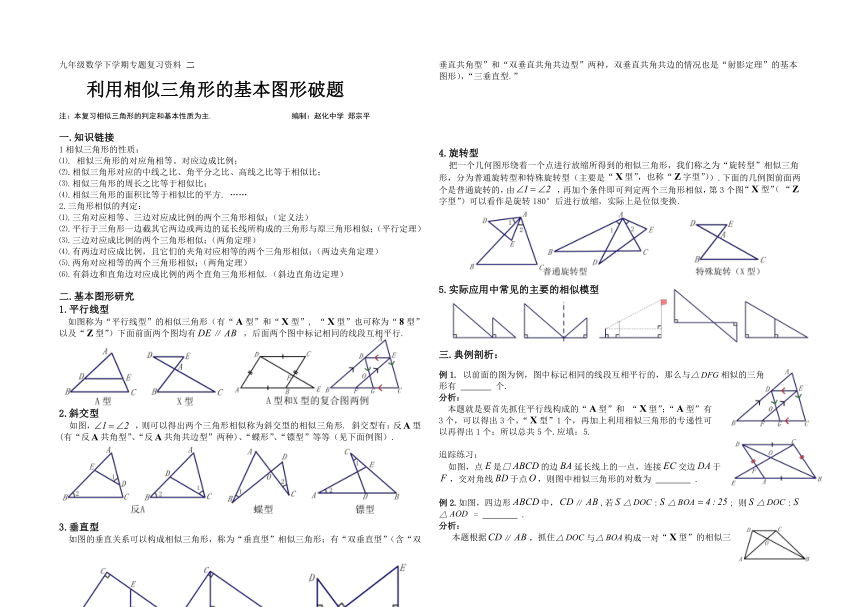
1.平行线型
如图称为“平行线型”的相似三角形(有“型”和“型”, “型”也可称为“型”以及“型”)下面前面两个图均有∥ ,后面两个图中标记相同的线段互相平行.
2.斜交型
如图, ,则可以得出两个三角形相似称为斜交型的相似三角形. 斜交型有:反型 (有“反共角型”、“反共角共边型”两种)、“蝶形”、“镖型”等等(见下面例图).
3.垂直型
如图的垂直关系可以构成相似三角形,称为“垂直型”相似三角形;有“双垂直型”(含“双垂直共角型”和“双垂直共角共边型”两种,双垂直共角共边的情况也是“射影定理”的基本图形),“三垂直型.”
4.旋转型
把一个几何图形绕着一个点进行放缩所得到的相似三角形,我们称之为“旋转型”相似三角形,分为普通旋转型和特殊旋转型(主要是“型”,也称“字型”)).下面的几例图前面两个是普通旋转的,由 ,再加个条件即可判定两个三角形相似,第3个图“型”( “字型”)可以看作是旋转180°后进行放缩,实际上是位似变换.
5.实际应用中常见的主要的相似模型
三.典例剖析:
例1. 以前面的图为例,图中标记相同的线段互相平行的,那么与△相似的三角
形有 个.
分析:
本题就是要首先抓住平行线构成的“型”和 “型”;“型”有
3个,可以得出3个,“型”1个,再加上利用相似三角形的专递性可
以再得出1个;所以总共5个.应填:5.
追踪练习:
如图,点是□的边延长线上的一点,连接交边于
,交对角线于点,则图中相似三角形的对数为 .
例2.如图,四边形中,∥,若△:△; 则△:△ = .
分析:
本题根据∥,抓住△与△构成一对“型”的相似三
角形,利用“相似三角形的面积比是相似比的的平方”可求;
而△和△底边同在一直线上, 其高相同,故△:△
=;故应填:.
追踪练习:
1..如图,已知在梯形中,∥,,如果对角线
与相交于点,△、△、△、△的面积分别记
作,那么下面结论中,不正确的是 ( )
A. B. C. D.
2.如图,是△的边上的两点。且,过
作∥,∥交分别为;若设△、四边形
、四边形的面积分别为,则( )
A. B. C. D.
例3. 如图从⊙外一点向圆引两条割线,交点情况见图.
⑴.求证:
⑵.若,求的长?
分析:
本题主要是⑴问,把等积式化成比列式;
不难发现连接构成一个“反共角型”,三点定形法把问题
转化为△∽△来解决; 本题的⑵问把数据代入⑴问即可求
得的长.
追踪练习:
1.如图,已知,;求的长.
2.如图,已知为⊙外的一点,过点引⊙的切线,切点
为,引割线;若;求的长.
例4. 如图,点三点在同一直线线, ,垂足分别为点; 若,求的长.
分析:
本题利用垂直和互余关系可以得到,进而证明
△∽△ (是“三垂直型”的相似三角形),∴,利
用勾股定理可求得 , 结合已知有,解得:.
追踪练习:
如图,为⊙的直径,垂直于弦(不是直径),垂足为.
⑴. 求证:;
⑵.若,求的长?
四.巩固练习
1.如图,点为△边上的一点,若过点画一直线
与△两边相交所截得的三角形与△相似,这样的直
线可以画多少条?请在右上图中画出草图.
3. 如图,△与△有.求证:
4.如图,已知.求证:△∽△
5.如图,为菱形的边的反向延长线的一点,连结交于点;连结,过点作∥交于.求证:
6.如图,在△中,,为上的一点,且点不与点重合,过点作交边于点,点不与点重合;若,设的长为,四边形的周长为.
⑴.求证:△∽△;
⑵.写出与的函数关系式,并在直角坐标系中画出函数图象.
7.如图,△是一块锐角三角形的余料,边,高,要把它加工成正方形零件,使正方形一边在上,其余两个顶点分别在上,那么这个正方形零件的边长应是多少?
变式:其余条件不变,把“正方形零件”改为“宽与长之
比为的矩形零件”,求此矩形的长与宽分别是多少?
2020.3.27编制
利用相似三角形的基本图形破题
注:本复习相似三角形的判定和基本性质为主. 编制:赵化中学 郑宗平
一.知识链接
1相似三角形的性质:
⑴. 相似三角形的对应角相等。对应边成比例;
⑵.相似三角形对应的中线之比、角平分之比、高线之比等于相似比;
⑶.相似三角形的周长之比等于相似比;
⑷.相似三角形的面积比等于相似比的平方. ……
2.三角形相似的判定:
⑴.三角对应相等、三边对应成比例的两个三角形相似;(定义法)
⑵.平行于三角形一边截其它两边或两边的延长线所构成的三角形与原三角形相似;(平行定理)
⑶.三边对应成比例的两个三角形相似;(两角定理)
⑷.有两边对应成比例,且它们的夹角对应相等的两个三角形相似;(两边夹角定理)
⑸.两角对应相等的两个三角形相似;(两角定理)
⑹.有斜边和直角边对应成比例的两个直角三角形相似.(斜边直角边定理)
二.基本图形研究
1.平行线型
如图称为“平行线型”的相似三角形(有“型”和“型”, “型”也可称为“型”以及“型”)下面前面两个图均有∥ ,后面两个图中标记相同的线段互相平行.
2.斜交型
如图, ,则可以得出两个三角形相似称为斜交型的相似三角形. 斜交型有:反型 (有“反共角型”、“反共角共边型”两种)、“蝶形”、“镖型”等等(见下面例图).
3.垂直型
如图的垂直关系可以构成相似三角形,称为“垂直型”相似三角形;有“双垂直型”(含“双垂直共角型”和“双垂直共角共边型”两种,双垂直共角共边的情况也是“射影定理”的基本图形),“三垂直型.”
4.旋转型
把一个几何图形绕着一个点进行放缩所得到的相似三角形,我们称之为“旋转型”相似三角形,分为普通旋转型和特殊旋转型(主要是“型”,也称“字型”)).下面的几例图前面两个是普通旋转的,由 ,再加个条件即可判定两个三角形相似,第3个图“型”( “字型”)可以看作是旋转180°后进行放缩,实际上是位似变换.
5.实际应用中常见的主要的相似模型
三.典例剖析:
例1. 以前面的图为例,图中标记相同的线段互相平行的,那么与△相似的三角
形有 个.
分析:
本题就是要首先抓住平行线构成的“型”和 “型”;“型”有
3个,可以得出3个,“型”1个,再加上利用相似三角形的专递性可
以再得出1个;所以总共5个.应填:5.
追踪练习:
如图,点是□的边延长线上的一点,连接交边于
,交对角线于点,则图中相似三角形的对数为 .
例2.如图,四边形中,∥,若△:△; 则△:△ = .
分析:
本题根据∥,抓住△与△构成一对“型”的相似三
角形,利用“相似三角形的面积比是相似比的的平方”可求;
而△和△底边同在一直线上, 其高相同,故△:△
=;故应填:.
追踪练习:
1..如图,已知在梯形中,∥,,如果对角线
与相交于点,△、△、△、△的面积分别记
作,那么下面结论中,不正确的是 ( )
A. B. C. D.
2.如图,是△的边上的两点。且,过
作∥,∥交分别为;若设△、四边形
、四边形的面积分别为,则( )
A. B. C. D.
例3. 如图从⊙外一点向圆引两条割线,交点情况见图.
⑴.求证:
⑵.若,求的长?
分析:
本题主要是⑴问,把等积式化成比列式;
不难发现连接构成一个“反共角型”,三点定形法把问题
转化为△∽△来解决; 本题的⑵问把数据代入⑴问即可求
得的长.
追踪练习:
1.如图,已知,;求的长.
2.如图,已知为⊙外的一点,过点引⊙的切线,切点
为,引割线;若;求的长.
例4. 如图,点三点在同一直线线, ,垂足分别为点; 若,求的长.
分析:
本题利用垂直和互余关系可以得到,进而证明
△∽△ (是“三垂直型”的相似三角形),∴,利
用勾股定理可求得 , 结合已知有,解得:.
追踪练习:
如图,为⊙的直径,垂直于弦(不是直径),垂足为.
⑴. 求证:;
⑵.若,求的长?
四.巩固练习
1.如图,点为△边上的一点,若过点画一直线
与△两边相交所截得的三角形与△相似,这样的直
线可以画多少条?请在右上图中画出草图.
3. 如图,△与△有.求证:
4.如图,已知.求证:△∽△
5.如图,为菱形的边的反向延长线的一点,连结交于点;连结,过点作∥交于.求证:
6.如图,在△中,,为上的一点,且点不与点重合,过点作交边于点,点不与点重合;若,设的长为,四边形的周长为.
⑴.求证:△∽△;
⑵.写出与的函数关系式,并在直角坐标系中画出函数图象.
7.如图,△是一块锐角三角形的余料,边,高,要把它加工成正方形零件,使正方形一边在上,其余两个顶点分别在上,那么这个正方形零件的边长应是多少?
变式:其余条件不变,把“正方形零件”改为“宽与长之
比为的矩形零件”,求此矩形的长与宽分别是多少?
2020.3.27编制
