人教版2019-2020学年下学期九年级数学第29章投影与视图专题复习资料(常见考点例举、无答案)
文档属性
| 名称 | 人教版2019-2020学年下学期九年级数学第29章投影与视图专题复习资料(常见考点例举、无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览


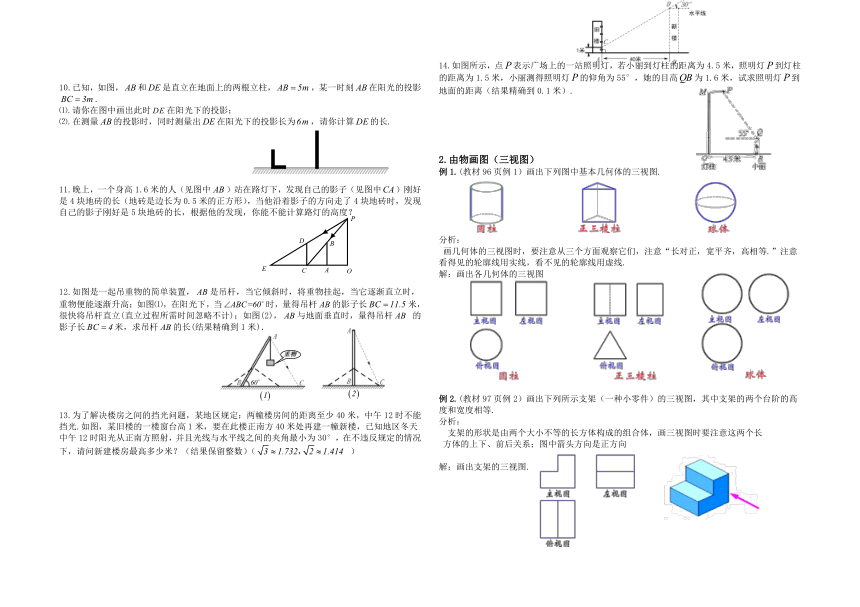
文档简介
九年级数学下学期专题复习资料 五
《投影与视图》常见考点例举
注:本复习以《投影与视图》的内容为主.
一.知识链接
1.投影的定义、投影线、投影面;
2.投影的分类:
⑴.平行投影(投影线互相平行,即平行光线):①.斜投影(投影线与投影面斜交);②.正投影(投影光线与投影面垂直);
⑵.中心投影(投影线集中一点,即点光源形成的).
3.正投影的性质:
注:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
4.平行投影与中心投影
的区别与联系
5.视图的定义关键词:正投影,平面图形.
6.三视图:⑴.主视图(由前向后看);⑵.俯视图(由上望下看);⑶.左视图(由左往右看).
7.画三视图的原则:
⑴.三视图摆放的位置原则(见右标示位置):
⑵.大小原则:长对正,高平齐,宽相等;
⑶.线条的虚实原则:可见实,遮挡虚.即看得见的轮廓线用实线,看不见的轮廓线用虚线.
8.常见几何体的三视图:
9.三种图形的转化:三视图 立体图 展开图.
10.与三视图有关的计算:.三视图 →立体图形→.侧面积、表面积、体积等等..
二.常见考点及题型例举
1. 投影
例1.作图:两根垂直于地面的木杆在路灯光线下的投影如图所示.⑴.确定路灯的位置;⑵.画出小强的投影.
作法:
⑴.通过两木棒的顶端点和投影的右端点分别画出投影线,两条投影线的交点就是路灯的位置;
⑵.通过路灯和小强的头顶画出投影线与地面的交点;
⑶.连接小强所在位置的底端点点与交点所得到的线段部分便是小强的影子位置.
例2.比例求高:如图,小华为了测楼房的高度,他请来同学帮忙,在阳光下测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米;已知小华的身高为1.6米,那么他所住的楼房的高度为 米.
略析:
太阳光线是平行光线,由于“在平行光线下,同一时刻物高与影长成正比”;
若设楼房高度为米,则有 ,解得: ,即小华
所住楼房的高度为48米.
例3.三角函数求高:如图(左图),当太阳光与地面成角时,直立于地面的玲玲测得自己的影长为 ,则玲玲的身高约为 .(精确到)
略析:
根据题意画出线条示意图(右图),⊿中,
, 影长 .
由锐角三角函数的定义可知:
∴ ;即玲玲的身高约为
例4.相似三角形求高:如图,为了测量学校旗杆的高度,小东用长为的竹竿做测量工具;移动竹竿,旗杆顶端的影子恰好落在地面同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为 .
分析:
本题把问题化归在两个相似三角形中的对应边成比例来解决.
若设旗杆高度为米,则有 ,解得:;
即旗杆的高度为.问题解决.
例5. 综合运用投影性质求高:为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
分析:
本题关键抓住灯杆高度是由两部分,上面一段和墙上投影相对应,下面
一段和地面投影相对应;上面一段利用与影长相等解决,下面一段利用成
比例关系解决.
略解:
根据题意画出示意图:代表灯杆,分别表示其在地上和墙上
的影子;代表小刚,代表其人影 .按如图方式连接和作平行线.
根据平行投影的的性质可知:米.
∵在太阳光(平行光线)下,同一时刻物高与影长成正比例.
∴ 即 解得:米.
∴米 即灯杆的高度为9.4米.
追踪练习:
1.如图,晚上小亮在路灯下散步,他从向着路灯柱方向走到处,这一过程中他在该路灯灯光下的影子 ( )
A.逐渐变短 B.逐渐变长 C.先变短后变长 D.先变长后变短
2.如图所示,杆在地面上的投影分别是,则下列判断正确的是 ( )
A. B.
C. D.以上三种都有可能
3.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球
在地面上的投影长是,则皮球的直径为 ( )
A. B. C. D.
4.如图,一条线段在平面中的正投影为,,
则线段与平面的夹角为 ( )
A.45° B.30° C.60° D.以上均不对
5.如图是一束平行光线从教室窗户射入教室的平面示意图,测得光线与地
面所成的角,窗户的高在教室地面的影长米,窗户
的下檐到教室地面的距离米(三点共线),则窗户的高
为 ( )
A.米 B.3米 C.2米 D.1.5米
6. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点)
20米的处,则小明的影长为 .
7. 如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在
地面上形成阴影(正方形)示意图,已知方桌边长,桌面离地面
,灯泡为离地面,则地面上的阴影部分的面积为 .
8. 根据图中已知投影,试确定图中路灯灯泡的位置,并画出小英在灯光下的影子.
9.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的。你能确定此时路灯光源的位置吗?
10.已知,如图,和是直立在地面上的两根立柱,,某一时刻在阳光的投影.
⑴.请你在图中画出此时在阳光下的投影;
⑵.在测量的投影时,同时测量出在阳光下的投影长为,请你计算的长.
11.晚上,一个身高1.6米的人(见图中)站在路灯下,发现自己的影子(见图中)刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?
12.如图是一起吊重物的简单装置,是吊杆,当它倾斜时,将重物挂起,当它逐渐直立时,重物便能逐渐升高;如图⑴,在阳光下,当时,量得吊杆的影子长米,很快将吊杆直立(直立过程所需时间忽略不计);如图(2),与地面垂直时,量得吊杆 的影子长米,求吊杆的长(结果精确到1米).
13.为了解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼,已知地区冬天中午12时阳光从正南方照射,并且光线与水平线之间的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?(结果保留整数)( )
14.如图所示,点表示广场上的一站照明灯,若小丽到灯柱的距离为4.5米,照明灯到灯柱的距离为1.5米,小丽测得照明灯的仰角为55°,她的目高为1.6米,试求照明灯到地面的距离(结果精确到0.1米).
2.由物画图(三视图)
例1.(教材96页例1)画出下列图中基本几何体的三视图.
分析:
画几何体的三视图时,要注意从三个方面观察它们,注意“长对正,宽平齐,高相等.”注意看得见的轮廓线用实线,看不见的轮廓线用虚线.
解:画出各几何体的三视图
例2.(教材97页例2)画出下列所示支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
分析:
支架的形状是由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长
方体的上下、前后关系;图中箭头方向是正方向
解:画出支架的三视图.
追踪练习:
1.如左图, 由两个相同的小正方形和一个圆锥体组成的立体图形,光线从上面往下照射这个几何体,所得到的正投影是 ( )
2.如图所示的几何体的主视图是 ( )
3.如图所示的几何体的主视图是 ( )
4..用两个完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是 ( )
5.如左图是一个空心圆台(空心部分也是一个圆台状),则这个几何体的俯视图为 ( )
6.如图,请将正六棱柱的三视图名称分别填在相应的横线上:
7.如图是一个圆锥和圆柱的组合体,在此组合体的三视图中,既是中心对称
图形,又是轴对称图形的是它的 视图(填“主”或“俯”或“左”)
8.分别画出下列各图的三视图(图中箭头所指方向是主视方向):
3.由图想物.
例1.由三视图还原几何体:(教材98页例4)根据物体的三视图摸索物体的现状.
分析:
由主视图可知,物体正面是正五边形;由俯视图可知,由上向
下看物体是矩形的,且有一条棱(中间的实线)可见到,两条
棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且
有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱
柱现状的.
解:物体是五棱柱形状,如图所示.
例2.由三视图确定立方体的个数:由一些大小 相同的小正方体组成的
几何体三视图如图所示,那么组成这个几何体的小正方体的个数 ( )
A.7 B.6 C.5 D.4
分析:由主视图和俯视图可知,俯视图右边两个方格的位置上各放置了一
个正方体,所以在这两个方格里分别填入1(如图),由主视图和俯视图
又知,俯视图左边一列上两个方格每格上最多2个正方体;又左视图和俯
视图知,俯视图中左边一列下边一列方格中应该只有一个正方体,故应填
入数字1,上边应有2个正方体,故填入数字2;所以成这个几何体的小
正方体的个数是(个).
口诀:俯视打基主视盖,左视拆违不懈怠.
例3.由视图求几何体的表面积、侧面积和体积等:如图是一个几何体的二视图,求该几何体的体积.( 取,单位:)
分析:由二视图可还原出一个长、宽、高分别为30、25、40的
长方体上和一个底圆直径为20,高为32的圆柱体的组合体形状,
该几何体的体积就是两种立体图形的体积之和.
略解:根据题意可知该几何体一个长、宽、高分别为30、25、40
的长方体上和一个底圆直径为20,高为32的圆柱体的组合体.
4.三种图形的转化(三视图 立体图 展开图)
例.(教材99页例5)某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
解:由三视图可知,密封罐的现状是正六棱柱(见右图);密封罐的高为,店面正六边形的直径为,边长为,中间图是它的展开图.
结合上面的展开图示意图和分析图(左图)可知制作一个密封罐所需钢板的面积为:
追踪练习:
1.下列左图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的主视图为 ( )
2.一个几何体由一些大小相同的小正方体组成,如右图是它主视图和左视图,那么组成该几何体所需的正方体的个数最少为 ( )
A.7个 B.8个 C.9个 D.10个
3.一个几何体的三视图如图所示,则这个几何体是 ( )
4.一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是 ( )
A. B. C. D.
5.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的表面积为 ( )
A. B. C. D.
6. 如图是由许多相同的小正方体堆砌的几何体的主视图及左视
图,则要摆这样的几何体至少要 个正方体,最多需要
个小正方体.
7. 一个画家有14个边长为的正方体,他在地面上把它们摆成如
图所示的几何体,然后把露在外面的表面部分都涂上颜色,那么涂上
颜色部分的总面积为 .
8.由一些大小 相同的小正方体组成的几何体三视图如图所示,那么
组成这个几何体的小正方体的个数 .
9.下面是一些物体的三视图,请同学们描述出它们各自的形状.
10.下面是正方体组合图的俯视图,方格中代表的该位置的层数,请画出其正视图、左视图.
11.如图是一个若干个棱长相等的正方体构成的几何体的三视图.
⑴.请写出构成这个几何体的正方体的个数;
⑵.请根据图中的尺寸,计算出这个几何体的表面积.
12.如图是一个几何体的二视图,求这个几何体的体积?
13.如图是一几何体三视图,根据图中标示求这一几何体的体积和表面积.
赵化中学 郑宗平 2020.3.15编制整理
《投影与视图》常见考点例举
注:本复习以《投影与视图》的内容为主.
一.知识链接
1.投影的定义、投影线、投影面;
2.投影的分类:
⑴.平行投影(投影线互相平行,即平行光线):①.斜投影(投影线与投影面斜交);②.正投影(投影光线与投影面垂直);
⑵.中心投影(投影线集中一点,即点光源形成的).
3.正投影的性质:
注:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
4.平行投影与中心投影
的区别与联系
5.视图的定义关键词:正投影,平面图形.
6.三视图:⑴.主视图(由前向后看);⑵.俯视图(由上望下看);⑶.左视图(由左往右看).
7.画三视图的原则:
⑴.三视图摆放的位置原则(见右标示位置):
⑵.大小原则:长对正,高平齐,宽相等;
⑶.线条的虚实原则:可见实,遮挡虚.即看得见的轮廓线用实线,看不见的轮廓线用虚线.
8.常见几何体的三视图:
9.三种图形的转化:三视图 立体图 展开图.
10.与三视图有关的计算:.三视图 →立体图形→.侧面积、表面积、体积等等..
二.常见考点及题型例举
1. 投影
例1.作图:两根垂直于地面的木杆在路灯光线下的投影如图所示.⑴.确定路灯的位置;⑵.画出小强的投影.
作法:
⑴.通过两木棒的顶端点和投影的右端点分别画出投影线,两条投影线的交点就是路灯的位置;
⑵.通过路灯和小强的头顶画出投影线与地面的交点;
⑶.连接小强所在位置的底端点点与交点所得到的线段部分便是小强的影子位置.
例2.比例求高:如图,小华为了测楼房的高度,他请来同学帮忙,在阳光下测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米;已知小华的身高为1.6米,那么他所住的楼房的高度为 米.
略析:
太阳光线是平行光线,由于“在平行光线下,同一时刻物高与影长成正比”;
若设楼房高度为米,则有 ,解得: ,即小华
所住楼房的高度为48米.
例3.三角函数求高:如图(左图),当太阳光与地面成角时,直立于地面的玲玲测得自己的影长为 ,则玲玲的身高约为 .(精确到)
略析:
根据题意画出线条示意图(右图),⊿中,
, 影长 .
由锐角三角函数的定义可知:
∴ ;即玲玲的身高约为
例4.相似三角形求高:如图,为了测量学校旗杆的高度,小东用长为的竹竿做测量工具;移动竹竿,旗杆顶端的影子恰好落在地面同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为 .
分析:
本题把问题化归在两个相似三角形中的对应边成比例来解决.
若设旗杆高度为米,则有 ,解得:;
即旗杆的高度为.问题解决.
例5. 综合运用投影性质求高:为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
分析:
本题关键抓住灯杆高度是由两部分,上面一段和墙上投影相对应,下面
一段和地面投影相对应;上面一段利用与影长相等解决,下面一段利用成
比例关系解决.
略解:
根据题意画出示意图:代表灯杆,分别表示其在地上和墙上
的影子;代表小刚,代表其人影 .按如图方式连接和作平行线.
根据平行投影的的性质可知:米.
∵在太阳光(平行光线)下,同一时刻物高与影长成正比例.
∴ 即 解得:米.
∴米 即灯杆的高度为9.4米.
追踪练习:
1.如图,晚上小亮在路灯下散步,他从向着路灯柱方向走到处,这一过程中他在该路灯灯光下的影子 ( )
A.逐渐变短 B.逐渐变长 C.先变短后变长 D.先变长后变短
2.如图所示,杆在地面上的投影分别是,则下列判断正确的是 ( )
A. B.
C. D.以上三种都有可能
3.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球
在地面上的投影长是,则皮球的直径为 ( )
A. B. C. D.
4.如图,一条线段在平面中的正投影为,,
则线段与平面的夹角为 ( )
A.45° B.30° C.60° D.以上均不对
5.如图是一束平行光线从教室窗户射入教室的平面示意图,测得光线与地
面所成的角,窗户的高在教室地面的影长米,窗户
的下檐到教室地面的距离米(三点共线),则窗户的高
为 ( )
A.米 B.3米 C.2米 D.1.5米
6. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点)
20米的处,则小明的影长为 .
7. 如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在
地面上形成阴影(正方形)示意图,已知方桌边长,桌面离地面
,灯泡为离地面,则地面上的阴影部分的面积为 .
8. 根据图中已知投影,试确定图中路灯灯泡的位置,并画出小英在灯光下的影子.
9.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的。你能确定此时路灯光源的位置吗?
10.已知,如图,和是直立在地面上的两根立柱,,某一时刻在阳光的投影.
⑴.请你在图中画出此时在阳光下的投影;
⑵.在测量的投影时,同时测量出在阳光下的投影长为,请你计算的长.
11.晚上,一个身高1.6米的人(见图中)站在路灯下,发现自己的影子(见图中)刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?
12.如图是一起吊重物的简单装置,是吊杆,当它倾斜时,将重物挂起,当它逐渐直立时,重物便能逐渐升高;如图⑴,在阳光下,当时,量得吊杆的影子长米,很快将吊杆直立(直立过程所需时间忽略不计);如图(2),与地面垂直时,量得吊杆 的影子长米,求吊杆的长(结果精确到1米).
13.为了解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼,已知地区冬天中午12时阳光从正南方照射,并且光线与水平线之间的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?(结果保留整数)( )
14.如图所示,点表示广场上的一站照明灯,若小丽到灯柱的距离为4.5米,照明灯到灯柱的距离为1.5米,小丽测得照明灯的仰角为55°,她的目高为1.6米,试求照明灯到地面的距离(结果精确到0.1米).
2.由物画图(三视图)
例1.(教材96页例1)画出下列图中基本几何体的三视图.
分析:
画几何体的三视图时,要注意从三个方面观察它们,注意“长对正,宽平齐,高相等.”注意看得见的轮廓线用实线,看不见的轮廓线用虚线.
解:画出各几何体的三视图
例2.(教材97页例2)画出下列所示支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
分析:
支架的形状是由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长
方体的上下、前后关系;图中箭头方向是正方向
解:画出支架的三视图.
追踪练习:
1.如左图, 由两个相同的小正方形和一个圆锥体组成的立体图形,光线从上面往下照射这个几何体,所得到的正投影是 ( )
2.如图所示的几何体的主视图是 ( )
3.如图所示的几何体的主视图是 ( )
4..用两个完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是 ( )
5.如左图是一个空心圆台(空心部分也是一个圆台状),则这个几何体的俯视图为 ( )
6.如图,请将正六棱柱的三视图名称分别填在相应的横线上:
7.如图是一个圆锥和圆柱的组合体,在此组合体的三视图中,既是中心对称
图形,又是轴对称图形的是它的 视图(填“主”或“俯”或“左”)
8.分别画出下列各图的三视图(图中箭头所指方向是主视方向):
3.由图想物.
例1.由三视图还原几何体:(教材98页例4)根据物体的三视图摸索物体的现状.
分析:
由主视图可知,物体正面是正五边形;由俯视图可知,由上向
下看物体是矩形的,且有一条棱(中间的实线)可见到,两条
棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且
有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱
柱现状的.
解:物体是五棱柱形状,如图所示.
例2.由三视图确定立方体的个数:由一些大小 相同的小正方体组成的
几何体三视图如图所示,那么组成这个几何体的小正方体的个数 ( )
A.7 B.6 C.5 D.4
分析:由主视图和俯视图可知,俯视图右边两个方格的位置上各放置了一
个正方体,所以在这两个方格里分别填入1(如图),由主视图和俯视图
又知,俯视图左边一列上两个方格每格上最多2个正方体;又左视图和俯
视图知,俯视图中左边一列下边一列方格中应该只有一个正方体,故应填
入数字1,上边应有2个正方体,故填入数字2;所以成这个几何体的小
正方体的个数是(个).
口诀:俯视打基主视盖,左视拆违不懈怠.
例3.由视图求几何体的表面积、侧面积和体积等:如图是一个几何体的二视图,求该几何体的体积.( 取,单位:)
分析:由二视图可还原出一个长、宽、高分别为30、25、40的
长方体上和一个底圆直径为20,高为32的圆柱体的组合体形状,
该几何体的体积就是两种立体图形的体积之和.
略解:根据题意可知该几何体一个长、宽、高分别为30、25、40
的长方体上和一个底圆直径为20,高为32的圆柱体的组合体.
4.三种图形的转化(三视图 立体图 展开图)
例.(教材99页例5)某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
解:由三视图可知,密封罐的现状是正六棱柱(见右图);密封罐的高为,店面正六边形的直径为,边长为,中间图是它的展开图.
结合上面的展开图示意图和分析图(左图)可知制作一个密封罐所需钢板的面积为:
追踪练习:
1.下列左图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的主视图为 ( )
2.一个几何体由一些大小相同的小正方体组成,如右图是它主视图和左视图,那么组成该几何体所需的正方体的个数最少为 ( )
A.7个 B.8个 C.9个 D.10个
3.一个几何体的三视图如图所示,则这个几何体是 ( )
4.一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是 ( )
A. B. C. D.
5.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的表面积为 ( )
A. B. C. D.
6. 如图是由许多相同的小正方体堆砌的几何体的主视图及左视
图,则要摆这样的几何体至少要 个正方体,最多需要
个小正方体.
7. 一个画家有14个边长为的正方体,他在地面上把它们摆成如
图所示的几何体,然后把露在外面的表面部分都涂上颜色,那么涂上
颜色部分的总面积为 .
8.由一些大小 相同的小正方体组成的几何体三视图如图所示,那么
组成这个几何体的小正方体的个数 .
9.下面是一些物体的三视图,请同学们描述出它们各自的形状.
10.下面是正方体组合图的俯视图,方格中代表的该位置的层数,请画出其正视图、左视图.
11.如图是一个若干个棱长相等的正方体构成的几何体的三视图.
⑴.请写出构成这个几何体的正方体的个数;
⑵.请根据图中的尺寸,计算出这个几何体的表面积.
12.如图是一个几何体的二视图,求这个几何体的体积?
13.如图是一几何体三视图,根据图中标示求这一几何体的体积和表面积.
赵化中学 郑宗平 2020.3.15编制整理
