2020年广东省中考数学模拟试卷(一)-2020届广东九年级数学中考总复习课件 (共23张PPT)
文档属性
| 名称 | 2020年广东省中考数学模拟试卷(一)-2020届广东九年级数学中考总复习课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 688.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 07:28:03 | ||
图片预览







文档简介
(共23张PPT)
2020年广东中考数学模拟试卷(一)
一、选择题(本大题10小题,每题3分,共30分)
1. 2 020的倒数是( )
A. -2 020 B. 2 020 C.- D.
2. 下列计算正确的是( )
A. B. x8÷x2=x4
C. (2a)3=6a3 D. 3a3·2a2=6a6
3. 分解因式x2y-4y,结果正确的是( )
A. y(x2-4) B. y(x-2)2
C. y(x+2)2 D. y(x+2)(x-2)
D
D
A
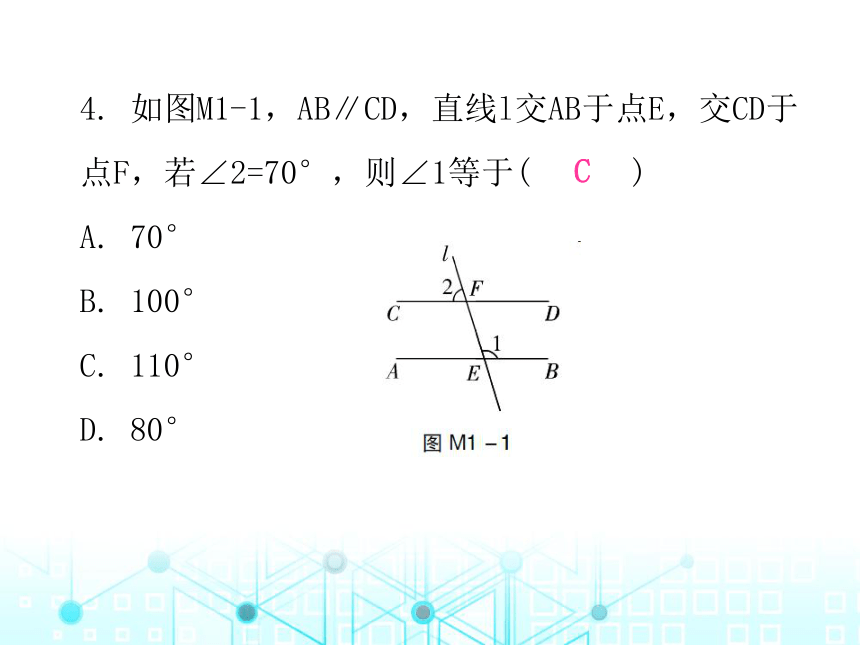
4. 如图M1-1,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
A. 70°
B. 100°
C. 110°
D. 80°
C
5. 下列图形中,不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 圆 D. 菱形
6. 数据3,4,7,4,8的中位数是( )
A. 3 B. 4 C. 7 D. 8
7. 一元二次方程x2-4x+5=0的两根之积是( )
A. 4 B. 5 C. 不存在 D. -5
8. 函数y= 中,自变量x的取值范围是( )
A. x>-1 B. x≥-1 C. x<-1 D. x≤1
A
B
C
B
9. 若两个相似正五边形的边长比为1∶10,则它们的面积比为( )
A. 1∶2 B. 1∶5 C. 1∶100 D. 1∶10
10. 如图M1-2,已知在正方形ABCD中,点O是对角线AC的中点,过点O的射线OM,ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA. 其中正确
的个数有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
C
C
二、填空题(本大题7小题,每题4分,共28分)
11. 已知∠A=80°,那么∠A的补角为____________度.
12. 分解因式:a3-4a=_____________________.
13. 据报道,2018年广东的人口超过1.27亿,将数1.27亿用科学记数法表示为____________.
14. 反比例函数y= 的图象经过点(2,3),则k=____________.
15. 已知一个正数的两个平方根分别为2m-6和3+m,则(-m)2 020的值为____________.
100
a(a+2)(a-2)
1.27×108
7
1
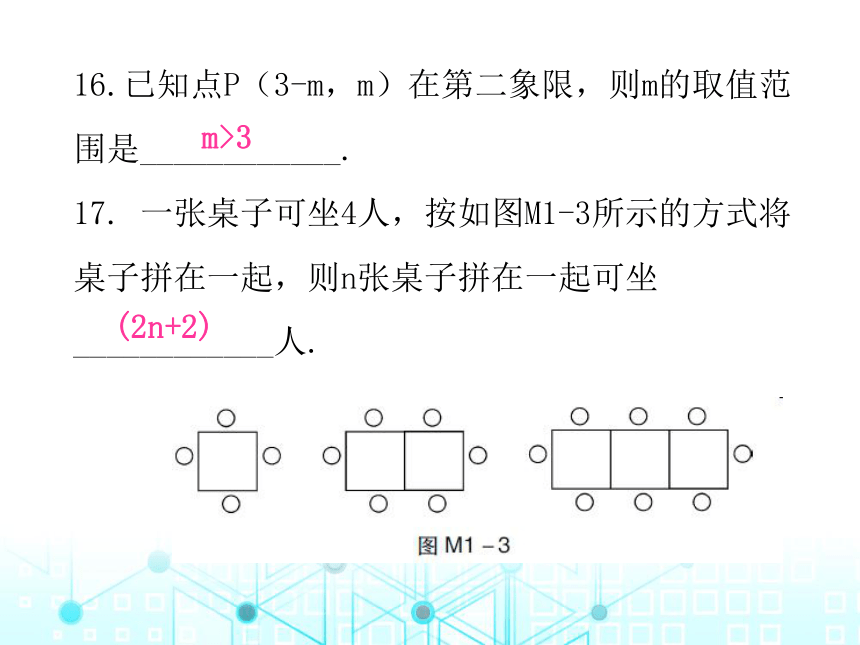
16.已知点P(3-m,m)在第二象限,则m的取值范围是____________.
17. 一张桌子可坐4人,按如图M1-3所示的方式将桌子拼在一起,则n张桌子拼在一起可坐 ____________人.
m>3
(2n+2)
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 计算: -6sin30°-(π+2 020)0+
19. 先化简,再求值:
其中x=2,y=
20. 如图M1-4,在∠CAD中,B为AC上一点.
(1)利用尺规作图:以点B为顶点,射线BC为一边,在∠CAD内部作∠CBE,使∠CBE=∠CAD(保留作图痕迹,不写作法);
(2)在(1)的条件下,EB与AD平行吗?
依据是什么?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图M1-5,把△ABC沿BC翻折得△DBC.
(1)连接AD,则BC与AD的位置关系是____________;
(2)不在原图中添加字母和线段,
只加一个条件使四边形ABDC是平行
四边形,写出添加的条件,并说明理由.
BC⊥AD
解:(2)添加的条件是AB=AC,理由如下.
由折叠知,∠ABC=∠DBC,∠ACB=∠DCB.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ACB=∠DBC=∠ABC=∠DCB.
∴AC∥BD,AB∥CD.
∴四边形ABDC是平行四边形.
22.据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15 m/s,在一条笔直公路BD的上方A处有一探测仪.如图M1-6,AD=24 m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2 s后到达C点,测得∠ACD=50°.
(1)求B,C之间的距离;
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,
结果精确到1 m)
23.重庆市某旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件.
(1)若要每天的利润不低于2 250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在五一节当天开展促销活动.若销售单价在(1)中的最低销售价的基础上再降低 m%,则日销售量可以在150件的基础上增加 m件,结果当天的销售额达到5 670元.要使销售量尽可能大,求出m的值.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图M1-7,在以线段AB为直径的⊙O上取一点C,连接AC,BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线
段AE,CB相交于点F,若BC=2,AC=4,
求线段EF的长.
25.如图M1-8,在Rt△ABC中,∠C=90°,AC=BC=4 cm,动点P从点C出发以1 cm/s的速度沿CA匀速运动,同时动点Q从点A出发以 cm/s的速度沿AB匀速运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为t s.
(1)当t为何值时,点B在线段PQ的垂直平分线上?
(2)是否存在某一时刻t,使△APQ是以PQ为腰的等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(3)以PC为边,往CB方向作正方形CPMN,
设四边形QNCP的面积为S,求S关于t的函数
关系式.
2020年广东中考数学模拟试卷(一)
一、选择题(本大题10小题,每题3分,共30分)
1. 2 020的倒数是( )
A. -2 020 B. 2 020 C.- D.
2. 下列计算正确的是( )
A. B. x8÷x2=x4
C. (2a)3=6a3 D. 3a3·2a2=6a6
3. 分解因式x2y-4y,结果正确的是( )
A. y(x2-4) B. y(x-2)2
C. y(x+2)2 D. y(x+2)(x-2)
D
D
A
4. 如图M1-1,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
A. 70°
B. 100°
C. 110°
D. 80°
C
5. 下列图形中,不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 圆 D. 菱形
6. 数据3,4,7,4,8的中位数是( )
A. 3 B. 4 C. 7 D. 8
7. 一元二次方程x2-4x+5=0的两根之积是( )
A. 4 B. 5 C. 不存在 D. -5
8. 函数y= 中,自变量x的取值范围是( )
A. x>-1 B. x≥-1 C. x<-1 D. x≤1
A
B
C
B
9. 若两个相似正五边形的边长比为1∶10,则它们的面积比为( )
A. 1∶2 B. 1∶5 C. 1∶100 D. 1∶10
10. 如图M1-2,已知在正方形ABCD中,点O是对角线AC的中点,过点O的射线OM,ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA. 其中正确
的个数有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
C
C
二、填空题(本大题7小题,每题4分,共28分)
11. 已知∠A=80°,那么∠A的补角为____________度.
12. 分解因式:a3-4a=_____________________.
13. 据报道,2018年广东的人口超过1.27亿,将数1.27亿用科学记数法表示为____________.
14. 反比例函数y= 的图象经过点(2,3),则k=____________.
15. 已知一个正数的两个平方根分别为2m-6和3+m,则(-m)2 020的值为____________.
100
a(a+2)(a-2)
1.27×108
7
1
16.已知点P(3-m,m)在第二象限,则m的取值范围是____________.
17. 一张桌子可坐4人,按如图M1-3所示的方式将桌子拼在一起,则n张桌子拼在一起可坐 ____________人.
m>3
(2n+2)
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 计算: -6sin30°-(π+2 020)0+
19. 先化简,再求值:
其中x=2,y=
20. 如图M1-4,在∠CAD中,B为AC上一点.
(1)利用尺规作图:以点B为顶点,射线BC为一边,在∠CAD内部作∠CBE,使∠CBE=∠CAD(保留作图痕迹,不写作法);
(2)在(1)的条件下,EB与AD平行吗?
依据是什么?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图M1-5,把△ABC沿BC翻折得△DBC.
(1)连接AD,则BC与AD的位置关系是____________;
(2)不在原图中添加字母和线段,
只加一个条件使四边形ABDC是平行
四边形,写出添加的条件,并说明理由.
BC⊥AD
解:(2)添加的条件是AB=AC,理由如下.
由折叠知,∠ABC=∠DBC,∠ACB=∠DCB.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ACB=∠DBC=∠ABC=∠DCB.
∴AC∥BD,AB∥CD.
∴四边形ABDC是平行四边形.
22.据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15 m/s,在一条笔直公路BD的上方A处有一探测仪.如图M1-6,AD=24 m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2 s后到达C点,测得∠ACD=50°.
(1)求B,C之间的距离;
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,
结果精确到1 m)
23.重庆市某旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件.
(1)若要每天的利润不低于2 250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在五一节当天开展促销活动.若销售单价在(1)中的最低销售价的基础上再降低 m%,则日销售量可以在150件的基础上增加 m件,结果当天的销售额达到5 670元.要使销售量尽可能大,求出m的值.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图M1-7,在以线段AB为直径的⊙O上取一点C,连接AC,BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线
段AE,CB相交于点F,若BC=2,AC=4,
求线段EF的长.
25.如图M1-8,在Rt△ABC中,∠C=90°,AC=BC=4 cm,动点P从点C出发以1 cm/s的速度沿CA匀速运动,同时动点Q从点A出发以 cm/s的速度沿AB匀速运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为t s.
(1)当t为何值时,点B在线段PQ的垂直平分线上?
(2)是否存在某一时刻t,使△APQ是以PQ为腰的等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(3)以PC为边,往CB方向作正方形CPMN,
设四边形QNCP的面积为S,求S关于t的函数
关系式.
同课章节目录
