2020年广东省中考数学模拟试卷(二)-2020届广东九年级数学中考总复习课件 (共26张PPT)
文档属性
| 名称 | 2020年广东省中考数学模拟试卷(二)-2020届广东九年级数学中考总复习课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 07:31:09 | ||
图片预览





文档简介
(共26张PPT)
2020年广东省中考数学模拟试卷(二)
一、选择题(本大题10小题,每小题3分,共30分)
1.4的算术平方根是( )
A.± B. C.±2 D.2
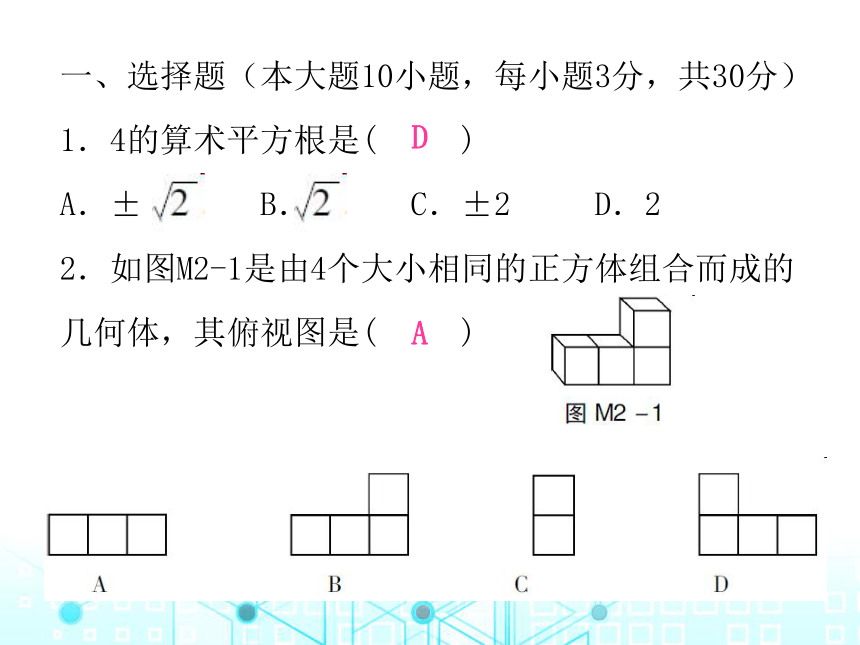
2.如图M2-1是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
D
A
3.PM2.5是指大气中直径不大于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A.2.5×105 B.2.5×10
C.2.5×10-5 D.2.5×10-6
4.某校“环保小组”的5名同学在一次活动中捡废弃塑料袋的个数分别是:4,6,9,6,10,这组数据的中位数、众数分别为( )
A.9,6 B.6,9 C .6,6 D .9,10
5.若一个正多边形的一个内角等于150°,则这个正多边形的边数是( )
A.9 B.10 C.11 D.12
D
C
D
6.不等式组 的解集是( )
A.x>1 B.-3<x<1 C.x>-3 D.无解
B
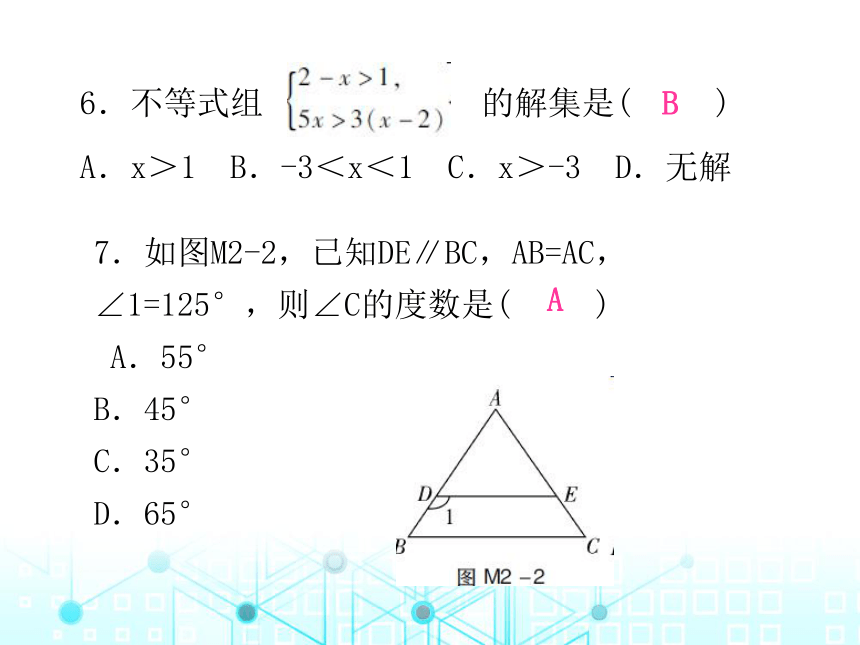
7.如图M2-2,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
A.55°
B.45°
C.35°
D.65°
A
8.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )
A.m≥-1 B.m>-1 C.m≤-1 D.m<-1
9.下列所述的图形中,既是轴对称图形,又是中心对称图形的是( )
A.平行四边形 B.等腰直角三角形
C.菱形 D.正五边形
A
C
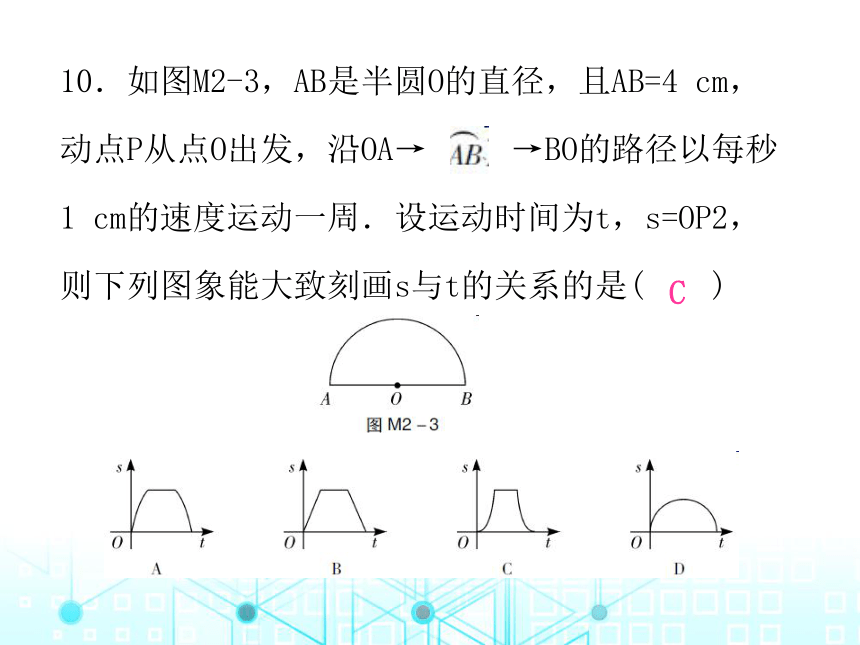
10.如图M2-3,AB是半圆O的直径,且AB=4 cm,动点P从点O出发,沿OA→ →BO的路径以每秒1 cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
C
二、填空题(本大题7小题,每小题4分,共28分)
11.函数y= 中自变量x的取值范围是____________.
12. 分解因式:2x2-4xy+2y2=____________.
13.已知代数式x+2y+1的值是6,则代数式3x+6y+1的值是____________.
14. (2019盐城)设x1,x2是方程x2-3x+2=0的两个根,则x1+x2-x1·x2=____________.
x≠-1
2(x-y)2
16
1
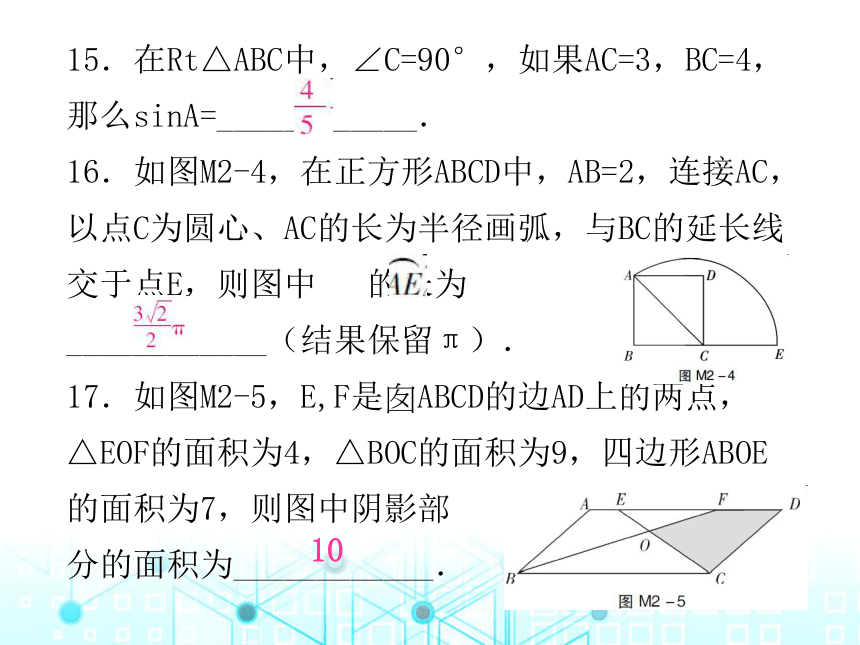
15.在Rt△ABC中,∠C=90°,如果AC=3,BC=4,那么sinA=____________.
16.如图M2-4,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC的长为半径画弧,与BC的延长线交于点E,则图中 的长为
____________(结果保留π).
17.如图M2-5,E,F是?ABCD的边AD上的两点,△EOF的面积为4,△BOC的面积为9,四边形ABOE的面积为7,则图中阴影部
分的面积为____________.
10
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.计算:(-5)0+|-3|-2sin60°+
19.先化简,再求值: 其中x=
20.如图M2-6,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD.
(1)过点D作AC的垂线,与AB交于点E(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,直接写出 的值.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图M2-7,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.
(1)求证:△BFD是等腰三角形;
(2)若BC=4,CD=2,求∠AFB的余弦值.
22.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
解:(1)设该市举办方应邀请x支球队参赛,依题意,得x(x-1)=30.
解得x1=6,x2=-5(不合题意,舍去).
答:该市举办方应邀请6支球队参赛.
(2)(10-4-2)×3+4×1+2×0=16(分).
答:该球队此次比赛的总积分为16分.
23.据某网站调查,2018年全国网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图如图M2-8.
根据以上信息解答下列问题:
(1)请补全条形统计图;
(2)如果某市约有300万人口,请你估计该市最关注教育问题的人数约为多少万人;
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,请用列表法或树状图法表示抽取的两人恰好是甲和乙的概率.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图M2-9,在平面直角坐标系中,直线y=x+m与x轴的交点为A(-4,0),与y轴的交点为B,线段AB的中点M在函数y= (k≠0)的图象上.
(1)求m,k的值;
(2)将线段AB向左平移n个单位长度(n>0)得到线段CD,A,M,B的对应点分别为C,N,D.
①当点D落在函数y= (x<0)的图象上时,求n的值;
②当MD≤MN时,结合函数的图象,直接写出n的取值范围.
25. (2019山西)综合与探究.
如图M2-10,抛物线y=ax2+bx+6经过点A(-2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的 时,求m的值;
(3)在(2)的条件下,若点M是x轴上一
动点,点N是抛物线上一动点,试判断是否
存在这样的点M,使得以点B,D,M,N为顶
点的四边形是平行四边形?若存在,请直
接写出点M的坐标;若不存在,请说明理由.
2020年广东省中考数学模拟试卷(二)
一、选择题(本大题10小题,每小题3分,共30分)
1.4的算术平方根是( )
A.± B. C.±2 D.2
2.如图M2-1是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
D
A
3.PM2.5是指大气中直径不大于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A.2.5×105 B.2.5×10
C.2.5×10-5 D.2.5×10-6
4.某校“环保小组”的5名同学在一次活动中捡废弃塑料袋的个数分别是:4,6,9,6,10,这组数据的中位数、众数分别为( )
A.9,6 B.6,9 C .6,6 D .9,10
5.若一个正多边形的一个内角等于150°,则这个正多边形的边数是( )
A.9 B.10 C.11 D.12
D
C
D
6.不等式组 的解集是( )
A.x>1 B.-3<x<1 C.x>-3 D.无解
B
7.如图M2-2,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
A.55°
B.45°
C.35°
D.65°
A
8.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )
A.m≥-1 B.m>-1 C.m≤-1 D.m<-1
9.下列所述的图形中,既是轴对称图形,又是中心对称图形的是( )
A.平行四边形 B.等腰直角三角形
C.菱形 D.正五边形
A
C
10.如图M2-3,AB是半圆O的直径,且AB=4 cm,动点P从点O出发,沿OA→ →BO的路径以每秒1 cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
C
二、填空题(本大题7小题,每小题4分,共28分)
11.函数y= 中自变量x的取值范围是____________.
12. 分解因式:2x2-4xy+2y2=____________.
13.已知代数式x+2y+1的值是6,则代数式3x+6y+1的值是____________.
14. (2019盐城)设x1,x2是方程x2-3x+2=0的两个根,则x1+x2-x1·x2=____________.
x≠-1
2(x-y)2
16
1
15.在Rt△ABC中,∠C=90°,如果AC=3,BC=4,那么sinA=____________.
16.如图M2-4,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC的长为半径画弧,与BC的延长线交于点E,则图中 的长为
____________(结果保留π).
17.如图M2-5,E,F是?ABCD的边AD上的两点,△EOF的面积为4,△BOC的面积为9,四边形ABOE的面积为7,则图中阴影部
分的面积为____________.
10
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.计算:(-5)0+|-3|-2sin60°+
19.先化简,再求值: 其中x=
20.如图M2-6,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD.
(1)过点D作AC的垂线,与AB交于点E(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,直接写出 的值.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图M2-7,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.
(1)求证:△BFD是等腰三角形;
(2)若BC=4,CD=2,求∠AFB的余弦值.
22.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
解:(1)设该市举办方应邀请x支球队参赛,依题意,得x(x-1)=30.
解得x1=6,x2=-5(不合题意,舍去).
答:该市举办方应邀请6支球队参赛.
(2)(10-4-2)×3+4×1+2×0=16(分).
答:该球队此次比赛的总积分为16分.
23.据某网站调查,2018年全国网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图如图M2-8.
根据以上信息解答下列问题:
(1)请补全条形统计图;
(2)如果某市约有300万人口,请你估计该市最关注教育问题的人数约为多少万人;
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,请用列表法或树状图法表示抽取的两人恰好是甲和乙的概率.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图M2-9,在平面直角坐标系中,直线y=x+m与x轴的交点为A(-4,0),与y轴的交点为B,线段AB的中点M在函数y= (k≠0)的图象上.
(1)求m,k的值;
(2)将线段AB向左平移n个单位长度(n>0)得到线段CD,A,M,B的对应点分别为C,N,D.
①当点D落在函数y= (x<0)的图象上时,求n的值;
②当MD≤MN时,结合函数的图象,直接写出n的取值范围.
25. (2019山西)综合与探究.
如图M2-10,抛物线y=ax2+bx+6经过点A(-2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的 时,求m的值;
(3)在(2)的条件下,若点M是x轴上一
动点,点N是抛物线上一动点,试判断是否
存在这样的点M,使得以点B,D,M,N为顶
点的四边形是平行四边形?若存在,请直
接写出点M的坐标;若不存在,请说明理由.
同课章节目录
