北师大版六年级下册《圆柱的体积一》课件(38张PPT)
文档属性
| 名称 | 北师大版六年级下册《圆柱的体积一》课件(38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
圆柱的体积(一)
北师大版六年级下册第一单元
导
语
同学们,通过这一节课的学习,我们将学会:
1.结合具体情境,感受物体体积的大小,发展空间观念。
2.经历“猜想与验证”探索圆柱体积计算方法的过程,体会“类比”的数学思想方法。
3.掌握圆柱体积的计算方法,能正确计算并解决相关简单的实际问题。
一个圆柱所占空间的大小,叫做这个圆柱的体积。
生 活 情 境
一个圆柱所占空间的大小,叫做这个圆柱的体积。
一个圆柱形容器所能容纳物体的体积,叫做这个圆柱形容器的容积。
体积和容积到底有什么区别呢?
(从外部测量)
(从内部测量)
?
长方体、正方体的体积都等于“底面积X高”。
我猜想圆柱的体积也可能等于“底面积X高”。
个 别 探 究
从叠硬币来看,可以用底面积乘高来计算这个圆柱的体积。
协 作 建 构
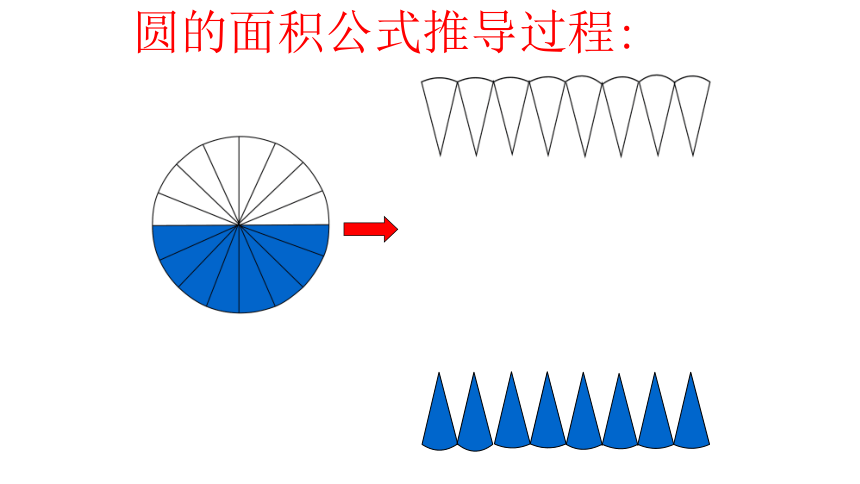
圆的面积公式推导过程:
思考以下几个问题:
1、切拼后,将圆柱拼成了我们学过的哪一种立体图形?
2、拼成的立体图形与原来圆柱相比,什么变了?什么没变?
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
长方体的体积
圆柱的体积
=
拼成的长方体与原来的圆柱有什么关系?
底面积
底面积
X
X
高
高
=
=
=
=
V = S X h
1、计算下面圆柱的体积。
= 60×4
= 240(cm3)
V=πr2 h
?V=π(d÷2)2 h ?
2、如果已知圆柱的底面半径r和高h,或者已知底面的直径d和高h,你可以写出圆柱体积的计算公式吗?
练 习 反 思
=3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
=3.14×(0.16×5)
V=πr2 h
=3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(ml)
答:一个杯子能装452.16毫升水。
=3.14×32×16
V=π(d÷2)2 h
从水杯里面量,水杯的底面直径是6cm,高是16cm。
课 堂 小 结
你学到了圆柱体积计算方法吗?
圆柱的体积(一)
北师大版六年级下册第一单元
导
语
同学们,通过这一节课的学习,我们将学会:
1.结合具体情境,感受物体体积的大小,发展空间观念。
2.经历“猜想与验证”探索圆柱体积计算方法的过程,体会“类比”的数学思想方法。
3.掌握圆柱体积的计算方法,能正确计算并解决相关简单的实际问题。
一个圆柱所占空间的大小,叫做这个圆柱的体积。
生 活 情 境
一个圆柱所占空间的大小,叫做这个圆柱的体积。
一个圆柱形容器所能容纳物体的体积,叫做这个圆柱形容器的容积。
体积和容积到底有什么区别呢?
(从外部测量)
(从内部测量)
?
长方体、正方体的体积都等于“底面积X高”。
我猜想圆柱的体积也可能等于“底面积X高”。
个 别 探 究
从叠硬币来看,可以用底面积乘高来计算这个圆柱的体积。
协 作 建 构
圆的面积公式推导过程:
思考以下几个问题:
1、切拼后,将圆柱拼成了我们学过的哪一种立体图形?
2、拼成的立体图形与原来圆柱相比,什么变了?什么没变?
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
长方体的体积
圆柱的体积
=
拼成的长方体与原来的圆柱有什么关系?
底面积
底面积
X
X
高
高
=
=
=
=
V = S X h
1、计算下面圆柱的体积。
= 60×4
= 240(cm3)
V=πr2 h
?V=π(d÷2)2 h ?
2、如果已知圆柱的底面半径r和高h,或者已知底面的直径d和高h,你可以写出圆柱体积的计算公式吗?
练 习 反 思
=3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
=3.14×(0.16×5)
V=πr2 h
=3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(ml)
答:一个杯子能装452.16毫升水。
=3.14×32×16
V=π(d÷2)2 h
从水杯里面量,水杯的底面直径是6cm,高是16cm。
课 堂 小 结
你学到了圆柱体积计算方法吗?
