北师大版六数下册 圆柱的体积(二)课件(14张PPT)
文档属性
| 名称 | 北师大版六数下册 圆柱的体积(二)课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 24.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
圆柱的体积(二)
进一步运用圆柱体积公式,解决一些实际问题。
体会不规则物体体积的计算方法,提高解决实际问题的能力。
导语
掌握圆柱体积的计算方法,并能正确计算圆柱的体积。
通过本课的学习,我们将学会:
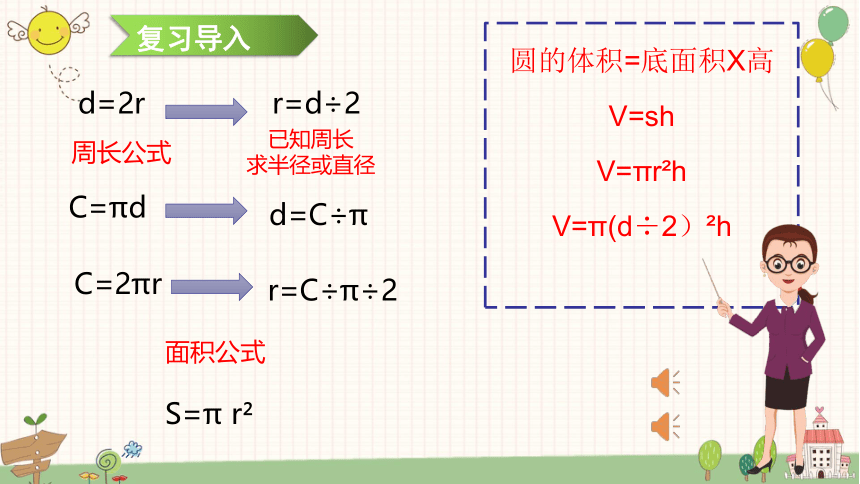
复习导入
已知周长
求半径或直径
面积公式
S=π r?
C=πd
d=C÷π
圆的体积=底面积X高V=sh
V=πr?h
V=π(d÷2)?h
周长公式
C=2πr
r=C÷π÷2
d=2r r=d÷2
活动一:生活情景
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
找数学信息 知道:圆柱的底面周长C=( )厘米,长(高)h=( )厘米,求圆柱的体积?
思路梳理
选用公式 先求底面半径 r=( )
再求底面积 S=( )
最后求体积 V=( )
列式计算
自主学习任务单
活动二:个别探究
活动二:个别探究
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
200cm
200cm
高
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
铁
活动二:个别探究
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
活动二:个别探究
答:这根金箍棒约重20千克。
解题思路:
(1)读题,找出已知信息;
(2)分析问题,理清思路;
(3)要注意单位是否一致;
(4)选用合适的公式,正确计算出体积。
自我评价:我能得
活动二:个别探究
活动三:练习检测
1、光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?
r=3.14÷3.14÷2=0.5(米)
v=sh
=3.14×0.52×4
=3.14×0.25×4
=3.14(立方米)
答:挖出了3.14立方米的土。
2、一个装满稻谷的粮囤,底面面积为2平方米,高为80厘米,每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?
V=sh
活动三
:练习检测
80厘米=0.8米
2×0.8=1.6(立方米)
1.6×700=1120(千克)
答:这个粮囤存放的稻谷的质量月约为1120 千克。
3、把一个铅球放入一个底面半径是8分米的圆柱形水桶中,水面的高度由4分米上升到6分米,这个铅球的体积是多少立方分米?
4分米
6分米
(上升?分米)
活动四:练习检测
3、把一个铅球放入一个底面半径是8分米的圆柱形水桶中,水面的高度由4分米上升到6分米,这个铅球的体积是多少立方分米?
活动三:练习检测
6-4=2(分米)
3.14×82×2
=3.14×64×2
=200.96×2
=401.92(立方分米)
答:这个铅球的体积是401.96立方分米。
课后作业
请你设计一个方案,测量并计算出1枚1元硬币的体积。
怎样才能准确地测量高呢?
圆柱的体积(二)
进一步运用圆柱体积公式,解决一些实际问题。
体会不规则物体体积的计算方法,提高解决实际问题的能力。
导语
掌握圆柱体积的计算方法,并能正确计算圆柱的体积。
通过本课的学习,我们将学会:
复习导入
已知周长
求半径或直径
面积公式
S=π r?
C=πd
d=C÷π
圆的体积=底面积X高V=sh
V=πr?h
V=π(d÷2)?h
周长公式
C=2πr
r=C÷π÷2
d=2r r=d÷2
活动一:生活情景
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
找数学信息 知道:圆柱的底面周长C=( )厘米,长(高)h=( )厘米,求圆柱的体积?
思路梳理
选用公式 先求底面半径 r=( )
再求底面积 S=( )
最后求体积 V=( )
列式计算
自主学习任务单
活动二:个别探究
活动二:个别探究
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
200cm
200cm
高
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
铁
活动二:个别探究
如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒重多少千克?
活动二:个别探究
答:这根金箍棒约重20千克。
解题思路:
(1)读题,找出已知信息;
(2)分析问题,理清思路;
(3)要注意单位是否一致;
(4)选用合适的公式,正确计算出体积。
自我评价:我能得
活动二:个别探究
活动三:练习检测
1、光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?
r=3.14÷3.14÷2=0.5(米)
v=sh
=3.14×0.52×4
=3.14×0.25×4
=3.14(立方米)
答:挖出了3.14立方米的土。
2、一个装满稻谷的粮囤,底面面积为2平方米,高为80厘米,每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?
V=sh
活动三
:练习检测
80厘米=0.8米
2×0.8=1.6(立方米)
1.6×700=1120(千克)
答:这个粮囤存放的稻谷的质量月约为1120 千克。
3、把一个铅球放入一个底面半径是8分米的圆柱形水桶中,水面的高度由4分米上升到6分米,这个铅球的体积是多少立方分米?
4分米
6分米
(上升?分米)
活动四:练习检测
3、把一个铅球放入一个底面半径是8分米的圆柱形水桶中,水面的高度由4分米上升到6分米,这个铅球的体积是多少立方分米?
活动三:练习检测
6-4=2(分米)
3.14×82×2
=3.14×64×2
=200.96×2
=401.92(立方分米)
答:这个铅球的体积是401.96立方分米。
课后作业
请你设计一个方案,测量并计算出1枚1元硬币的体积。
怎样才能准确地测量高呢?
