2020春湘教版八下数学2.5矩形教学课件(26张 2课时)
文档属性
| 名称 | 2020春湘教版八下数学2.5矩形教学课件(26张 2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 930.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览








文档简介
课件26张PPT。教学课件
数学 八年级下册 湘教版
第2章 四边形
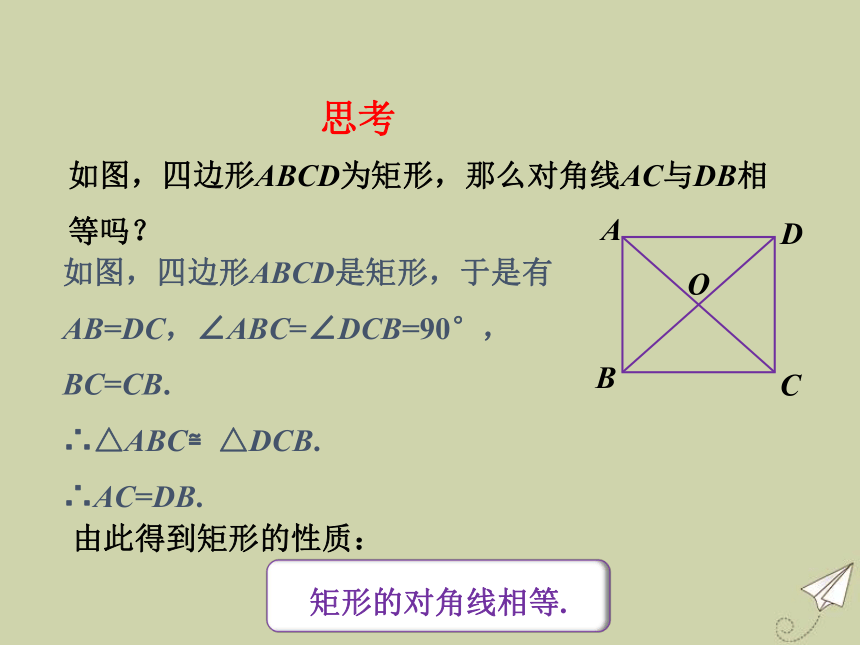
2.5 矩形2.5.1 矩形的性质在小学,我们初步认识了长方形,观察下图中的长方形,它是平行四边形吗?它有什么特点呢?观察我发现这些长方形的对边平行且相等,因此,它们是平行四边形.我发现这些四边形的四个角都是直角.在一个平行四边形中,只要有一个角是直角,那么其他三个角都是直角.矩形有一个角是直角的平行四边形叫作矩形,也称为长方形.矩形的四个角都是直角,对边相等,对角线互相平分.可以知道:由于矩形是平行四边形,因此矩形是中心对称图形,对角线的交点是它的对称中心.如图,四边形ABCD为矩形,那么对角线AC与DB相等吗?如图,四边形ABCD是矩形,于是有AB=DC,∠ABC=∠DCB=90°,BC=CB.
∴△ABC≌△DCB.
∴AC=DB.矩形的对角线相等.思考由此得到矩形的性质:【例1】如图,矩形ABCD的两条对角线AC,BD相交于点O,AC=4 cm,∠AOB=60°.求BC的长.画出一个矩形ABCD(如图),把它剪下来,怎么折叠能使矩形在折痕两旁的部分互相重合?满足这个要求的折叠方法有几种?由此猜测:矩形是轴对称图形吗?如果是,它有几条对称轴?你的猜测正确吗?由于AD∥BC,因此EF⊥AD.同理,直线EF是线段AD的垂直平分线.因此点B和点C关于直线EF对称,点A和点D关于直线EF对称,从而在关于直线EF的轴反射下,矩形ABCD的像与它自身重合,因此矩形ABCD是轴对称图形,EF是它的一条对称轴.类似地,过点O作直线MN⊥AB,且分别与边AB,DC相交于点M,N,则点M,N分别是边AB,DC的中点,直线MN是矩形ABCD的一条对称轴.矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.1.已知矩形的一条对角线的长度为2cm,两条对角线的一个夹角为60°,求矩形的各边长.2.如图,四边形ABCD为矩形,试利用矩形的性质证明:直角三角形ABC斜边AC上的中线BO等于斜边的一半.证明略.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.2.5.2 矩形的判定矩形的四个角都是直角,那么,四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?如图,四边形ABCD的四个角都是直角.由于“同旁内角互补,两直线平行”,因此AB∥DC,AD∥BC,从而四边形ABCD是平行四边形.所以□ABCD是矩形.由此得到四个角是直角的四边形是矩形.三个角是直角的四边形,容易知道另一个角是直角,所以:三个角是直角的四边形是
矩形.从“矩形的两条对角线相等且互相平分” 这一性质受到启发,你能画出一个对角线长度为4 cm的矩形吗?这样的矩形有多少个?过点O画两条线段AC,BD,使得OA=OC=2cm, OB=OD=2cm.连接AB,BC,CD,DA,则四边形ABCD是矩形,且它的对角线长度为4cm,如图.这样的矩形有无穷多个.如图,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等,上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?
证明 在□ABCD中,由于AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB.∴∠ABC=∠DCB.
又∵∠ABC+∠DCB=180°,∴∠ABC=90°.
∴□ABCD是矩形.对角线相等的平行四边形是矩形.由此得到矩形的判定定理:讨论对角线相等的四边形是矩形吗?对角线相等的四边形不一定是矩形,对角线相等且互相平分的四边形才是矩形.
如图,等腰梯形的对角线相等,但不是矩形.【例】如图,在□ABCD中,它的两条对角线相交于点O.
(1)如果□ABCD是矩形,试问:△OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中OB=OC,那么□ABCD是矩形吗?解 (1)∵□ABCD是矩形,
∴AC与DB相等且互相平分.
∴OB= 0.5DB= 0.5AC=OC.
∴△OBC是等腰三角形.
(2)∵△OBC是等腰三角形,其中OB=OC,
∴AC=2OC=2OB=BD.
∴□ABCD是矩形.1.如图,在四边形ABCD中,∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.证明:∵∠A=∠B=∠C=∠D,
且∠A+∠B+∠C+∠D=360°,∴∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是矩形.2.如图,在□ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=2,AC=4,求□ABCD的面积.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
数学 八年级下册 湘教版
第2章 四边形
2.5 矩形2.5.1 矩形的性质在小学,我们初步认识了长方形,观察下图中的长方形,它是平行四边形吗?它有什么特点呢?观察我发现这些长方形的对边平行且相等,因此,它们是平行四边形.我发现这些四边形的四个角都是直角.在一个平行四边形中,只要有一个角是直角,那么其他三个角都是直角.矩形有一个角是直角的平行四边形叫作矩形,也称为长方形.矩形的四个角都是直角,对边相等,对角线互相平分.可以知道:由于矩形是平行四边形,因此矩形是中心对称图形,对角线的交点是它的对称中心.如图,四边形ABCD为矩形,那么对角线AC与DB相等吗?如图,四边形ABCD是矩形,于是有AB=DC,∠ABC=∠DCB=90°,BC=CB.
∴△ABC≌△DCB.
∴AC=DB.矩形的对角线相等.思考由此得到矩形的性质:【例1】如图,矩形ABCD的两条对角线AC,BD相交于点O,AC=4 cm,∠AOB=60°.求BC的长.画出一个矩形ABCD(如图),把它剪下来,怎么折叠能使矩形在折痕两旁的部分互相重合?满足这个要求的折叠方法有几种?由此猜测:矩形是轴对称图形吗?如果是,它有几条对称轴?你的猜测正确吗?由于AD∥BC,因此EF⊥AD.同理,直线EF是线段AD的垂直平分线.因此点B和点C关于直线EF对称,点A和点D关于直线EF对称,从而在关于直线EF的轴反射下,矩形ABCD的像与它自身重合,因此矩形ABCD是轴对称图形,EF是它的一条对称轴.类似地,过点O作直线MN⊥AB,且分别与边AB,DC相交于点M,N,则点M,N分别是边AB,DC的中点,直线MN是矩形ABCD的一条对称轴.矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.1.已知矩形的一条对角线的长度为2cm,两条对角线的一个夹角为60°,求矩形的各边长.2.如图,四边形ABCD为矩形,试利用矩形的性质证明:直角三角形ABC斜边AC上的中线BO等于斜边的一半.证明略.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.2.5.2 矩形的判定矩形的四个角都是直角,那么,四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?如图,四边形ABCD的四个角都是直角.由于“同旁内角互补,两直线平行”,因此AB∥DC,AD∥BC,从而四边形ABCD是平行四边形.所以□ABCD是矩形.由此得到四个角是直角的四边形是矩形.三个角是直角的四边形,容易知道另一个角是直角,所以:三个角是直角的四边形是
矩形.从“矩形的两条对角线相等且互相平分” 这一性质受到启发,你能画出一个对角线长度为4 cm的矩形吗?这样的矩形有多少个?过点O画两条线段AC,BD,使得OA=OC=2cm, OB=OD=2cm.连接AB,BC,CD,DA,则四边形ABCD是矩形,且它的对角线长度为4cm,如图.这样的矩形有无穷多个.如图,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等,上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?
证明 在□ABCD中,由于AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB.∴∠ABC=∠DCB.
又∵∠ABC+∠DCB=180°,∴∠ABC=90°.
∴□ABCD是矩形.对角线相等的平行四边形是矩形.由此得到矩形的判定定理:讨论对角线相等的四边形是矩形吗?对角线相等的四边形不一定是矩形,对角线相等且互相平分的四边形才是矩形.
如图,等腰梯形的对角线相等,但不是矩形.【例】如图,在□ABCD中,它的两条对角线相交于点O.
(1)如果□ABCD是矩形,试问:△OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中OB=OC,那么□ABCD是矩形吗?解 (1)∵□ABCD是矩形,
∴AC与DB相等且互相平分.
∴OB= 0.5DB= 0.5AC=OC.
∴△OBC是等腰三角形.
(2)∵△OBC是等腰三角形,其中OB=OC,
∴AC=2OC=2OB=BD.
∴□ABCD是矩形.1.如图,在四边形ABCD中,∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.证明:∵∠A=∠B=∠C=∠D,
且∠A+∠B+∠C+∠D=360°,∴∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是矩形.2.如图,在□ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=2,AC=4,求□ABCD的面积.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
