人教版必修2第七章动能和动能定理的复习 (共30张ppt)
文档属性
| 名称 | 人教版必修2第七章动能和动能定理的复习 (共30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-23 20:49:27 | ||
图片预览











文档简介
(共30张PPT)
第七章 机械能守恒定律
7.8 动能和动能定理的复习
1.表达式:Ek=_______;
2.标矢性:动能是 量,只有 ,没有方向;
3.物体动能的变化量是指末动能减去初动能。
动能
1.关于物体的动能,下列说法正确的是
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化越大,其动能的变化一定越大
√
复习回顾:
标
大小
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中 ;
2.表达式:W=_____________。
动能定理
2.物体沿直线运动的v-t图象如图所示,已知在第1 s内合力对物体做功为W,则
A.从第1 s末到第3 s末合力做功为4W
B.从第3 s末到第5 s末合力做功为-2W
C.从第5 s末到第7 s末合力做功为W
D.从第3 s末到第4 s末合力做功为-0.5W
复习回顾:
√
动能的变化
3. 一质量为1kg的物体被人用手由静止向上提升1m时,物体的速度为2m/s,取g=10m/s 2 ,下列说法正确的是
A.提升过程中手对物体做功 12J
B.提升过程中合外力对物体做功12J
C.提升过程中合外力对物体做功2J
D.提升过程中物体克服重力做功10J
解:由动能定理得
W合=
∴ W合 =2J
其中W合 =W手 +(- W克 )
∴ W手 =12J
物体克服重力做功W克 =mgh =10J
复习回顾:
√
√
√
外力的总功
末状态动能
初状态动能
(1)合外力做功;
(2)外力做功之和。
动能定理的理解和应用
1.动能定理中的物理量
3.实质:动能定理从能量变化的角度反映了力改变运动的状态时,在空间上的累积效果。
2.动能定理公式中“=”体现的三个关系
动能定理的理解和应用
√
动能定理的理解和应用
5.适用范围:既适用于恒力做功,也适用于变力做功;既适用于直线运动,也适用于曲线运动。
动能定理的理解和应用
例2. 质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,重力加速度为g,则从开始碰撞到弹簧被压缩至最短,物体克服弹簧弹力所做的功为
√
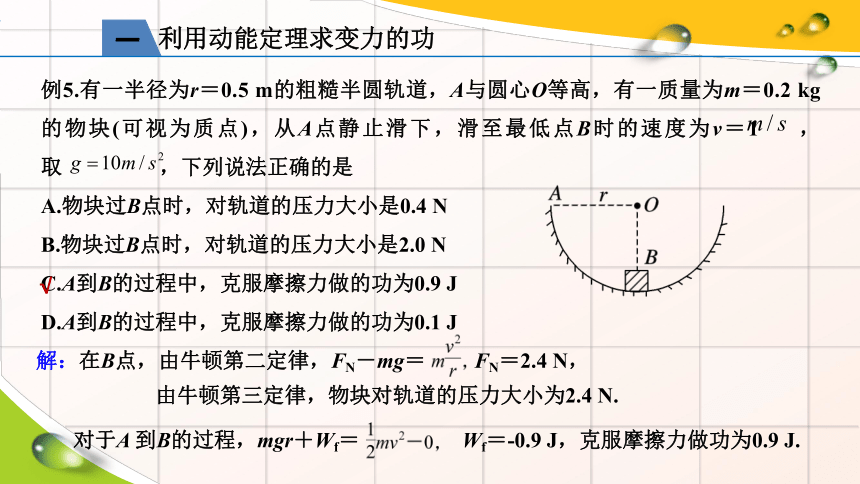
利用动能定理求变力的功
一
例3.一列货车的质量为5.0×105kg,在平直轨道以额定功率3000kw加速行驶,当速度由10m/s加速到所能达到的最大速度30m/s时,共用了2min,则这段时间内列车前进的距离是多少?
F0
f
f 恒定
S=1600m
S
利用动能定理求变力的功
一
例4.如图所示为一水平的转台,半径为R,一质量为m的滑块放在转台的边缘,已知滑块与转台间的动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,重力加速度为g.若转台的转速由零逐渐增大,当滑块在转台上刚好发生相对滑动时,转台对滑块所做的功为
√
利用动能定理求变力的功
一
例5.有一半径为r=0.5 m的粗糙半圆轨道,A与圆心O等高,有一质量为m=0.2 kg的物块(可视为质点),从A点静止滑下,滑至最低点B时的速度为v=1 ,取 ,下列说法正确的是
A.物块过B点时,对轨道的压力大小是0.4 N
B.物块过B点时,对轨道的压力大小是2.0 N
C.A到B的过程中,克服摩擦力做的功为0.9 J
D.A到B的过程中,克服摩擦力做的功为0.1 J
√
解:在B点,由牛顿第二定律,FN-mg= FN=2.4 N,
由牛顿第三定律,物块对轨道的压力大小为2.4 N.
对于A 到B的过程,mgr+Wf= Wf=-0.9 J,克服摩擦力做功为0.9 J.
利用动能定理求变力的功
一
利用动能定理求变力的功
一
利用动能定理求变力的功
一
1. 通常情况下,若问题涉及时间、加速度或过程的细节,要用牛顿运动定律解决;而曲线运动、变力做功等问题,一般要用动能定理解决。即使是恒力,当不涉及加速度和时间,并且是两个状态点的速度比较明确的情况,也应优先考虑动能定理。
2. 利用动能定理求变力的功是最常用的方法,当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
利用动能定理求变力的功
一
例7. 斜面倾角为α,长为L,AB段光滑,BC段粗糙,AB = , 质量为m的木块从斜面顶端无初速下滑,到达C端时速度刚好为零。求物体和BC段间的动摩擦因数μ。
B
A
C
L
α
解:以木块为对象,下滑全过程用动能定理:
初、末动能均为零;支持力不做功;
利用动能定理分析多过程问题
二
G
f
FN
由动能定理
例8.ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC段是与AB段和CD段都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止释放,沿轨道滑下,最后停在D点,A点和D点的位置如图1所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点回到A点,设滑块与轨道间的动摩擦因数为μ,重力加速度为g,则推力对滑块做的功等于
利用动能定理分析多过程问题
二
√
A点运动至D点,设克服摩擦力做功为WAD,
由动能定理得mgh-WAD=0,
D点回到A点,设克服摩擦力做功为WDA
滑块从D点被推回A点由动能定理,WF-mgh-WDA=0
WF=2mgh
由A点运动至D点,克服摩擦力做的功为
从D点到A点的过程克服摩擦力做的功为
x
=μmgx
=μmgx
利用动能定理分析多过程问题
二
例9.如图所示,质量为1kg的木块(可视为质点)静止在高1.2m的平台上,木块与平台间的动摩擦因数为0.2,用水平推力20N使木块产生位移3m时撤去,木块又滑行1m时飞出平台,求木块落地时速度的大小?
解:研究对象木块,研究过程从开始滑动到即将落地。
S1 + s2
设克服摩擦力做功为Wf
2
利用动能定理分析多过程问题
二
例10. ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出10 m,BC长1 m,AB和CD轨道光滑。一质量为1 kg的物体,从A点以4 m/s的速度沿轨道开始运动,经过BC后滑到高出C点10.3 m的D点时速度为零。求:(g取10 m/s2)
(1)物体与BC轨道间的动摩擦因数;
(2)物体第5次经过B点时的速度大小;
(3)物体最后停止的位置(距B点多少米)。
利用动能定理分析多过程问题
二
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
解: (1)由A到D,由动能定理得
解得μ=0.5
(3)分析整个过程,由动能定理得
解得s=21.6 m。来回运动了10次后,还有1.6 m,
故最后停止的位置与B点的距离为2 m-1.6 m=0.4 m。
利用动能定理分析多过程问题
二
一个物体的运动如果包含多个运动阶段,可以选择分段或全程应用动能定理。
(2)全程应用动能定理时,分析整个过程中出现过的各力的做功情况,分析每个力做的功,确定整个过程中合外力做的总功,然后确定整个过程的初、末动能,针对整个过程利用动能定理列式求解。
当题目不涉及加速度、时间等时,选择全程应用动能定理更简单,更方便。
(1)分段应用动能定理时,将复杂的过程分割成一个个子过程,对每个子过程的做功情况和初、末动能进行分析,然后针对每个子过程应用动能定理列式,然后联立求解。
利用动能定理分析多过程问题
二
例11.质量为m的小球(可视为质点)由静止自由下落d后,沿竖直面内的固定轨道ABC运动,AB是半径为d 的 光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点).小球恰能通过圆弧轨道的最高点C.重力加速度为g,求:
(1)小球运动到B处时对轨道的压力大小(可认为此时小球处在轨道AB上);
动能定理在平抛、圆周运动中的应用
三
(2)小球在BC运动过程中,摩擦力对小球做的功.
小球从B运动到C的过程:
根据牛顿第三定律:小球在B处对轨道的压力FN′= FN=5mg.
动能定理在平抛、圆周运动中的应用
三
例12.如图所示,一半径为R的半圆形轨道BC与一水平面相连,C为轨道的最高点,一质量为m的小球以初速度v0从圆形轨道B点进入,沿着圆形轨道运动并恰好通过最高点C,然后做平抛运动.求:
(1)小球平抛后落回水平面D点的位置距B点的距离;
(2)小球由B点沿着半圆轨道到达C点的过程中,克服轨道摩擦阻力做的功.
动能定理在平抛、圆周运动中的应用
三
解:(1)小球刚好通过C点,由牛顿第二定律
(2)小球由B点沿着半圆轨道到达C点,由动能定理
-mg·2R-Wf=
解得小球克服摩擦阻力做功
Wf=
小球做平抛运动,
小球平抛后落回水平面D点的位置距B点的距离
x=2R
动能定理在平抛、圆周运动中的应用
三
例13. 一可以看成质点的质量m=2 kg的小球以初速度v0沿光滑的水平桌面飞出后,恰好从A点沿切线方向进入圆弧轨道,BC为圆弧竖直直径,其中B为轨道的最低点,C为最高点且与水平桌面等高,圆弧AB对应的圆心角θ=53°,轨道半径R=0.5 m.已知sin 53°=0.8,cos 53°=0.6,不计空气阻力,g取10 m/s2.
(1)求小球的初速度v0的大小;
(2)若小球恰好能通过最高点C, 求在圆弧轨
道上摩擦力对小球做的功。
动能定理在平抛、圆周运动中的应用
三
代入数据解得Wf=-4 J.
得:v0=3 m/s.
解:(1)在A点由平抛运动规律得:
动能定理在平抛、圆周运动中的应用
三
(2)与竖直平面内的圆周运动相结合时,应特别注意隐藏的临界条件:
①可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为
vmin=0.
②不可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为
动能定理常与平抛运动、圆周运动相结合,解决这类问题要特别注意:
(1)与平抛运动相结合时,要注意应用运动的合成与分解的方法,求平抛运动的有关物理量.
动能定理在平抛、圆周运动中的应用
三
3.应用动能定理解题的一般步骤
(1)选取研究对象(通常是单个物体),明确它的运动过程;
(2)对研究对象进行受力分析,明确各力做功的情况,求出外力做功的代数和;
(3)明确物体在初、末状态的动能Ek1、Ek2;
(4)列出动能定理的方程W=Ek2-Ek1,结合其他必要的辅助方程求解并验算。
课堂小结
1.动能:Ek= ;标量;状态量。
2.动能定理:内容;
W= ;动能定理的理解。
4.动能定理在变力做功、曲线运动和多过程问题中的应用。
第七章 机械能守恒定律
7.8 动能和动能定理的复习
1.表达式:Ek=_______;
2.标矢性:动能是 量,只有 ,没有方向;
3.物体动能的变化量是指末动能减去初动能。
动能
1.关于物体的动能,下列说法正确的是
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化越大,其动能的变化一定越大
√
复习回顾:
标
大小
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中 ;
2.表达式:W=_____________。
动能定理
2.物体沿直线运动的v-t图象如图所示,已知在第1 s内合力对物体做功为W,则
A.从第1 s末到第3 s末合力做功为4W
B.从第3 s末到第5 s末合力做功为-2W
C.从第5 s末到第7 s末合力做功为W
D.从第3 s末到第4 s末合力做功为-0.5W
复习回顾:
√
动能的变化
3. 一质量为1kg的物体被人用手由静止向上提升1m时,物体的速度为2m/s,取g=10m/s 2 ,下列说法正确的是
A.提升过程中手对物体做功 12J
B.提升过程中合外力对物体做功12J
C.提升过程中合外力对物体做功2J
D.提升过程中物体克服重力做功10J
解:由动能定理得
W合=
∴ W合 =2J
其中W合 =W手 +(- W克 )
∴ W手 =12J
物体克服重力做功W克 =mgh =10J
复习回顾:
√
√
√
外力的总功
末状态动能
初状态动能
(1)合外力做功;
(2)外力做功之和。
动能定理的理解和应用
1.动能定理中的物理量
3.实质:动能定理从能量变化的角度反映了力改变运动的状态时,在空间上的累积效果。
2.动能定理公式中“=”体现的三个关系
动能定理的理解和应用
√
动能定理的理解和应用
5.适用范围:既适用于恒力做功,也适用于变力做功;既适用于直线运动,也适用于曲线运动。
动能定理的理解和应用
例2. 质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,重力加速度为g,则从开始碰撞到弹簧被压缩至最短,物体克服弹簧弹力所做的功为
√
利用动能定理求变力的功
一
例3.一列货车的质量为5.0×105kg,在平直轨道以额定功率3000kw加速行驶,当速度由10m/s加速到所能达到的最大速度30m/s时,共用了2min,则这段时间内列车前进的距离是多少?
F0
f
f 恒定
S=1600m
S
利用动能定理求变力的功
一
例4.如图所示为一水平的转台,半径为R,一质量为m的滑块放在转台的边缘,已知滑块与转台间的动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,重力加速度为g.若转台的转速由零逐渐增大,当滑块在转台上刚好发生相对滑动时,转台对滑块所做的功为
√
利用动能定理求变力的功
一
例5.有一半径为r=0.5 m的粗糙半圆轨道,A与圆心O等高,有一质量为m=0.2 kg的物块(可视为质点),从A点静止滑下,滑至最低点B时的速度为v=1 ,取 ,下列说法正确的是
A.物块过B点时,对轨道的压力大小是0.4 N
B.物块过B点时,对轨道的压力大小是2.0 N
C.A到B的过程中,克服摩擦力做的功为0.9 J
D.A到B的过程中,克服摩擦力做的功为0.1 J
√
解:在B点,由牛顿第二定律,FN-mg= FN=2.4 N,
由牛顿第三定律,物块对轨道的压力大小为2.4 N.
对于A 到B的过程,mgr+Wf= Wf=-0.9 J,克服摩擦力做功为0.9 J.
利用动能定理求变力的功
一
利用动能定理求变力的功
一
利用动能定理求变力的功
一
1. 通常情况下,若问题涉及时间、加速度或过程的细节,要用牛顿运动定律解决;而曲线运动、变力做功等问题,一般要用动能定理解决。即使是恒力,当不涉及加速度和时间,并且是两个状态点的速度比较明确的情况,也应优先考虑动能定理。
2. 利用动能定理求变力的功是最常用的方法,当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
利用动能定理求变力的功
一
例7. 斜面倾角为α,长为L,AB段光滑,BC段粗糙,AB = , 质量为m的木块从斜面顶端无初速下滑,到达C端时速度刚好为零。求物体和BC段间的动摩擦因数μ。
B
A
C
L
α
解:以木块为对象,下滑全过程用动能定理:
初、末动能均为零;支持力不做功;
利用动能定理分析多过程问题
二
G
f
FN
由动能定理
例8.ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC段是与AB段和CD段都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止释放,沿轨道滑下,最后停在D点,A点和D点的位置如图1所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点回到A点,设滑块与轨道间的动摩擦因数为μ,重力加速度为g,则推力对滑块做的功等于
利用动能定理分析多过程问题
二
√
A点运动至D点,设克服摩擦力做功为WAD,
由动能定理得mgh-WAD=0,
D点回到A点,设克服摩擦力做功为WDA
滑块从D点被推回A点由动能定理,WF-mgh-WDA=0
WF=2mgh
由A点运动至D点,克服摩擦力做的功为
从D点到A点的过程克服摩擦力做的功为
x
=μmgx
=μmgx
利用动能定理分析多过程问题
二
例9.如图所示,质量为1kg的木块(可视为质点)静止在高1.2m的平台上,木块与平台间的动摩擦因数为0.2,用水平推力20N使木块产生位移3m时撤去,木块又滑行1m时飞出平台,求木块落地时速度的大小?
解:研究对象木块,研究过程从开始滑动到即将落地。
S1 + s2
设克服摩擦力做功为Wf
2
利用动能定理分析多过程问题
二
例10. ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出10 m,BC长1 m,AB和CD轨道光滑。一质量为1 kg的物体,从A点以4 m/s的速度沿轨道开始运动,经过BC后滑到高出C点10.3 m的D点时速度为零。求:(g取10 m/s2)
(1)物体与BC轨道间的动摩擦因数;
(2)物体第5次经过B点时的速度大小;
(3)物体最后停止的位置(距B点多少米)。
利用动能定理分析多过程问题
二
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
解: (1)由A到D,由动能定理得
解得μ=0.5
(3)分析整个过程,由动能定理得
解得s=21.6 m。来回运动了10次后,还有1.6 m,
故最后停止的位置与B点的距离为2 m-1.6 m=0.4 m。
利用动能定理分析多过程问题
二
一个物体的运动如果包含多个运动阶段,可以选择分段或全程应用动能定理。
(2)全程应用动能定理时,分析整个过程中出现过的各力的做功情况,分析每个力做的功,确定整个过程中合外力做的总功,然后确定整个过程的初、末动能,针对整个过程利用动能定理列式求解。
当题目不涉及加速度、时间等时,选择全程应用动能定理更简单,更方便。
(1)分段应用动能定理时,将复杂的过程分割成一个个子过程,对每个子过程的做功情况和初、末动能进行分析,然后针对每个子过程应用动能定理列式,然后联立求解。
利用动能定理分析多过程问题
二
例11.质量为m的小球(可视为质点)由静止自由下落d后,沿竖直面内的固定轨道ABC运动,AB是半径为d 的 光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点).小球恰能通过圆弧轨道的最高点C.重力加速度为g,求:
(1)小球运动到B处时对轨道的压力大小(可认为此时小球处在轨道AB上);
动能定理在平抛、圆周运动中的应用
三
(2)小球在BC运动过程中,摩擦力对小球做的功.
小球从B运动到C的过程:
根据牛顿第三定律:小球在B处对轨道的压力FN′= FN=5mg.
动能定理在平抛、圆周运动中的应用
三
例12.如图所示,一半径为R的半圆形轨道BC与一水平面相连,C为轨道的最高点,一质量为m的小球以初速度v0从圆形轨道B点进入,沿着圆形轨道运动并恰好通过最高点C,然后做平抛运动.求:
(1)小球平抛后落回水平面D点的位置距B点的距离;
(2)小球由B点沿着半圆轨道到达C点的过程中,克服轨道摩擦阻力做的功.
动能定理在平抛、圆周运动中的应用
三
解:(1)小球刚好通过C点,由牛顿第二定律
(2)小球由B点沿着半圆轨道到达C点,由动能定理
-mg·2R-Wf=
解得小球克服摩擦阻力做功
Wf=
小球做平抛运动,
小球平抛后落回水平面D点的位置距B点的距离
x=2R
动能定理在平抛、圆周运动中的应用
三
例13. 一可以看成质点的质量m=2 kg的小球以初速度v0沿光滑的水平桌面飞出后,恰好从A点沿切线方向进入圆弧轨道,BC为圆弧竖直直径,其中B为轨道的最低点,C为最高点且与水平桌面等高,圆弧AB对应的圆心角θ=53°,轨道半径R=0.5 m.已知sin 53°=0.8,cos 53°=0.6,不计空气阻力,g取10 m/s2.
(1)求小球的初速度v0的大小;
(2)若小球恰好能通过最高点C, 求在圆弧轨
道上摩擦力对小球做的功。
动能定理在平抛、圆周运动中的应用
三
代入数据解得Wf=-4 J.
得:v0=3 m/s.
解:(1)在A点由平抛运动规律得:
动能定理在平抛、圆周运动中的应用
三
(2)与竖直平面内的圆周运动相结合时,应特别注意隐藏的临界条件:
①可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为
vmin=0.
②不可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为
动能定理常与平抛运动、圆周运动相结合,解决这类问题要特别注意:
(1)与平抛运动相结合时,要注意应用运动的合成与分解的方法,求平抛运动的有关物理量.
动能定理在平抛、圆周运动中的应用
三
3.应用动能定理解题的一般步骤
(1)选取研究对象(通常是单个物体),明确它的运动过程;
(2)对研究对象进行受力分析,明确各力做功的情况,求出外力做功的代数和;
(3)明确物体在初、末状态的动能Ek1、Ek2;
(4)列出动能定理的方程W=Ek2-Ek1,结合其他必要的辅助方程求解并验算。
课堂小结
1.动能:Ek= ;标量;状态量。
2.动能定理:内容;
W= ;动能定理的理解。
4.动能定理在变力做功、曲线运动和多过程问题中的应用。
