2020春苏科版八下数学9.4矩行菱形正方形教学课件(3课时 37张)
文档属性
| 名称 | 2020春苏科版八下数学9.4矩行菱形正方形教学课件(3课时 37张) |  | |
| 格式 | zip | ||
| 文件大小 | 541.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 08:11:57 | ||
图片预览









文档简介
课件37张PPT。教学课件数学 八年级下册 苏科版第9章 中心对称图形——
平行四边形9.4 矩形、菱形、正方形(第一课时)温故而知新矩形的定义有一个角是直角的平行四边形叫做矩形一个角是直角矩形的性质边角对角线矩形的对边平行且相等矩形的四个角都是直角矩形的 两条对角线相等且互相平分 1、我们知道,矩形的四个角都是直角.反过来,四个
角(或三个角)都是直角的四边形是矩形吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°.
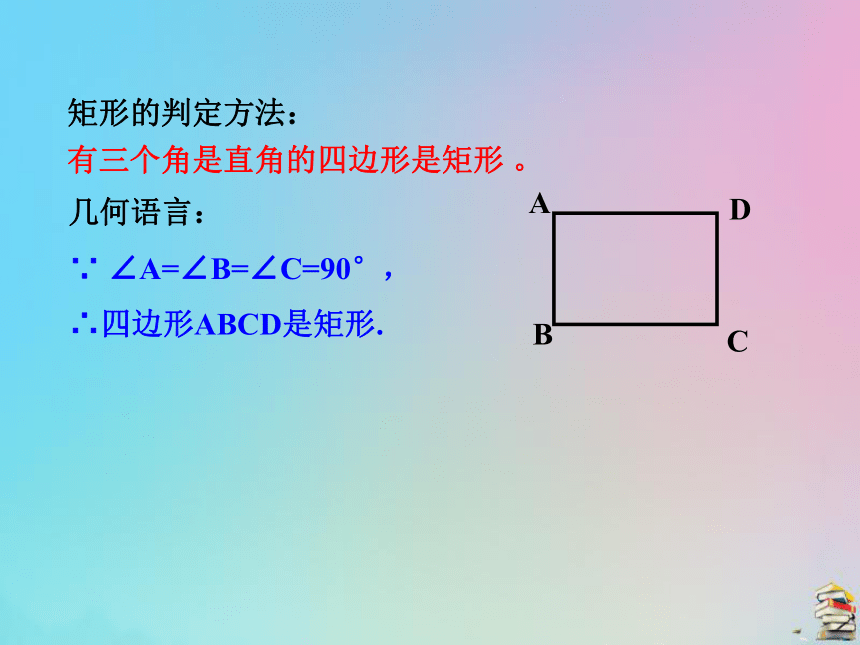
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°,∴ ∠A+∠B=180°,∴AD∥BC.同理可证:AB∥CD,∴四边形ABCD是平行四边形.又∵ ∠A=90°,∴四边形ABCD是矩形.矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.几何语言:情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线的长度,如果对角线的长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD,∴ △ABC≌ △DCB(SSS),∵ AB//CD,
∴ ∠ABC+∠DCB=180°, ∴ ∠ABC=∠DCB=90°.
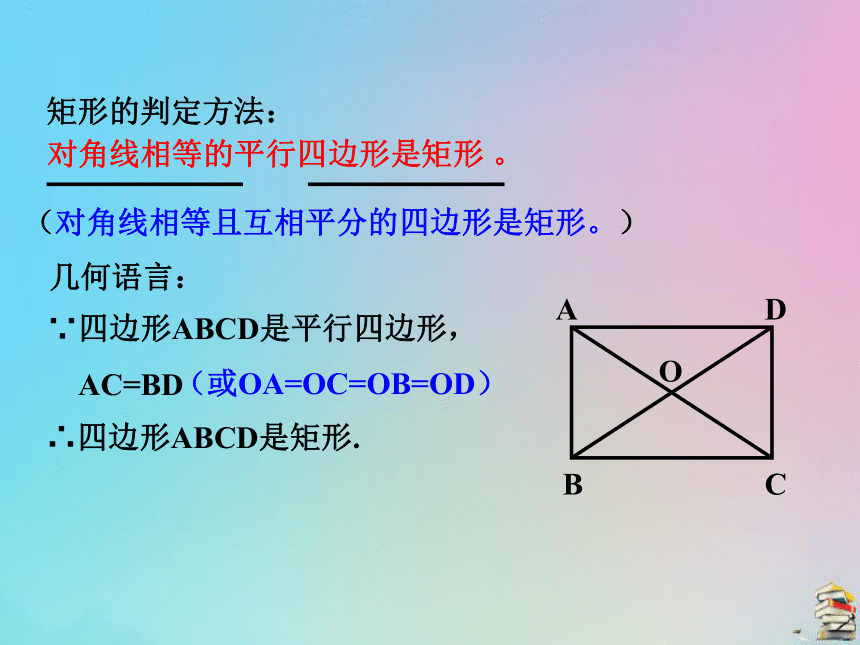
又∵ 四边形ABCD是平行四边形,∴四边形ABCD是矩形.∴ ∠ABC=∠DCB.对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形,
AC=BD∴四边形ABCD是矩形.(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)你能归纳出矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:1.有一个角是直角的平行四边形;
2.对角线相等的平行四边形;
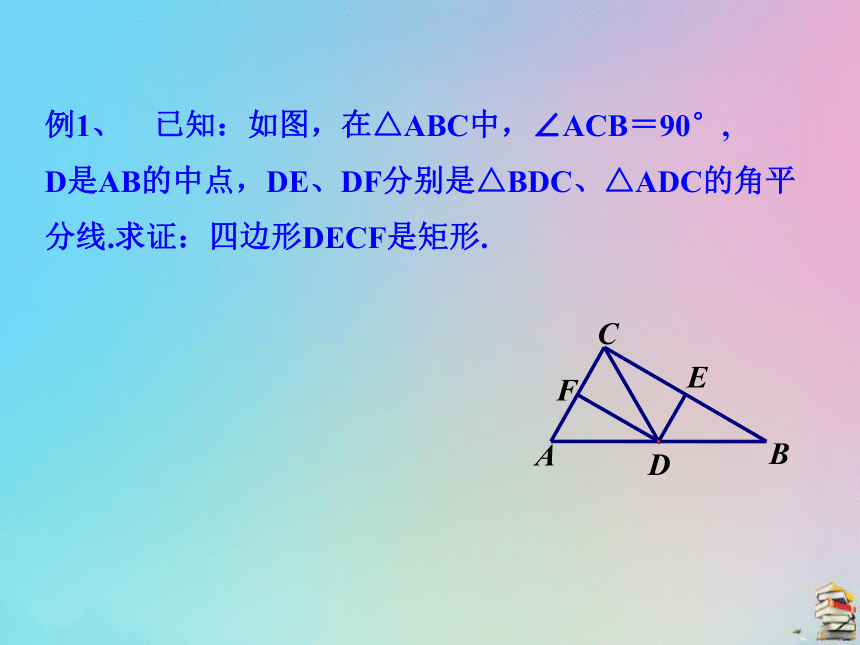
3.有三个角是直角的四边形.矩形. 判断矩形有哪几种方法?矩形的判定方法矩形. 矩形. 对于 四边形,满足哪些条件就可以得到矩形呢?任意平行例1、 已知:如图,在△ABC中,∠ACB=90°,
D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形.证明:
∵∠ACB=90°,D是AB的中点,
∴DC= AB=DA=DB.
∵ DC=DA,DF平分∠ADC,
∴DF⊥AC,
即∠DFC=90 °,
同理∠DEC=90 °,
∴四边形DECF是矩形(三个角是直角的四边形是矩形).例2 、如图,直线 l1∥l2 ,A、C是直线l1上任意的两点,AB⊥l2 ,CD⊥ l2 ,垂足分别为B、D,线段AB、CD相等吗?为什么?两条平行线之间的距离处处相等.解:由AB⊥l2 ,CD⊥ l2 ,可知
AB ∥ CD.
又因为l1∥l2 ,
所以四边形ABCD是矩形,
AB=CD.下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;1.已知:矩形ABCD的对角线AC、BD相交于点O,点E、F、G、H分别在OA、OB、OC、OD上,且AE=BF=CG=DH。求证:四边形EFGH是矩形.自学检测一:证明:∵四边形ABCD是平行四边形,
∴ AC=BD,
AO=CO= AC,BO=DO= BD,
∴AO=CO=BO=DO.
又∵ AE=BF=CG=DH,
∴ EO=FO=GO=HO,
∴四边形EFGH是平行四边形.
∵ EO=FO=GO=HO,∴ EG=FH.
∴四边形EFGH是矩形.2、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是 ;
(2)试用理由说明你的猜想.相等且互相平分课堂小结1.矩形的判定定理
(1)对角线相等的平行四边形是矩形。
(2)有三个角是直角的四边形是矩形。
2.矩形的性质在证明中的应用。
(对角线相等和四个角都是直角)
3.线段和角转移的方法。第二课时情境创设图片中有你熟悉的图形吗?这些图形有什么共同特征? 有一组邻边相等的平行四边形叫做菱形.∵在□ABCD中,AB=BC,
∴□ABCD是菱形.数学化认识符号语言:菱形的定义:菱形是一个特殊的平行四边形.菱形具有平行四边形的所有性质.菱形和平行四边形有什么关系?菱形既然是一个特殊的平行四边形,那么菱形还有哪些特殊的性质?探索活动一:菱形的四条边相等.∵四边形ABCD是菱形,
∴AB=BC=CD=DA.数学化认识菱形的性质:菱形的对角线互相垂直.符号语言:∵四边形ABCD是菱形,
∴AC⊥BD. 菱形是中心对称图形吗?是轴对称图形吗?如果是,请找出它的对称中心和对称轴.菱形既是中心对称图形,又是轴对称图形.探索活动三:菱形的对角相等;菱形的对角线互相垂直平分;从角看:从对角线看:从边看:菱形的对边平行;从对称性看:菱形既是轴对称图形,又是中心对称图形.菱形的性质:菱形的四条边相等;小结第三课时有一组邻边相等并且有一个角是直角的平行四边形叫做正方形. 数学化认识正方形的定义:符号语言:∵在□ABCD中,∠A=90°,AB=BC,
∴□ABCD是正方形.探索活动一:平行四边形、矩形、菱形、正方形的关系如何?正方形矩形菱形平行四边形说明:正方形具有矩形的性质,同时又具有菱形的性质.我们已经学习了平行四边形、矩形、菱形的性质,请在下表相应的空格内打“√”:探索活动二:√√√√√√√√√√√√√√√√√√√√√√√正方形的四条边都相等.∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°,
OA=OB=OC=OD,
AC=BD,AC⊥BD .数学化认识正方形的性质:符号语言:正方形的四个角都是直角.正方形的对角线相等且互相垂直平分. 矩形添加什么条件可成为正方形?菱形添加什么条件可成为正方形?你能归纳出判定正方形的条件吗?探索活动三:∵在矩形ABCD 中,AB=BC,
∴矩形ABCD是正方形.数学化认识正方形判定定理:符号语言:有一组邻边相等的矩形是正方形. 有一个角是直角的菱形是正方形.∵在菱形ABCD 中,∠A=90°,
∴矩形ABCD是正方形.下列说法正确吗?为什么?探索活动四:(1) 四条边都相等且有一个角是直角的四边形是正方形;(2) 有三个角是直角且有一组邻边相等的四边形是正方形;(3) 有三个角是直角且对角线互相垂直的四边形是正方形;(4) 对角线互相垂直平分且相等的四边形是正方形.例题讲解例1 、已知:如图,在正方形ABCD中,点A’、B’、C’、D’分别在AB、BC、CD、DA上,且AA’=BB’=CC’=DD’.求证:四边形A’B’C’D’ 是正方形.想一想:你还有其他证明方法吗?试一试.例2 、E是正方形ABCD边BC延长线上一点,且CE=AC.求∠E的大小.注:利用好正方形中特殊的角例题讲解例3 、在正方形ABCD中, 点E、F分别在AB、BC上,且AE=BF,AF与DE相交于点G.从所给的条件中,你能得出哪些结论?为什么?例题讲解
平行四边形9.4 矩形、菱形、正方形(第一课时)温故而知新矩形的定义有一个角是直角的平行四边形叫做矩形一个角是直角矩形的性质边角对角线矩形的对边平行且相等矩形的四个角都是直角矩形的 两条对角线相等且互相平分 1、我们知道,矩形的四个角都是直角.反过来,四个
角(或三个角)都是直角的四边形是矩形吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°,∴ ∠A+∠B=180°,∴AD∥BC.同理可证:AB∥CD,∴四边形ABCD是平行四边形.又∵ ∠A=90°,∴四边形ABCD是矩形.矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.几何语言:情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线的长度,如果对角线的长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD,∴ △ABC≌ △DCB(SSS),∵ AB//CD,
∴ ∠ABC+∠DCB=180°, ∴ ∠ABC=∠DCB=90°.
又∵ 四边形ABCD是平行四边形,∴四边形ABCD是矩形.∴ ∠ABC=∠DCB.对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形,
AC=BD∴四边形ABCD是矩形.(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)你能归纳出矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:1.有一个角是直角的平行四边形;
2.对角线相等的平行四边形;
3.有三个角是直角的四边形.矩形. 判断矩形有哪几种方法?矩形的判定方法矩形. 矩形. 对于 四边形,满足哪些条件就可以得到矩形呢?任意平行例1、 已知:如图,在△ABC中,∠ACB=90°,
D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形.证明:
∵∠ACB=90°,D是AB的中点,
∴DC= AB=DA=DB.
∵ DC=DA,DF平分∠ADC,
∴DF⊥AC,
即∠DFC=90 °,
同理∠DEC=90 °,
∴四边形DECF是矩形(三个角是直角的四边形是矩形).例2 、如图,直线 l1∥l2 ,A、C是直线l1上任意的两点,AB⊥l2 ,CD⊥ l2 ,垂足分别为B、D,线段AB、CD相等吗?为什么?两条平行线之间的距离处处相等.解:由AB⊥l2 ,CD⊥ l2 ,可知
AB ∥ CD.
又因为l1∥l2 ,
所以四边形ABCD是矩形,
AB=CD.下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;1.已知:矩形ABCD的对角线AC、BD相交于点O,点E、F、G、H分别在OA、OB、OC、OD上,且AE=BF=CG=DH。求证:四边形EFGH是矩形.自学检测一:证明:∵四边形ABCD是平行四边形,
∴ AC=BD,
AO=CO= AC,BO=DO= BD,
∴AO=CO=BO=DO.
又∵ AE=BF=CG=DH,
∴ EO=FO=GO=HO,
∴四边形EFGH是平行四边形.
∵ EO=FO=GO=HO,∴ EG=FH.
∴四边形EFGH是矩形.2、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是 ;
(2)试用理由说明你的猜想.相等且互相平分课堂小结1.矩形的判定定理
(1)对角线相等的平行四边形是矩形。
(2)有三个角是直角的四边形是矩形。
2.矩形的性质在证明中的应用。
(对角线相等和四个角都是直角)
3.线段和角转移的方法。第二课时情境创设图片中有你熟悉的图形吗?这些图形有什么共同特征? 有一组邻边相等的平行四边形叫做菱形.∵在□ABCD中,AB=BC,
∴□ABCD是菱形.数学化认识符号语言:菱形的定义:菱形是一个特殊的平行四边形.菱形具有平行四边形的所有性质.菱形和平行四边形有什么关系?菱形既然是一个特殊的平行四边形,那么菱形还有哪些特殊的性质?探索活动一:菱形的四条边相等.∵四边形ABCD是菱形,
∴AB=BC=CD=DA.数学化认识菱形的性质:菱形的对角线互相垂直.符号语言:∵四边形ABCD是菱形,
∴AC⊥BD. 菱形是中心对称图形吗?是轴对称图形吗?如果是,请找出它的对称中心和对称轴.菱形既是中心对称图形,又是轴对称图形.探索活动三:菱形的对角相等;菱形的对角线互相垂直平分;从角看:从对角线看:从边看:菱形的对边平行;从对称性看:菱形既是轴对称图形,又是中心对称图形.菱形的性质:菱形的四条边相等;小结第三课时有一组邻边相等并且有一个角是直角的平行四边形叫做正方形. 数学化认识正方形的定义:符号语言:∵在□ABCD中,∠A=90°,AB=BC,
∴□ABCD是正方形.探索活动一:平行四边形、矩形、菱形、正方形的关系如何?正方形矩形菱形平行四边形说明:正方形具有矩形的性质,同时又具有菱形的性质.我们已经学习了平行四边形、矩形、菱形的性质,请在下表相应的空格内打“√”:探索活动二:√√√√√√√√√√√√√√√√√√√√√√√正方形的四条边都相等.∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°,
OA=OB=OC=OD,
AC=BD,AC⊥BD .数学化认识正方形的性质:符号语言:正方形的四个角都是直角.正方形的对角线相等且互相垂直平分. 矩形添加什么条件可成为正方形?菱形添加什么条件可成为正方形?你能归纳出判定正方形的条件吗?探索活动三:∵在矩形ABCD 中,AB=BC,
∴矩形ABCD是正方形.数学化认识正方形判定定理:符号语言:有一组邻边相等的矩形是正方形. 有一个角是直角的菱形是正方形.∵在菱形ABCD 中,∠A=90°,
∴矩形ABCD是正方形.下列说法正确吗?为什么?探索活动四:(1) 四条边都相等且有一个角是直角的四边形是正方形;(2) 有三个角是直角且有一组邻边相等的四边形是正方形;(3) 有三个角是直角且对角线互相垂直的四边形是正方形;(4) 对角线互相垂直平分且相等的四边形是正方形.例题讲解例1 、已知:如图,在正方形ABCD中,点A’、B’、C’、D’分别在AB、BC、CD、DA上,且AA’=BB’=CC’=DD’.求证:四边形A’B’C’D’ 是正方形.想一想:你还有其他证明方法吗?试一试.例2 、E是正方形ABCD边BC延长线上一点,且CE=AC.求∠E的大小.注:利用好正方形中特殊的角例题讲解例3 、在正方形ABCD中, 点E、F分别在AB、BC上,且AE=BF,AF与DE相交于点G.从所给的条件中,你能得出哪些结论?为什么?例题讲解
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
