1.1.1 不等式的基本性质 课件 20张PPT
文档属性
| 名称 | 1.1.1 不等式的基本性质 课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 333.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 11:34:00 | ||
图片预览






文档简介
(共20张PPT)
选修4-5 不等式选讲
不等式的基本性质
O
x
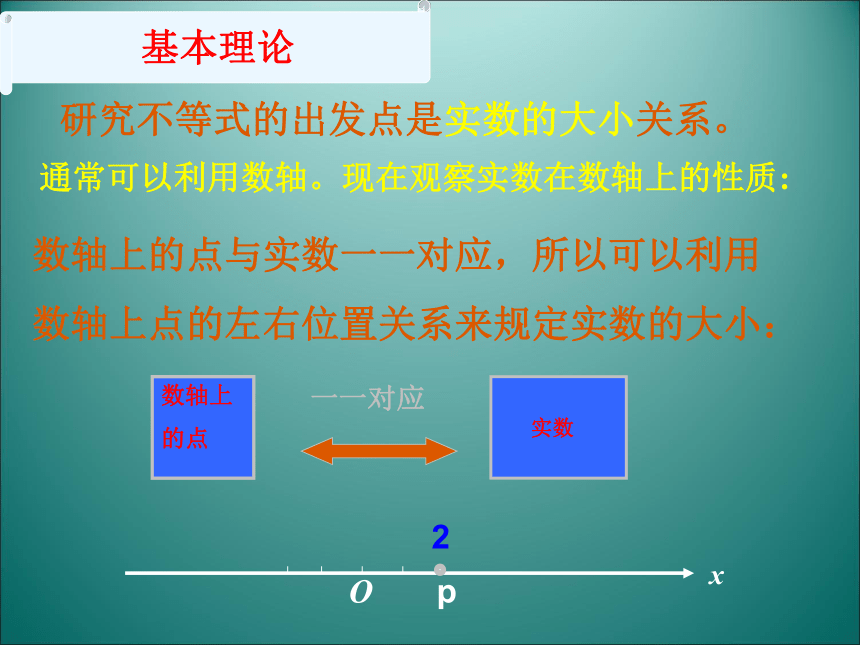
通常可以利用数轴。现在观察实数在数轴上的性质:
数轴上
的点
一一对应
p
2
基本理论
实数
研究不等式的出发点是实数的大小关系。
数轴上的点与实数一一对应,所以可以利用
数轴上点的左右位置关系来规定实数的大小:
设a,b是两个实数,它们在数轴上所对应的点分别为A,B那么,当点A在点B的左边时,ab
A
B
B
A
a
b
ax
b
a
a>b
x
对于任意两个实数a、b的大小都可以利用三个等价关系进行比较:
符号“ ”表示“等价于”,即可以互相推出。
作差比较法
理论依据
a-b>0 ?a>b;
a-b=0?a=b
a-b<0? a<b;
【思考】如何比较两个实数(代数式)的大小?
即利用作差法,判断其差的符号。
作差法
依 据 a-b>0 ?a>b
a-b=0?a=b
a-b<0? a<b
适用范围 若数(式)的大小不明显,作差后可化为积或商的形式。
步骤 (1)作差
(2)变形
(3)判断差的符号
(4)下结论
比较
解 :
>0
作差
变 形
定号
结论
作差比较大小
分四步进行
常见的变形手段是: 通分、因式分解或配方等;变形的结果是常数、若干个因式的积或完全平方式等.
<
<
作差
定号
结论
变形
课堂训练
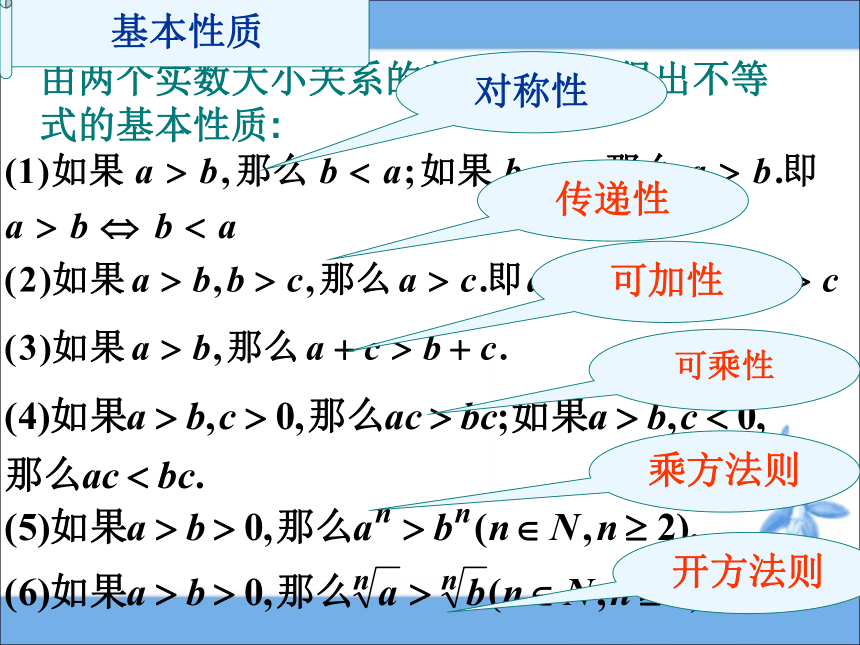
由两个实数大小关系的基本事实,得出不等式的基本性质:
对称性
传递性
可加性
可乘性
乘方法则
开方法则
基本性质
(同向可加性)
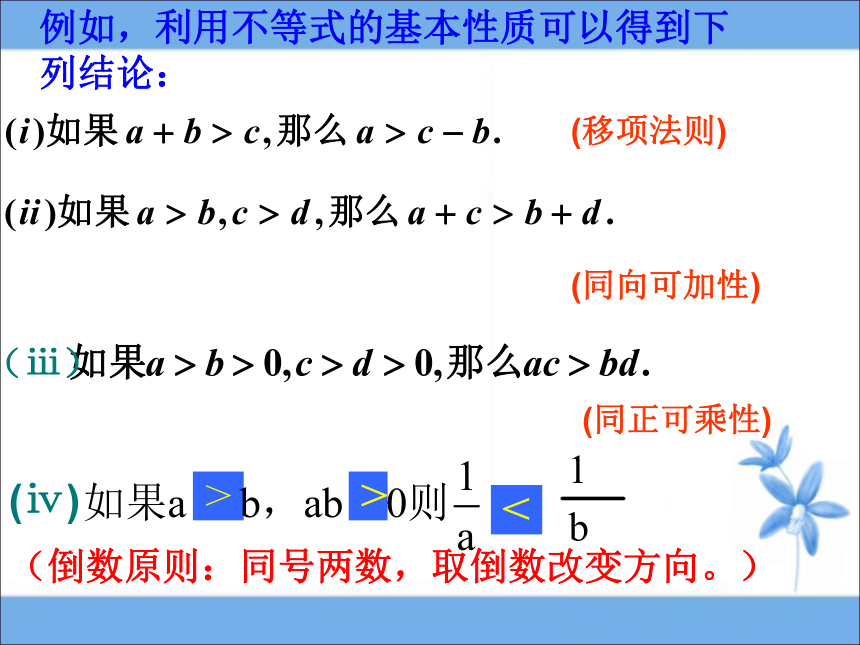
例如,利用不等式的基本性质可以得到下列结论:
(同正可乘性)
(移项法则)
>
(倒数原则:同号两数,取倒数改变方向。)
>
(ⅲ)
<
(ⅳ)
②
【练习】利用不等式性质判断对错
【注意】:一题多解——利用性质或特殊值法
(化繁为简)
不等式性质的应用——证明不等式
①
②
由①②可得
还有其他方法吗?
作商法
依据 a>0,b>0,且
a/b>1 ?a>b a/b=1 ?a=b
a/b<1 ? a<b
适用范围 同号两数比较大小,
或指数式之间比较
大小。
步骤 (1)作差
(2)变形
(3)判断商值与1的大小
(4)下结论
归纳小结:
不等式的性质是不等式这一章内容的基础,是不等式证明和解不等式的主要依据,因此应特别重视,应熟练掌握和运用不等式的几个性质和推论。
不等式的证明过程是应用不等式对已知不等式进行变形,从而得出要征的不等式,是证明不等式的常用方法之一。
bbba>c
a>c
ac>bc
ac>
>
a>b
设a,b∈R.试比较a2+b2-ab+1与a+b的大小.
作差法 作商法
依据 a-b>0 ?a>b
a-b=0?a=b
a-b<0? a<b a>0,b>0,
a/b>1 ?a>b a/b=1 ?a=b
a/b<1 ? a<b
适用范围 若数(式)的大小不明显,作差后可化为积或商的形式。 同号两数比较大小,或指数式之间比较大小。
步骤 (1)作差
(2)变形
(3)判断差值的符号
(4)下结论 (1)作差
(2)变形
(3)判断商值与1的大小
(4)下结论
作业:
1.填写不等式性质表格;
2.书本10页习题第3、4题
3. 练习册第3—5页页
选修4-5 不等式选讲
不等式的基本性质
O
x
通常可以利用数轴。现在观察实数在数轴上的性质:
数轴上
的点
一一对应
p
2
基本理论
实数
研究不等式的出发点是实数的大小关系。
数轴上的点与实数一一对应,所以可以利用
数轴上点的左右位置关系来规定实数的大小:
设a,b是两个实数,它们在数轴上所对应的点分别为A,B那么,当点A在点B的左边时,a
A
B
B
A
a
b
a
b
a
a>b
x
对于任意两个实数a、b的大小都可以利用三个等价关系进行比较:
符号“ ”表示“等价于”,即可以互相推出。
作差比较法
理论依据
a-b>0 ?a>b;
a-b=0?a=b
a-b<0? a<b;
【思考】如何比较两个实数(代数式)的大小?
即利用作差法,判断其差的符号。
作差法
依 据 a-b>0 ?a>b
a-b=0?a=b
a-b<0? a<b
适用范围 若数(式)的大小不明显,作差后可化为积或商的形式。
步骤 (1)作差
(2)变形
(3)判断差的符号
(4)下结论
比较
解 :
>0
作差
变 形
定号
结论
作差比较大小
分四步进行
常见的变形手段是: 通分、因式分解或配方等;变形的结果是常数、若干个因式的积或完全平方式等.
<
<
作差
定号
结论
变形
课堂训练
由两个实数大小关系的基本事实,得出不等式的基本性质:
对称性
传递性
可加性
可乘性
乘方法则
开方法则
基本性质
(同向可加性)
例如,利用不等式的基本性质可以得到下列结论:
(同正可乘性)
(移项法则)
>
(倒数原则:同号两数,取倒数改变方向。)
>
(ⅲ)
<
(ⅳ)
②
【练习】利用不等式性质判断对错
【注意】:一题多解——利用性质或特殊值法
(化繁为简)
不等式性质的应用——证明不等式
①
②
由①②可得
还有其他方法吗?
作商法
依据 a>0,b>0,且
a/b>1 ?a>b a/b=1 ?a=b
a/b<1 ? a<b
适用范围 同号两数比较大小,
或指数式之间比较
大小。
步骤 (1)作差
(2)变形
(3)判断商值与1的大小
(4)下结论
归纳小结:
不等式的性质是不等式这一章内容的基础,是不等式证明和解不等式的主要依据,因此应特别重视,应熟练掌握和运用不等式的几个性质和推论。
不等式的证明过程是应用不等式对已知不等式进行变形,从而得出要征的不等式,是证明不等式的常用方法之一。
bbba>c
a>c
ac>bc
ac
>
a>b
设a,b∈R.试比较a2+b2-ab+1与a+b的大小.
作差法 作商法
依据 a-b>0 ?a>b
a-b=0?a=b
a-b<0? a<b a>0,b>0,
a/b>1 ?a>b a/b=1 ?a=b
a/b<1 ? a<b
适用范围 若数(式)的大小不明显,作差后可化为积或商的形式。 同号两数比较大小,或指数式之间比较大小。
步骤 (1)作差
(2)变形
(3)判断差值的符号
(4)下结论 (1)作差
(2)变形
(3)判断商值与1的大小
(4)下结论
作业:
1.填写不等式性质表格;
2.书本10页习题第3、4题
3. 练习册第3—5页页
