1.1.3三个正数的算术-几何平均不等式 课件 23张PPT
文档属性
| 名称 | 1.1.3三个正数的算术-几何平均不等式 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 341.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 10:51:56 | ||
图片预览





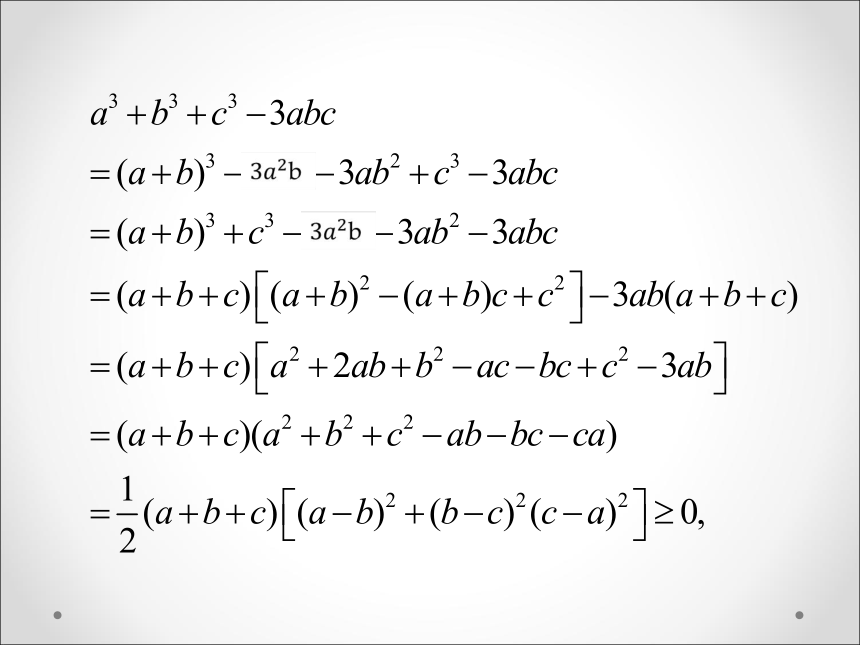



文档简介
(共23张PPT)
1.3 三个正数的算术---几何平均不等式
定理1.如果
,那么
(当且仅当
时取“=”号)
1.指出定理适用范围:
2.强调取“=”的条件:
定理2.如果
那么
是正数,
(当且仅当
时取“=”号)
注意:1.这个定理适用的范围:
2.语言表述:两个正数的算术平均数不小于它们的几何平均数。
利用算术平均数和几何平均数定理时一定要注意定理的条件:
一正;二定;三相等.
有一个条件达不到就不能取得最值.
基本不等式给出了两个正数的算术平均数与几何平均数的关系,这个不等式能否推广呢?例如,对于3个正数,会有怎样的不等式成立呢?
?
?
语言表述:三个正数的算术平均不小于它们的
几何平均。
定理3:
?
关于“平均数”的概念:
1.如果
则:
叫做这n个正数的算术平均数。
叫做这n个正数的几何平均数。
2.基本不等式:
≥
语言表述:n个正数的算术平均数不小于它们的几何平均数,当且仅当a1=a2=…=an时,等号成立.
例2:
解:
构造三个数相加等于定值.
解:
构造三个数相加等于定值.
例3将一块边长为a的正方形铁皮,剪去四个角(四
个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
解:
设剪去的小正方形的边长为
则其容积为 :
解:
(错解:原因是取不到等号)
正解:
求函数 的最小值.
下面解法是否正确?
解 :由 知 ,则
当且仅当
小结:利用三个正实数的基本不等式求最值时注意:
2、不能直接利用定理时,注意拆项、配项凑定值的技巧(拆项时常拆成两个相同项)。
1、一正、二定、三相等;
A、6 B、 C、9 D、12
( )
变式:
C
变式:
8
练习:
8
A、4 B、3 C、6 D、5
B
二、用基本不等式证明不等式
练习
1.3 三个正数的算术---几何平均不等式
定理1.如果
,那么
(当且仅当
时取“=”号)
1.指出定理适用范围:
2.强调取“=”的条件:
定理2.如果
那么
是正数,
(当且仅当
时取“=”号)
注意:1.这个定理适用的范围:
2.语言表述:两个正数的算术平均数不小于它们的几何平均数。
利用算术平均数和几何平均数定理时一定要注意定理的条件:
一正;二定;三相等.
有一个条件达不到就不能取得最值.
基本不等式给出了两个正数的算术平均数与几何平均数的关系,这个不等式能否推广呢?例如,对于3个正数,会有怎样的不等式成立呢?
?
?
语言表述:三个正数的算术平均不小于它们的
几何平均。
定理3:
?
关于“平均数”的概念:
1.如果
则:
叫做这n个正数的算术平均数。
叫做这n个正数的几何平均数。
2.基本不等式:
≥
语言表述:n个正数的算术平均数不小于它们的几何平均数,当且仅当a1=a2=…=an时,等号成立.
例2:
解:
构造三个数相加等于定值.
解:
构造三个数相加等于定值.
例3将一块边长为a的正方形铁皮,剪去四个角(四
个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
解:
设剪去的小正方形的边长为
则其容积为 :
解:
(错解:原因是取不到等号)
正解:
求函数 的最小值.
下面解法是否正确?
解 :由 知 ,则
当且仅当
小结:利用三个正实数的基本不等式求最值时注意:
2、不能直接利用定理时,注意拆项、配项凑定值的技巧(拆项时常拆成两个相同项)。
1、一正、二定、三相等;
A、6 B、 C、9 D、12
( )
变式:
C
变式:
8
练习:
8
A、4 B、3 C、6 D、5
B
二、用基本不等式证明不等式
练习
