1.1.2 基本不等式 课件 18张PPT
文档属性
| 名称 | 1.1.2 基本不等式 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 645.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
基本不等式(一)
数学史
三国时期吴国赵爽,绘制此图最早对勾股定理进行了证明
引入
A
D
B
C
E
F
G
H
b
a
A
B
C
D
E(FGH)
a
b
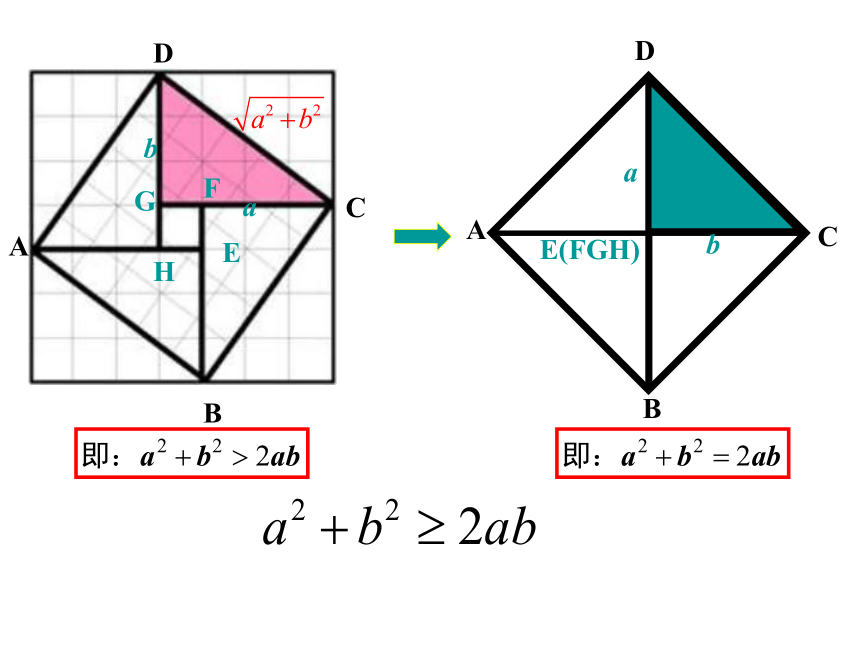
思考:你能给出对任意实数a,b,不等式 都成立的证明吗?
证明:(作差法)
证明重要不等式
一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立。
重要不等式:
①
②
③
≥
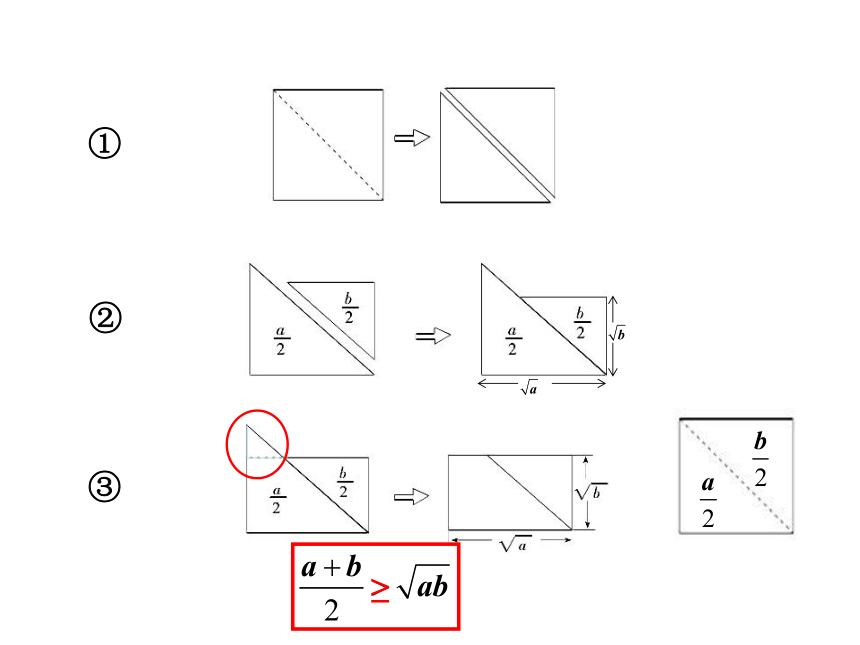
特别地,若a>0,b>0,则
≥
当且仅当a=b时取等号,这个不等式就叫做基本不等式.
在数学中,我们把 叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数;
定义基本不等式
文字语言:
两个正数的算术平均数不小于它们的几何平均数
从不同角度认识基本不等式
问题1:基本不等式 从数列的
角度,还可以怎么表述?
两个正数的等差中项不小于它们的等比中项
从不同角度认识基本不等式
A
B
C
E
a
b
O
D
几何意义:
证明:要证
只要证
①
要证②,只要证
②
要证③,只要证
③
显然, ④是成立的.当且仅当a=b时, ④中的等号成立.
分析法
思考:你还能给出基本不等式 的其他证明吗?
执果索因
证明基本不等式
④
问题3:你能否借助已证的重要不等式 ,分析基本不等式 的成立性呢?
证明基本不等式
解:如图设BC=x ,CD=y ,
则xy=100,
篱笆的长为2(x+y)m.
当且仅当 时,等号成立
因此,这个矩形的长、宽都为10m时,所用的篱笆最短,最短的篱笆是40m.
此时x=y=10.
x=y
A
B
D
C
例:(1)如图,用篱笆围成一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?
运用基本不等式求最值
因此,这个矩形的长、宽都为9m时,
菜园面积最大,最大面积是81m2
A
B
D
C
运用基本不等式求最值
例:(2)如图,用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?
知识方法小结
数学建模 数形结合
运用基本不等式求最值的条件:
一正、二定、三相等
布置作业
课堂作业:教材第100页习题A组第1,2题
课后作业:课后在网上查找基本不等式的其他代数几何证明方法,整理并相互交流。
思考:由基本不等式 出发,
你还能推导出哪些公式?
课后思考题
谢谢大家,敬请指导!
基本不等式(一)
数学史
三国时期吴国赵爽,绘制此图最早对勾股定理进行了证明
引入
A
D
B
C
E
F
G
H
b
a
A
B
C
D
E(FGH)
a
b
思考:你能给出对任意实数a,b,不等式 都成立的证明吗?
证明:(作差法)
证明重要不等式
一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立。
重要不等式:
①
②
③
≥
特别地,若a>0,b>0,则
≥
当且仅当a=b时取等号,这个不等式就叫做基本不等式.
在数学中,我们把 叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数;
定义基本不等式
文字语言:
两个正数的算术平均数不小于它们的几何平均数
从不同角度认识基本不等式
问题1:基本不等式 从数列的
角度,还可以怎么表述?
两个正数的等差中项不小于它们的等比中项
从不同角度认识基本不等式
A
B
C
E
a
b
O
D
几何意义:
证明:要证
只要证
①
要证②,只要证
②
要证③,只要证
③
显然, ④是成立的.当且仅当a=b时, ④中的等号成立.
分析法
思考:你还能给出基本不等式 的其他证明吗?
执果索因
证明基本不等式
④
问题3:你能否借助已证的重要不等式 ,分析基本不等式 的成立性呢?
证明基本不等式
解:如图设BC=x ,CD=y ,
则xy=100,
篱笆的长为2(x+y)m.
当且仅当 时,等号成立
因此,这个矩形的长、宽都为10m时,所用的篱笆最短,最短的篱笆是40m.
此时x=y=10.
x=y
A
B
D
C
例:(1)如图,用篱笆围成一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?
运用基本不等式求最值
因此,这个矩形的长、宽都为9m时,
菜园面积最大,最大面积是81m2
A
B
D
C
运用基本不等式求最值
例:(2)如图,用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?
知识方法小结
数学建模 数形结合
运用基本不等式求最值的条件:
一正、二定、三相等
布置作业
课堂作业:教材第100页习题A组第1,2题
课后作业:课后在网上查找基本不等式的其他代数几何证明方法,整理并相互交流。
思考:由基本不等式 出发,
你还能推导出哪些公式?
课后思考题
谢谢大家,敬请指导!
