高中数学人教新课标A版选修4-6第一讲 整数的整除1.整除的概念和性质 课件 20张PPT
文档属性
| 名称 | 高中数学人教新课标A版选修4-6第一讲 整数的整除1.整除的概念和性质 课件 20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 21:47:07 | ||
图片预览







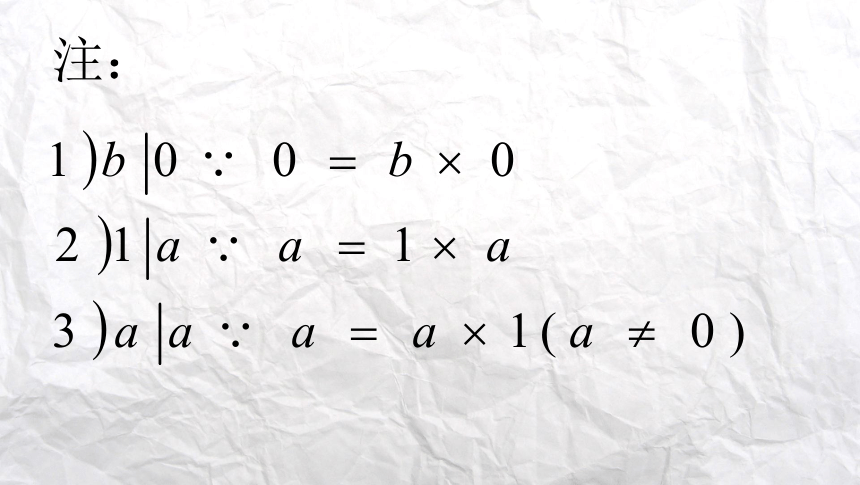

文档简介
(共20张PPT)
2
0
1
9
人教A版选修4-6《初等数论初步》
1.1整数的整除
1、 以前学习过的整数加法,减法,乘法运算得到的结果有什么特点?
整数的加法,减法,乘法运算得到的结果为整数。两个整数的商不一定是整数。
2、整数除法的商又是怎样的?
从以前学过的乘法中我们知道,若A×B=C,那么C÷B=A或C÷A=B
也就是说乘法和除法是互逆的运算。
例如:
3×2=6
6÷2=3
6÷3=2
若有六条鱼,平均一只猫可得几条鱼?
若是再多一条鱼,平均一只猫可得几条鱼呢?
6÷2=3
7不是2的倍数,7不能被2整除,说明7条鱼不能平均分给这两只猫
生活中这样的例子还有很多,我们从数学的角度该怎样理解,又该怎样定义呢?它们又有怎样的性质?这就是我们今天要一起研究的问题。
整数的整除
我们知道,乘法与除法是互逆的两种运算。要判断一个整数能否除尽另一个整数,只需考察被除数能否写成除数和某个整数的乘积。只有当被除数可以表示为除数和某个整数的乘积时,除数恰好能除尽被除数。此时,我们就说除数整除被除数,或者说被除数能被除数整除。
整除的定义:
一般地,设a,b为整数,且b≠0,如果存在整数q,使得a=bq,那么称b整除a,或者a能被b整除,记作b|a,并且称b是a的因数,a是b的倍数。如果这样的整数q不存在,就称b不能整除a。
例如:6|-24,-4|56,8|0
注:
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
解:
(1)因为a|b,b|a,所以存在整数m,n使得b=ma,a=nb,即b=ma=mnb,
又因为b≠0,所以mn=1,
即m=n=1或m=n=-1
所以a=b或a=-b
(2)因为a|b,b|c,所以存在整数m,n使得b=ma,c=nb,即c=nb=nma,
又m,n是整数,所以mn也是整数,即存在整数p,使得p=mn
所以c=pa
即a|c
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
解:
(3)因为a|b,a|c,所以存在整数m,n使得b=ma,c=na,那么bx+cy=xma+yna=(xm+yn)a,
又因为x,y,m,n,都是整数,所以存在整数q=xm+yn
即bx+cy=qa
所以a|bx+cy
如何判断一个非零整数整除给定的正整数?对某些特殊的非零整数,我们可以通过观察发现一些简单的判别方法。
例如:
(1)能被2整除的数:个位数字为0,2,4,6,8中的一个
(2)能被5整除的数:个位数字是0或5
(3)能被3整除的数:各个数位上的数字之和能被3整除
(4)能被9整除的数:各个数位上的数字之和能被9整除
例题分析:
1、一个正整数的各位数字之和能被3整除,那么这个正整数能被3整除
证明:设N为4位正整数,且它的个、十、百和千位数字依次为a,b,c,d
练习:
1.若五位数12a34是3的倍数,那么a是
探究:
2、一个正整数的各位数字之和能被9整除,那么这个正整数能被9整除。
3、一个正整数的奇数位数字之和与偶数位数字之和的差能被11整除,那么这个正整数能被11整除。
4、一个正整数的末三位数字组成的数与末三位数字之前的数字组成的数之差能被7(或11)整除,那么这个正整数能被7(或11)整除。
例1 判断710316能否被9,11整除
解:因为7+1+0+3+1+6=18能被9整除,
所以710316能被9整除
又因为710316的奇数位数字之和为6+3+1=10,偶数位数字之和为1+0+7=8,而10-8=2不能被11整除,所以710316不能被11整除
练习:
1、判断下列整数中哪些能分别被3,7,9,11整除:
45,98,120,189,1001,1331,56382
作业:
课本第7页:1,2
课时作业:第一课时
2
0
1
9
谢谢您的观看
2
0
1
9
人教A版选修4-6《初等数论初步》
1.1整数的整除
1、 以前学习过的整数加法,减法,乘法运算得到的结果有什么特点?
整数的加法,减法,乘法运算得到的结果为整数。两个整数的商不一定是整数。
2、整数除法的商又是怎样的?
从以前学过的乘法中我们知道,若A×B=C,那么C÷B=A或C÷A=B
也就是说乘法和除法是互逆的运算。
例如:
3×2=6
6÷2=3
6÷3=2
若有六条鱼,平均一只猫可得几条鱼?
若是再多一条鱼,平均一只猫可得几条鱼呢?
6÷2=3
7不是2的倍数,7不能被2整除,说明7条鱼不能平均分给这两只猫
生活中这样的例子还有很多,我们从数学的角度该怎样理解,又该怎样定义呢?它们又有怎样的性质?这就是我们今天要一起研究的问题。
整数的整除
我们知道,乘法与除法是互逆的两种运算。要判断一个整数能否除尽另一个整数,只需考察被除数能否写成除数和某个整数的乘积。只有当被除数可以表示为除数和某个整数的乘积时,除数恰好能除尽被除数。此时,我们就说除数整除被除数,或者说被除数能被除数整除。
整除的定义:
一般地,设a,b为整数,且b≠0,如果存在整数q,使得a=bq,那么称b整除a,或者a能被b整除,记作b|a,并且称b是a的因数,a是b的倍数。如果这样的整数q不存在,就称b不能整除a。
例如:6|-24,-4|56,8|0
注:
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
解:
(1)因为a|b,b|a,所以存在整数m,n使得b=ma,a=nb,即b=ma=mnb,
又因为b≠0,所以mn=1,
即m=n=1或m=n=-1
所以a=b或a=-b
(2)因为a|b,b|c,所以存在整数m,n使得b=ma,c=nb,即c=nb=nma,
又m,n是整数,所以mn也是整数,即存在整数p,使得p=mn
所以c=pa
即a|c
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
思考题:
由整除的概念,你能否推出下列整除的基本性质?
(1)若a|b,b|a,则a=b或a=-b
(2)若a|b,b|c,则a|c
(3)若a|b,a|c,则对任意整数x,y恒有a|bx+cy
解:
(3)因为a|b,a|c,所以存在整数m,n使得b=ma,c=na,那么bx+cy=xma+yna=(xm+yn)a,
又因为x,y,m,n,都是整数,所以存在整数q=xm+yn
即bx+cy=qa
所以a|bx+cy
如何判断一个非零整数整除给定的正整数?对某些特殊的非零整数,我们可以通过观察发现一些简单的判别方法。
例如:
(1)能被2整除的数:个位数字为0,2,4,6,8中的一个
(2)能被5整除的数:个位数字是0或5
(3)能被3整除的数:各个数位上的数字之和能被3整除
(4)能被9整除的数:各个数位上的数字之和能被9整除
例题分析:
1、一个正整数的各位数字之和能被3整除,那么这个正整数能被3整除
证明:设N为4位正整数,且它的个、十、百和千位数字依次为a,b,c,d
练习:
1.若五位数12a34是3的倍数,那么a是
探究:
2、一个正整数的各位数字之和能被9整除,那么这个正整数能被9整除。
3、一个正整数的奇数位数字之和与偶数位数字之和的差能被11整除,那么这个正整数能被11整除。
4、一个正整数的末三位数字组成的数与末三位数字之前的数字组成的数之差能被7(或11)整除,那么这个正整数能被7(或11)整除。
例1 判断710316能否被9,11整除
解:因为7+1+0+3+1+6=18能被9整除,
所以710316能被9整除
又因为710316的奇数位数字之和为6+3+1=10,偶数位数字之和为1+0+7=8,而10-8=2不能被11整除,所以710316不能被11整除
练习:
1、判断下列整数中哪些能分别被3,7,9,11整除:
45,98,120,189,1001,1331,56382
作业:
课本第7页:1,2
课时作业:第一课时
2
0
1
9
谢谢您的观看
