教版数学九年级下册28.2.2 应用举例(第3课时)方位角问题课件(共18张PPT)
文档属性
| 名称 | 教版数学九年级下册28.2.2 应用举例(第3课时)方位角问题课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 247.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 13:27:25 | ||
图片预览




文档简介
课件18张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第3课时)
方位角问题
1. 正确理解方位角的概念,能运用解直角三角形知识解决方位角的问题; (重点)
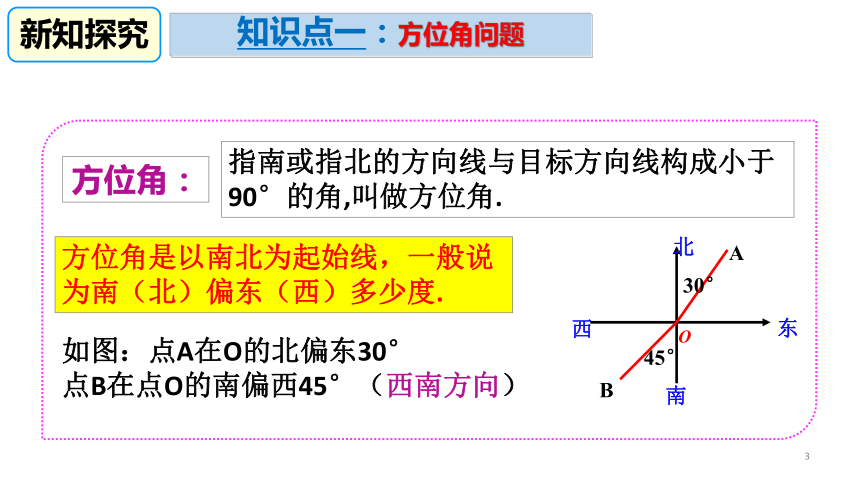
2. 能够掌握综合性较强的题型、融会贯通地运用相关的数学知识,进一步提高运用解直角三角形知识分析解决问题的综合能力. (重点、难点)学习目标3知识点一:方位角问题方位角:方位角是以南北为起始线,一般说为南(北)偏东(西)多少度.指南或指北的方向线与目标方向线构成小于90°的角,叫做方位角.如图:点A在O的北偏东30°
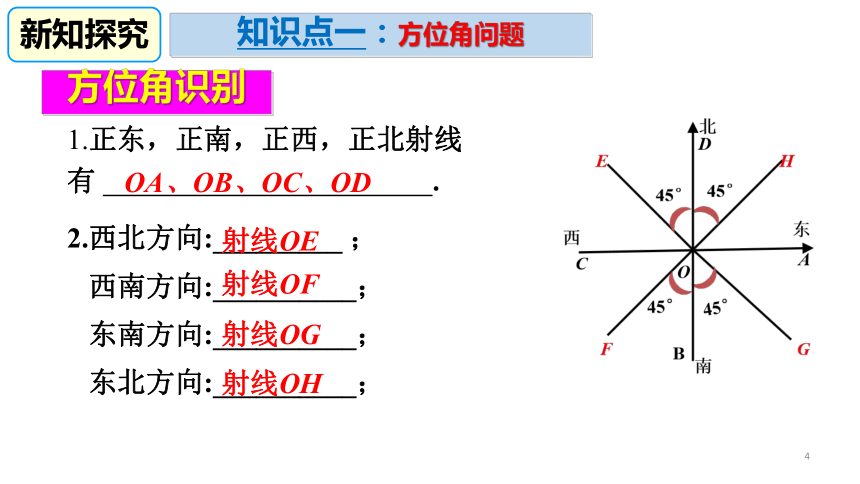
点B在点O的南偏西45°(西南方向)新知探究4方位角识别1.正东,正南,正西,正北射线有 .2.西北方向:_________ ;
西南方向:__________;
东南方向:__________;
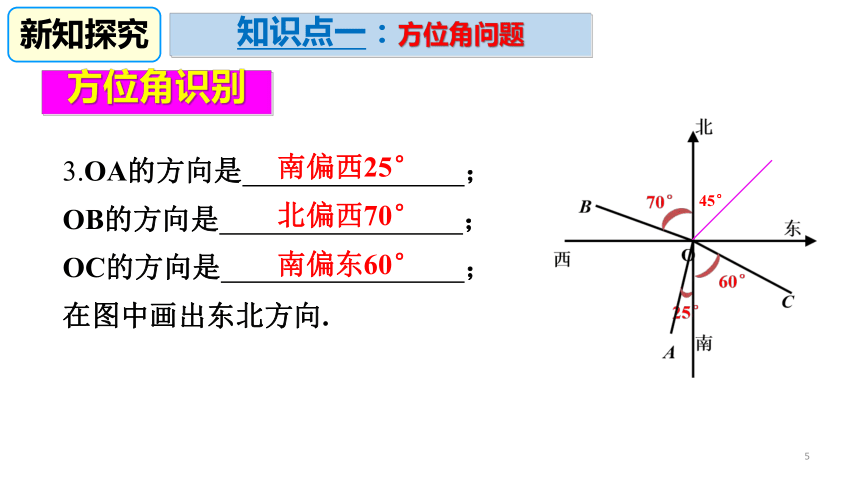
东北方向:__________; OA、OB、OC、OD射线OE射线OF射线OG射线OH知识点一:方位角问题新知探究5方位角识别3.OA的方向是 ;
OB的方向是 ;
OC的方向是 ;
在图中画出东北方向.南偏西25°北偏西70°南偏东60°45°知识点一:方位角问题新知探究6例1 如图, 一艘海轮位于灯塔P的 北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B 处.这时,B 处距离灯塔 P有多远(结果取整数)?cos 25°≈0.9063,sin34°≈0.5577.知识点二:方位角问题的实际应用典例精析7cos 25°≈0.9063,sin34°≈0.5577解:如图,在Rt△APC中,
PC =PA ? cos(90°-65°)
=80 × cos 25°≈72. 505. 在 Rt△BPC 中, ∠B = 34°,因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约 130 n mile.知识点二:方位角问题的实际应用典例精析8 小明在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为 米.知识点二:方位角问题的实际应用巩固训练9 利用解直角三角形解决方位角的问题时,“同方向的方向线互相平行”是其中的一个隐含条件.知识点二:方位角问题的实际应用归纳总结101.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的A处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB是( )
A.2海里
B.2sin 55°海里
C.2cos 55°海里
D.2tan 55°海里C知识点二:方位角问题的实际应用学以致用112.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
A.15 海里
B.30海里
C.45海里
D.30 海里B知识点二:方位角问题的实际应用学以致用123.如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,
测得点A在点C的北偏西60°
方向上,则点A到河岸BC的距
离为________.知识点二:方位角问题的实际应用学以致用D134.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?知识点二:方位角问题的实际应用学以致用14解:由点A作BD的垂线交BD的延长线于点F,垂足为F,∠AFD=90°由题意图示可知∠ABD=30°∠ADB=90°+30°=120°
∴∠BAD=∠ABD=30°
∴AD=BD=12在Rt△ADF中,∠ADF=60°∴∵10.4 > 8∴没有触礁危险知识点二:方位角问题的实际应用学以致用∴∴AF≈ 10.4(n mile)15利用解直角三角形解决实际问题的一般过程课堂小结161.如图,在距离铁轨200米的B处,观察由满洲里开往北京的“和谐号”列车,当火车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,火车车头到达C处,恰好位于B处的西北方向上,则这时段火车的平均速度是( )米/秒
A.20( +1)
B.20( -1)
C.200
D.300A家庭作业2. 如图,海上B、C两岛分别位于A岛的正东和正北方
向,一艘船从A岛出发,以18海里/时的速度向正北
方向航行2小时到达C岛,此时测得B岛在C岛的南
偏东43°方向,则A、B两岛之间的距离为 .
(结果精确到0.1海里,参考数据:sin43°=0.68,
cos43°=0.73,tan43°=0.93)
家庭作业18 3.如图“华庆号”船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且∠CBA=30°,∠CAB=60°.
(1)求此时船A与海岛B之间的距离.
(2)若海岛B周围16海里内有海礁,
“华庆号”船继续沿AC向C航行有无
触礁危险?请说明理由.家庭作业
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第3课时)
方位角问题
1. 正确理解方位角的概念,能运用解直角三角形知识解决方位角的问题; (重点)
2. 能够掌握综合性较强的题型、融会贯通地运用相关的数学知识,进一步提高运用解直角三角形知识分析解决问题的综合能力. (重点、难点)学习目标3知识点一:方位角问题方位角:方位角是以南北为起始线,一般说为南(北)偏东(西)多少度.指南或指北的方向线与目标方向线构成小于90°的角,叫做方位角.如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)新知探究4方位角识别1.正东,正南,正西,正北射线有 .2.西北方向:_________ ;
西南方向:__________;
东南方向:__________;
东北方向:__________; OA、OB、OC、OD射线OE射线OF射线OG射线OH知识点一:方位角问题新知探究5方位角识别3.OA的方向是 ;
OB的方向是 ;
OC的方向是 ;
在图中画出东北方向.南偏西25°北偏西70°南偏东60°45°知识点一:方位角问题新知探究6例1 如图, 一艘海轮位于灯塔P的 北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B 处.这时,B 处距离灯塔 P有多远(结果取整数)?cos 25°≈0.9063,sin34°≈0.5577.知识点二:方位角问题的实际应用典例精析7cos 25°≈0.9063,sin34°≈0.5577解:如图,在Rt△APC中,
PC =PA ? cos(90°-65°)
=80 × cos 25°≈72. 505. 在 Rt△BPC 中, ∠B = 34°,因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约 130 n mile.知识点二:方位角问题的实际应用典例精析8 小明在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为 米.知识点二:方位角问题的实际应用巩固训练9 利用解直角三角形解决方位角的问题时,“同方向的方向线互相平行”是其中的一个隐含条件.知识点二:方位角问题的实际应用归纳总结101.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的A处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB是( )
A.2海里
B.2sin 55°海里
C.2cos 55°海里
D.2tan 55°海里C知识点二:方位角问题的实际应用学以致用112.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
A.15 海里
B.30海里
C.45海里
D.30 海里B知识点二:方位角问题的实际应用学以致用123.如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,
测得点A在点C的北偏西60°
方向上,则点A到河岸BC的距
离为________.知识点二:方位角问题的实际应用学以致用D134.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?知识点二:方位角问题的实际应用学以致用14解:由点A作BD的垂线交BD的延长线于点F,垂足为F,∠AFD=90°由题意图示可知∠ABD=30°∠ADB=90°+30°=120°
∴∠BAD=∠ABD=30°
∴AD=BD=12在Rt△ADF中,∠ADF=60°∴∵10.4 > 8∴没有触礁危险知识点二:方位角问题的实际应用学以致用∴∴AF≈ 10.4(n mile)15利用解直角三角形解决实际问题的一般过程课堂小结161.如图,在距离铁轨200米的B处,观察由满洲里开往北京的“和谐号”列车,当火车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,火车车头到达C处,恰好位于B处的西北方向上,则这时段火车的平均速度是( )米/秒
A.20( +1)
B.20( -1)
C.200
D.300A家庭作业2. 如图,海上B、C两岛分别位于A岛的正东和正北方
向,一艘船从A岛出发,以18海里/时的速度向正北
方向航行2小时到达C岛,此时测得B岛在C岛的南
偏东43°方向,则A、B两岛之间的距离为 .
(结果精确到0.1海里,参考数据:sin43°=0.68,
cos43°=0.73,tan43°=0.93)
家庭作业18 3.如图“华庆号”船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且∠CBA=30°,∠CAB=60°.
(1)求此时船A与海岛B之间的距离.
(2)若海岛B周围16海里内有海礁,
“华庆号”船继续沿AC向C航行有无
触礁危险?请说明理由.家庭作业
