28.2 解直角三角形及其应用-应用举例复习课课件(20张ppt)
文档属性
| 名称 | 28.2 解直角三角形及其应用-应用举例复习课课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 423.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 13:29:45 | ||
图片预览




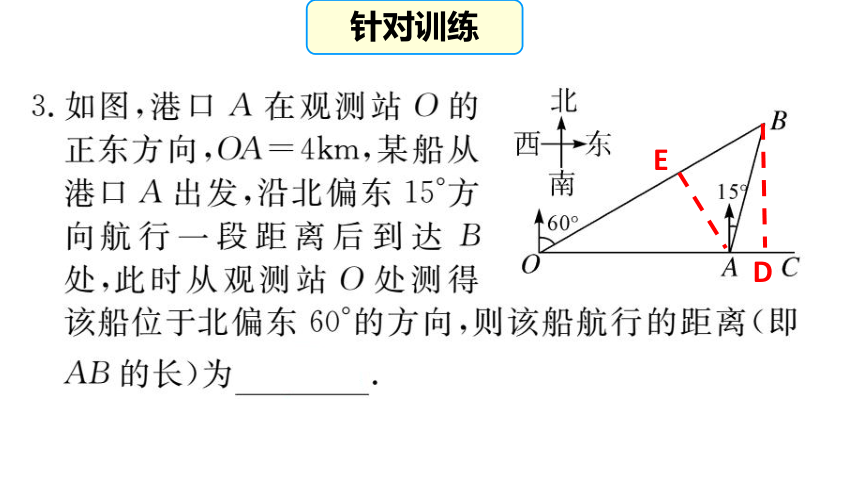
文档简介
课件20张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第4课时)
复习课
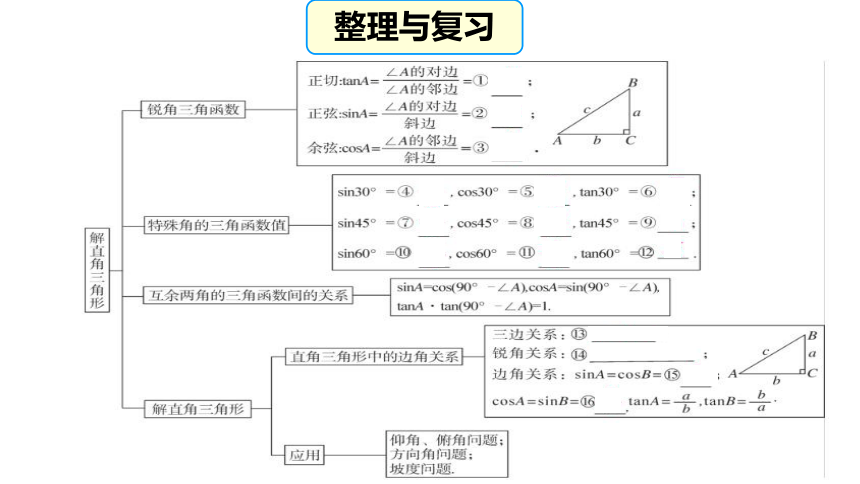
学习目标1. 掌握解直角三角形的概念和直角三角形中的五个元素之间的联系。
2. 熟练掌握解直角三角形的方法;并能运用解直角三角形的知识解决仰角俯角、坡角、方位角等问题;
3.能够掌握综合性较强的题型,融会贯通地运用解直角三角形的知识灵活解决问题。 整理与复习直角三角形可解的条件:
解直角三角形时,除直角外,再知道其中的2个元素(至少有一个是边), 就可以求出其余的3个未知元素.解直角三角形的方法:
①一边一锐角:
先由两锐角互余关系求出另一锐角;
知斜边,用正弦(或余弦)求另两边;
知直角边,用正切求另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.整理与复习1.如图,Rt△ABC中,∠C=90°,(2)若∠A=30°,BC=3,则AC=(1)若∠B=60°,AB=6,则AC=(3)若∠A=α°,AC=3,则BC=(4)若∠A=α°,BC=m,则AC=温故知新一、“背靠背”型
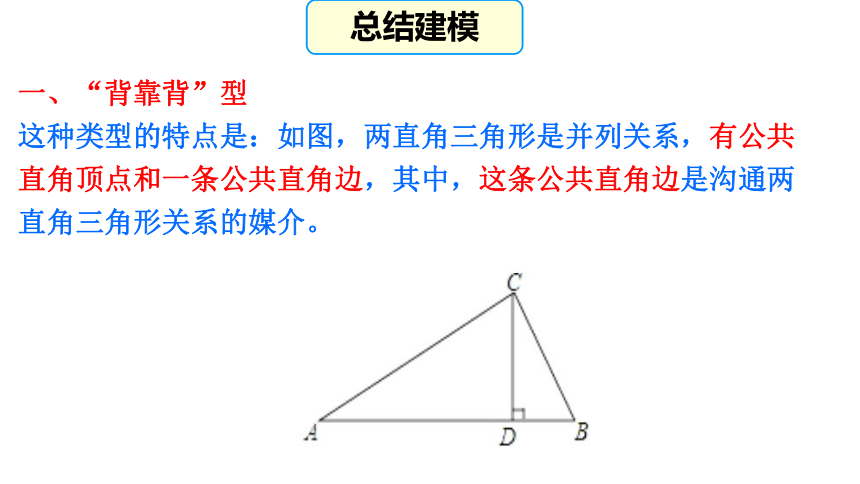
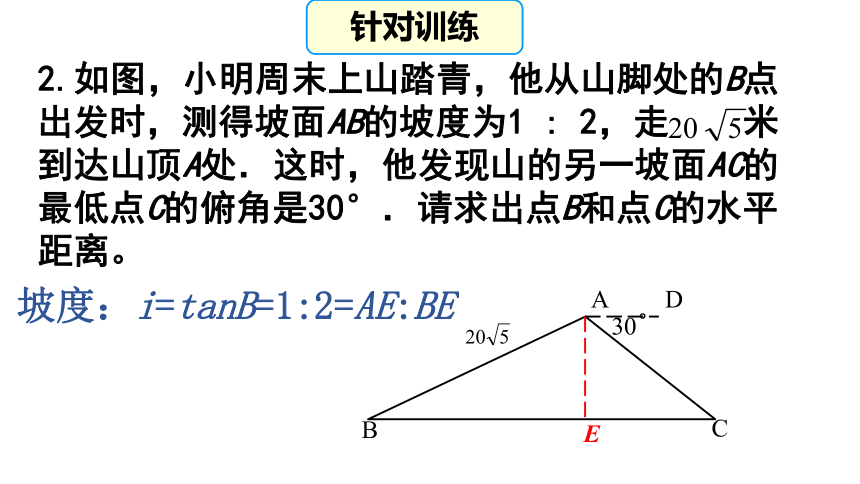
这种类型的特点是:如图,两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。总结建模AD°CBE30针对训练2.如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离。
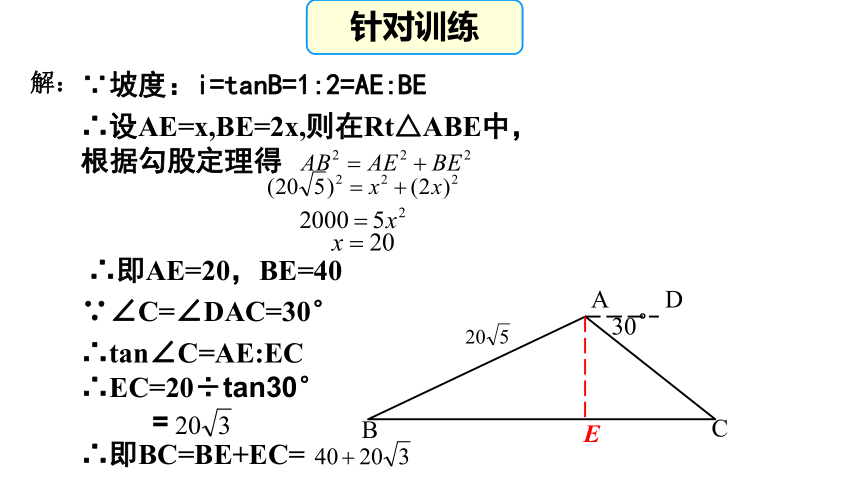
坡度:i=tanB=1:2=AE:BEAD°CBE30针对训练∵坡度:i=tanB=1:2=AE:BE解:
∴设AE=x,BE=2x,则在Rt△ABE中,
根据勾股定理得∴即AE=20,BE=40∵∠C=∠DAC=30°∴tan∠C=AE:EC
∴EC=20÷tan30°
=∴即BC=BE+EC=DE针对训练二、“母抱子”型
这种类型的特点是,一个直角三角形包含在另一个直角三角形中,两直角三角形有公共直角和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。总结建模针对训练D三、“拥抱”型
这种类型的特点是:两直角三角形以交叉方式出现。
总结建模5. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)针对训练甲45km/h→↑乙36km/h45°58°解:设B处距离码头O x km,
在Rt△CAO中,∠CAO=45°,
∴△CAO是等腰直角三角形
∴CO=AO=AB+BO=45×0.1+x=4.5+x
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=DO:BO ,
∴DO=BO · tan∠DBO=x · tan58°,
∵DC+CO=x · tan58°,
∴36×0.1+(4.5+x)=x · tan58°,
8.1+x≈1.6x
x ≈ 13.5
因此,B处距离码头O大约13.5km.45°58°解直角三角形的方法:
角的关系有互余,边的关系有勾股;有斜边用正余弦,
没有斜边用正切;选用乘法毋用除,采取原始避中间。
(既可以由已知数据又可由中间数据求解时,则用已知数据,尽量避免用中间数据。)总结归纳总结归纳一、“背靠背”型 二、“母抱子”型 三、“拥抱”型ABEDC1.数形结合思想.2.方程思想.3.转化(化归)思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想:1.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).2.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 (根号保留). 家庭作业3. 如图,防洪大堤的横截面是梯形 ABCD,其中AD//BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号) 4.如图,在数学活动课中,小敏为了测量旗杆AB 的高度,站在教学楼上的C 处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD 为9 m,则旗杆的高度是多少?(结果保留根号)
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第4课时)
复习课
学习目标1. 掌握解直角三角形的概念和直角三角形中的五个元素之间的联系。
2. 熟练掌握解直角三角形的方法;并能运用解直角三角形的知识解决仰角俯角、坡角、方位角等问题;
3.能够掌握综合性较强的题型,融会贯通地运用解直角三角形的知识灵活解决问题。 整理与复习直角三角形可解的条件:
解直角三角形时,除直角外,再知道其中的2个元素(至少有一个是边), 就可以求出其余的3个未知元素.解直角三角形的方法:
①一边一锐角:
先由两锐角互余关系求出另一锐角;
知斜边,用正弦(或余弦)求另两边;
知直角边,用正切求另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.整理与复习1.如图,Rt△ABC中,∠C=90°,(2)若∠A=30°,BC=3,则AC=(1)若∠B=60°,AB=6,则AC=(3)若∠A=α°,AC=3,则BC=(4)若∠A=α°,BC=m,则AC=温故知新一、“背靠背”型
这种类型的特点是:如图,两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。总结建模AD°CBE30针对训练2.如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离。
坡度:i=tanB=1:2=AE:BEAD°CBE30针对训练∵坡度:i=tanB=1:2=AE:BE解:
∴设AE=x,BE=2x,则在Rt△ABE中,
根据勾股定理得∴即AE=20,BE=40∵∠C=∠DAC=30°∴tan∠C=AE:EC
∴EC=20÷tan30°
=∴即BC=BE+EC=DE针对训练二、“母抱子”型
这种类型的特点是,一个直角三角形包含在另一个直角三角形中,两直角三角形有公共直角和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。总结建模针对训练D三、“拥抱”型
这种类型的特点是:两直角三角形以交叉方式出现。
总结建模5. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)针对训练甲45km/h→↑乙36km/h45°58°解:设B处距离码头O x km,
在Rt△CAO中,∠CAO=45°,
∴△CAO是等腰直角三角形
∴CO=AO=AB+BO=45×0.1+x=4.5+x
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=DO:BO ,
∴DO=BO · tan∠DBO=x · tan58°,
∵DC+CO=x · tan58°,
∴36×0.1+(4.5+x)=x · tan58°,
8.1+x≈1.6x
x ≈ 13.5
因此,B处距离码头O大约13.5km.45°58°解直角三角形的方法:
角的关系有互余,边的关系有勾股;有斜边用正余弦,
没有斜边用正切;选用乘法毋用除,采取原始避中间。
(既可以由已知数据又可由中间数据求解时,则用已知数据,尽量避免用中间数据。)总结归纳总结归纳一、“背靠背”型 二、“母抱子”型 三、“拥抱”型ABEDC1.数形结合思想.2.方程思想.3.转化(化归)思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想:1.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).2.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 (根号保留). 家庭作业3. 如图,防洪大堤的横截面是梯形 ABCD,其中AD//BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号) 4.如图,在数学活动课中,小敏为了测量旗杆AB 的高度,站在教学楼上的C 处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD 为9 m,则旗杆的高度是多少?(结果保留根号)
