2019-2020学年北师大版九下数学第三章圆单元测试卷(含答案)
文档属性
| 名称 | 2019-2020学年北师大版九下数学第三章圆单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 13:43:28 | ||
图片预览

文档简介
2020春北师大版九下数学第三章圆单元测试卷
(总分:100分 时间:120分钟)
一、选择题(每题3分,共30分)
1.如图1所示,是直径,点是中点,弦且平分,连,度数为( )
A. B. C. D.
图1 图2 图3
2.下列命题中,真命题是( )
A.圆周角等于圆心角的一半 B.等弧所对的圆周角相等
C.垂直于半径的直线是圆的切线 D.过弦的中点的直线必经过圆心
3.半径分别为和的两个圆的圆心距为,若,则这两个圆的位置关系一定是( )
A.相交 B.相切 C.内切或相交 D.外切或相交
4.过⊙内一点的最长弦长为,最短弦长为,那么长为( )
A. B. C. D.
5.半径相等的圆的内接正三角形,正方形边长之比为( )
A. B.: C. D.
6.如图2,已知⊙的直径与弦的夹角为,过点的切线与的延长线交于点,则等于( )
A. B. C. D.
7.如图3所示,在直角坐标系中,点坐标为,⊙的半径为,为轴上一动点,切⊙于点,则当最小时,点的坐标为( )
A. B. C.或 D.
在半径为的圆中,的圆心角所对的弧长是( )
A. B. C. D.
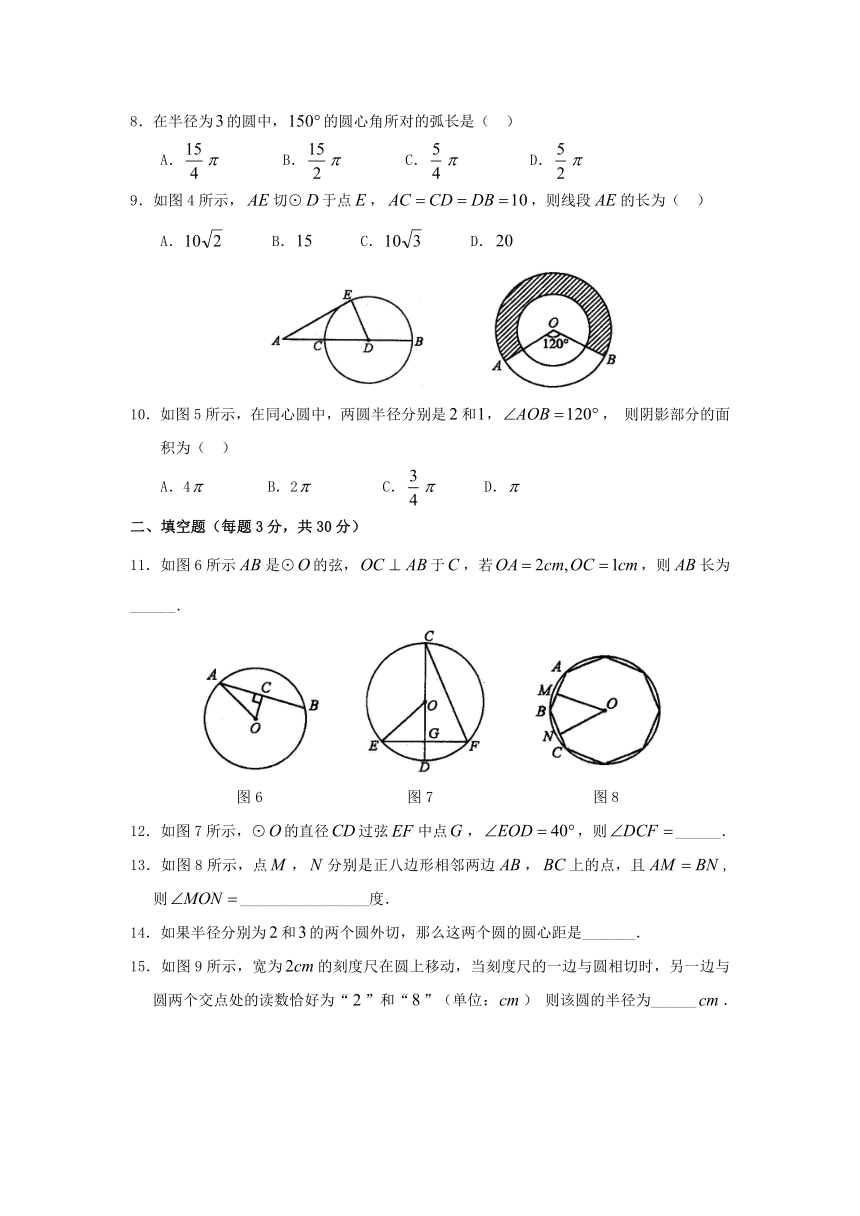
9.如图4所示,切⊙于点,,则线段的长为( )
A. B. C. D.
10.如图5所示,在同心圆中,两圆半径分别是和,,则阴影部分的面积为( )
A.4 B.2 C. D.
二、填空题(每题3分,共30分)
11.如图6所示是⊙的弦,于,若,则长为______.
图6 图7 图8
12.如图7所示,⊙的直径过弦中点,,则______.
13.如图8所示,点,分别是正八边形相邻两边,上的点,且,则_________________度.
14.如果半径分别为和的两个圆外切,那么这两个圆的圆心距是_______.
15.如图9所示,宽为的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“”和“”(单位:)则该圆的半径为______.
图9 图10 图11
16.如图10所示,⊙的圆心坐标为,若⊙的半径为,则直线与⊙的位置关系是________.
17.如图11所示,是△的内心,,则______.
18.圆锥底面圆的半径为,母线长为,则它的侧面积为________.(用含的式子表示)
19.已知圆锥的底面半径为,母线长为,则它的侧面展开图的圆心角为_______.
20.矩形中,,如果分别以,为圆心的两圆相切,点在⊙内,点在⊙外,那么⊙的半径的取值范围为________.
三、解答题(共40分)
21.(6分)如图所示,是⊙的直径,弦于,若,求⊙半径的长.
22.(6分)如图所示,是⊙的直径,切⊙于,交⊙于,是边上的中点,连结,与⊙相切吗?若相切,请加以证明,若不相切,请说明理由.
23.(10分)已知:如图所示,直线交⊙于,两点,的垂线切⊙于点,过点作⊙的直径.
(1)求证:平分;(2)若,求⊙的直径.
24.(10分)“五一”节,小雯和同学一起到游乐场玩大型摩天轮,摩天轮的半径为,匀速转动一周需要,小雯所坐最底部的车厢(离地面).
(1)经过后小雯到达点如图所示,此时他离地面的高度是多少.
(2)在摩天轮滚动的过程中,小雯将有多长时间连续保持在离地面不低于的空中.
25.(8分)如图所示,⊙半径为,弦,为弧的中点,为弦的中点,且在上,求四边形的面积.
参考答案
1.C 2.B 3.D 4.A 5.B 6.B 7.D 8.D 9.C 10.B
11.2cm 12.20° 13.45 14.5 15. 16.相交
17.20° 18.40cm2 19.160° 20.121.解:连接OA,∵CE是直径,AB⊥CE,∴AD=AB=3.
∵CD=2,∴OD=OC-CD=OA-2.由勾股定理,得OA2-OD2=AD2,
∴OA2-(OA-2)2=92,解得OA=,∴⊙O的半径等于.
22.解:相切,证OP⊥PE即可.
23.解:(1)连BE,BC,∠CAB+∠ABC=90°,∠DCA=∠ABC,
∴∠DAC,∠CAB,AC平分∠DAB.
(2)DA=2,AC=4,∠ACD=30°,∠ABC=∠DCA=30°,∵AC=4,∴AB=8.
24.(1)10.5 (2)×12=4(min).
25.解:连结OA交BD于点F,连接OB.∵OA在直径上且点A是BD中点,
∴OA⊥BD,BF=DF=.
在Rt△BOF中,由勾股定理得OF2=OB2-BF2,
OF= =.
∵点E是AC中点,∴AE=CE.又∵△ADE和△CDE同高,∴S△CDE=S△ADE,
同理S△CBE =S△ABE,∴S△BCD =S△CDE +S△CBE =S△ADE +S△ABE =S△ABD =,
∴S四边形ABCD=S△ABD +S△BCD =2.
(总分:100分 时间:120分钟)
一、选择题(每题3分,共30分)
1.如图1所示,是直径,点是中点,弦且平分,连,度数为( )
A. B. C. D.
图1 图2 图3
2.下列命题中,真命题是( )
A.圆周角等于圆心角的一半 B.等弧所对的圆周角相等
C.垂直于半径的直线是圆的切线 D.过弦的中点的直线必经过圆心
3.半径分别为和的两个圆的圆心距为,若,则这两个圆的位置关系一定是( )
A.相交 B.相切 C.内切或相交 D.外切或相交
4.过⊙内一点的最长弦长为,最短弦长为,那么长为( )
A. B. C. D.
5.半径相等的圆的内接正三角形,正方形边长之比为( )
A. B.: C. D.
6.如图2,已知⊙的直径与弦的夹角为,过点的切线与的延长线交于点,则等于( )
A. B. C. D.
7.如图3所示,在直角坐标系中,点坐标为,⊙的半径为,为轴上一动点,切⊙于点,则当最小时,点的坐标为( )
A. B. C.或 D.
在半径为的圆中,的圆心角所对的弧长是( )
A. B. C. D.
9.如图4所示,切⊙于点,,则线段的长为( )
A. B. C. D.
10.如图5所示,在同心圆中,两圆半径分别是和,,则阴影部分的面积为( )
A.4 B.2 C. D.
二、填空题(每题3分,共30分)
11.如图6所示是⊙的弦,于,若,则长为______.
图6 图7 图8
12.如图7所示,⊙的直径过弦中点,,则______.
13.如图8所示,点,分别是正八边形相邻两边,上的点,且,则_________________度.
14.如果半径分别为和的两个圆外切,那么这两个圆的圆心距是_______.
15.如图9所示,宽为的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“”和“”(单位:)则该圆的半径为______.
图9 图10 图11
16.如图10所示,⊙的圆心坐标为,若⊙的半径为,则直线与⊙的位置关系是________.
17.如图11所示,是△的内心,,则______.
18.圆锥底面圆的半径为,母线长为,则它的侧面积为________.(用含的式子表示)
19.已知圆锥的底面半径为,母线长为,则它的侧面展开图的圆心角为_______.
20.矩形中,,如果分别以,为圆心的两圆相切,点在⊙内,点在⊙外,那么⊙的半径的取值范围为________.
三、解答题(共40分)
21.(6分)如图所示,是⊙的直径,弦于,若,求⊙半径的长.
22.(6分)如图所示,是⊙的直径,切⊙于,交⊙于,是边上的中点,连结,与⊙相切吗?若相切,请加以证明,若不相切,请说明理由.
23.(10分)已知:如图所示,直线交⊙于,两点,的垂线切⊙于点,过点作⊙的直径.
(1)求证:平分;(2)若,求⊙的直径.
24.(10分)“五一”节,小雯和同学一起到游乐场玩大型摩天轮,摩天轮的半径为,匀速转动一周需要,小雯所坐最底部的车厢(离地面).
(1)经过后小雯到达点如图所示,此时他离地面的高度是多少.
(2)在摩天轮滚动的过程中,小雯将有多长时间连续保持在离地面不低于的空中.
25.(8分)如图所示,⊙半径为,弦,为弧的中点,为弦的中点,且在上,求四边形的面积.
参考答案
1.C 2.B 3.D 4.A 5.B 6.B 7.D 8.D 9.C 10.B
11.2cm 12.20° 13.45 14.5 15. 16.相交
17.20° 18.40cm2 19.160° 20.1
∵CD=2,∴OD=OC-CD=OA-2.由勾股定理,得OA2-OD2=AD2,
∴OA2-(OA-2)2=92,解得OA=,∴⊙O的半径等于.
22.解:相切,证OP⊥PE即可.
23.解:(1)连BE,BC,∠CAB+∠ABC=90°,∠DCA=∠ABC,
∴∠DAC,∠CAB,AC平分∠DAB.
(2)DA=2,AC=4,∠ACD=30°,∠ABC=∠DCA=30°,∵AC=4,∴AB=8.
24.(1)10.5 (2)×12=4(min).
25.解:连结OA交BD于点F,连接OB.∵OA在直径上且点A是BD中点,
∴OA⊥BD,BF=DF=.
在Rt△BOF中,由勾股定理得OF2=OB2-BF2,
OF= =.
∵点E是AC中点,∴AE=CE.又∵△ADE和△CDE同高,∴S△CDE=S△ADE,
同理S△CBE =S△ABE,∴S△BCD =S△CDE +S△CBE =S△ADE +S△ABE =S△ABD =,
∴S四边形ABCD=S△ABD +S△BCD =2.
