第2届信息学分区联赛普及组初赛试题
文档属性
| 名称 | 第2届信息学分区联赛普及组初赛试题 | 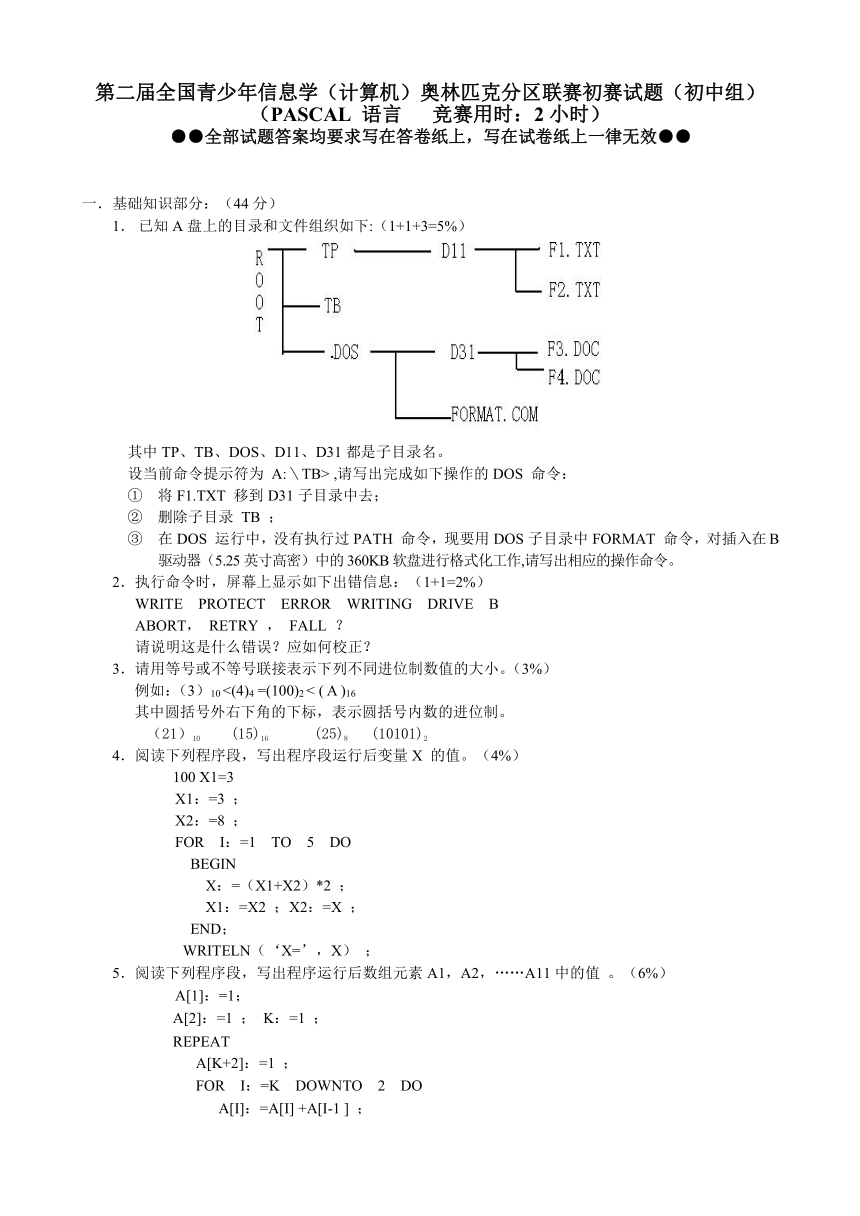 | |
| 格式 | zip | ||
| 文件大小 | 23.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2009-09-16 19:50:00 | ||
图片预览


文档简介
第二届全国青少年信息学(计算机)奥林匹克分区联赛初赛试题(初中组)
(PASCAL 语言 竞赛用时:2小时)
●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●
基础知识部分:(44分)
已知A盘上的目录和文件组织如下:(1+1+3=5%)
其中TP、TB、DOS、D11、D31都是子目录名。
设当前命令提示符为 A:\TB> ,请写出完成如下操作的DOS 命令:
① 将F1.TXT 移到D31子目录中去;
② 删除子目录 TB ;
③ 在DOS 运行中,没有执行过PATH 命令,现要用DOS子目录中FORMAT 命令,对插入在B驱动器(5.25英寸高密)中的360KB软盘进行格式化工作,请写出相应的操作命令。
2.执行命令时,屏幕上显示如下出错信息:(1+1=2%)
WRITE PROTECT ERROR WRITING DRIVE B
ABORT, RETRY , FALL ?
请说明这是什么错误?应如何校正?
3.请用等号或不等号联接表示下列不同进位制数值的大小。(3%)
例如:(3)10 <(4)4 =(100)2 < ( A )16
其中圆括号外右下角的下标,表示圆括号内数的进位制。
(21)10 (15)16 (25)8 (10101)2
4.阅读下列程序段,写出程序段运行后变量X 的值。(4%)
100 X1=3
X1:=3 ;
X2:=8 ;
FOR I:=1 TO 5 DO
BEGIN
X:=(X1+X2)*2 ;
X1:=X2 ;X2:=X ;
END;
WRITELN(‘X=’,X) ;
5.阅读下列程序段,写出程序运行后数组元素A1,A2,……A11中的值 。(6%)
A[1]:=1;
A[2]:=1 ; K:=1 ;
REPEAT
A[K+2]:=1 ;
FOR I:=K DOWNTO 2 DO
A[I]:=A[I] +A[I-1 ] ;
K:=K+1 ;
UNTIL K>=10 ;
6.已知:ACK(M,N)函数的计算公式如下: (4%)
N+1 M=0
ACK(M,N)= ACK(M-1,1) N=0
ACK(M-1,ACK(M,N-1) M≠0 且N≠0
请计算:ACK(1,2)与ACK(2,2)的值。
7.请写出对应计算如下算式的程序段:(4%)
Y=ANXN+AN-1XN-1+……A1X+A0
8.有N×N个数据组成如下方阵:(7%)
A11 A12 A13 …… A1N
A21 A22 A23 …… A2N
A31 A32 A33 …… A3N
…………
AN1 AN2 AN3 …… ANN
并已知: Aij = Aji
现将A11 ,A21,A22 ,A31 ,A32 ,A33 …存储在一维数组A[1],A[2],…A[(N*(N+1))/2] 中。
试问:任给i,j怎样求出K来,使得A[K]的值正好是Aij,请写出由i,j计算K值的表达式。
9.已知:A1,A2,……,A81 共有81个数,其中只有一个数比其它数大,要用最少的比较运算次数,把这个值大的数找出来(假设两个数比较一次能决定出大于、小于或等于这三种情况)请将以下算法补充完整:(9%)
第一步: S1 = A1 + A2 + …… + A27
S2 = A28 + A29 +……+ A54
第一次比较(S1,S2) :
S1 > S2 取 K=0
S1 < S2 取 K=27
S1 = S2 取 K=54
第二步: S1 = AK+1 + AK+2 + …… + AK+9
S2 = AK+10 + AK+11 +……+ AK+18
第二次比较(S1,S2) :
S1 > S2 取 K=
S1 < S2 取 K=
S1 = S2 取 K=
第三步: S1 = AK+1 + AK+2 + AK+3
S2 = AK+4 + AK+5 + AK+6
第三次比较(S1,S2) :
S1 > S2 取 K=
S1 < S2 取 K=
S1 = S2 取 K=
第四步: S1 = AK+1
S2 = AK+2
第四次比较(S1,S2) :
S1 > S2 为最大数
S1 < S2 为最大数,
S1 = S2 为最大数。
二.根据题目要求,补充完善以下程序:(56%)
1.[题 目] 15分(每空5分)
设有N个不同整数的数列:例如N=4时,有4个不同整数的数列为17,4,16,5。数列中的第1个数17,比它后面的三个数都大,则称数17的逆数为3。数列中的第2个数4比它后面的数都小,则称数4的逆数为0。同时记数列中全部逆数的和称为数列的逆数。上例中,数列17,4,16,5的逆数:为3+0+1+0=4。
[程序要求]:当给出N个不同整数的数列后,求出此数列的逆数。
[算法描述]:为求得上面问题的解,设置数组A:array[1..N] of Integer 和逆数计数器5,然后用一个二重循环求出数列的逆数。
[程 序]:
Const N=10;
Var i,j,s:integer;
A:array[1..N] of integer;
Begin
S:=0;
For I:=1 to n do read(a[I]);
For I:=1 to 1 do
For j:= 2 to n do
If a[I]>a[j] then 3 ;
Writeln('s=',s)
End.
2.[题 目] 20分(每空4分)
装球:设有n个盒子(n足够大,可装入任何数量的球),分别编号1,2,……。同时有k个小球(k>0),今将k 个小球装入到盒子中去。
装入规则如下:
第一个盒子不能为空。
装入必须严格按递增顺序进行。
例如,当k=8,n=6时,装入方法有1,2,5或1,3,4
在满足上面的两个条件下,要求有球的盒子尽可能多。
装完后,相邻盒子中球个数差的绝对值之和最小(未装的盒子不计)。
如上例中:
装入法1,2,5,则差的绝对值之和为2-1+5-2=4
装入法1,3,4,则差的绝对值之和为3-1+4-3=3
[程序要求]:给出k(k表示小球的个数)之后,求出满足上述四个条件的装入方法。
[算法描述]:设计一个数组A用数组元素代表盒子,然后依次装入小球。
[程序清单]
Const n=20;
Var i,j,k,l:integer;
A:array[1..n] of integer;
Begin
Readln(k);
1 ;
j:=1;
while 2 do begin
a[j]:=j; 3 ; j:=j+1
end;
l:=j-1;
while k>0 do begin
4 ;
k:=k-1;
l:=l-1;
end;
for I:=1 to 5 do
write(a[I]:4)
end.
3.[题 目] 21分(3+4+3+3+4+4)
积木游戏:设有n 个小木块排成一排,如下图:
……
游戏开始时,每个小木块向下的一面涂有红、黄、蓝三种颜色之中的一种(约定:0表示红色,1表示黄色,2表示兰色)。要求通过翻看与交换方式对小木块重新排列(翻看的规则为每个小木快只能看一次),最终成为下面的形状:
…… …… ……
红 蓝 黄
即相同颜色的木块排列在一起,设计一个翻看与交换的方案,使得用最少的交换次数实现上面的要求。
[算法描述]:翻看小木块时,可以从两端进行。
例如,设中间状态如下:
…… A …… B …… C ……
红 未翻过 蓝 黄
此时,可以从两个方向看,即从A或B处开始:
若看A则有三种可能性:
为红色,则不用交换
为兰色,交换一次,即A与B交换
为黄色,交换两次,即C与B交换一次,然后A与C再交换一次
此时,平均交换次数为1。
若看B,也有三种可能性:
为兰色,则不用交换
为红色,交换一次,即B与A交换。
为黄色,交换一次,即B与C交换。
此时,平均交换次数为2/3。
由此可见,从B处翻看直到游戏结束,次数最少符合题目要求。
[程 序]
Const n=20;
Var i,tem,r,b,y:integer;
a:array[1..n] of 0..2;
Begin
For i:=1 to n do read(a[i]);
r:=1; 1 ; y:=n;
while 2 do
if 3 then begin
tem:=a[r];a[r]:=a[b];a[b]:=tem;
r:=r+1
end
else if 4 then begin
tem:=a[b];a[b]:=a[y];a[y]:=tem;
5 ; 6 ;
end
else b:=b=1
for I:=1 to n do write(a[I]:3)
end.
(PASCAL 语言 竞赛用时:2小时)
●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●
基础知识部分:(44分)
已知A盘上的目录和文件组织如下:(1+1+3=5%)
其中TP、TB、DOS、D11、D31都是子目录名。
设当前命令提示符为 A:\TB> ,请写出完成如下操作的DOS 命令:
① 将F1.TXT 移到D31子目录中去;
② 删除子目录 TB ;
③ 在DOS 运行中,没有执行过PATH 命令,现要用DOS子目录中FORMAT 命令,对插入在B驱动器(5.25英寸高密)中的360KB软盘进行格式化工作,请写出相应的操作命令。
2.执行命令时,屏幕上显示如下出错信息:(1+1=2%)
WRITE PROTECT ERROR WRITING DRIVE B
ABORT, RETRY , FALL ?
请说明这是什么错误?应如何校正?
3.请用等号或不等号联接表示下列不同进位制数值的大小。(3%)
例如:(3)10 <(4)4 =(100)2 < ( A )16
其中圆括号外右下角的下标,表示圆括号内数的进位制。
(21)10 (15)16 (25)8 (10101)2
4.阅读下列程序段,写出程序段运行后变量X 的值。(4%)
100 X1=3
X1:=3 ;
X2:=8 ;
FOR I:=1 TO 5 DO
BEGIN
X:=(X1+X2)*2 ;
X1:=X2 ;X2:=X ;
END;
WRITELN(‘X=’,X) ;
5.阅读下列程序段,写出程序运行后数组元素A1,A2,……A11中的值 。(6%)
A[1]:=1;
A[2]:=1 ; K:=1 ;
REPEAT
A[K+2]:=1 ;
FOR I:=K DOWNTO 2 DO
A[I]:=A[I] +A[I-1 ] ;
K:=K+1 ;
UNTIL K>=10 ;
6.已知:ACK(M,N)函数的计算公式如下: (4%)
N+1 M=0
ACK(M,N)= ACK(M-1,1) N=0
ACK(M-1,ACK(M,N-1) M≠0 且N≠0
请计算:ACK(1,2)与ACK(2,2)的值。
7.请写出对应计算如下算式的程序段:(4%)
Y=ANXN+AN-1XN-1+……A1X+A0
8.有N×N个数据组成如下方阵:(7%)
A11 A12 A13 …… A1N
A21 A22 A23 …… A2N
A31 A32 A33 …… A3N
…………
AN1 AN2 AN3 …… ANN
并已知: Aij = Aji
现将A11 ,A21,A22 ,A31 ,A32 ,A33 …存储在一维数组A[1],A[2],…A[(N*(N+1))/2] 中。
试问:任给i,j怎样求出K来,使得A[K]的值正好是Aij,请写出由i,j计算K值的表达式。
9.已知:A1,A2,……,A81 共有81个数,其中只有一个数比其它数大,要用最少的比较运算次数,把这个值大的数找出来(假设两个数比较一次能决定出大于、小于或等于这三种情况)请将以下算法补充完整:(9%)
第一步: S1 = A1 + A2 + …… + A27
S2 = A28 + A29 +……+ A54
第一次比较(S1,S2) :
S1 > S2 取 K=0
S1 < S2 取 K=27
S1 = S2 取 K=54
第二步: S1 = AK+1 + AK+2 + …… + AK+9
S2 = AK+10 + AK+11 +……+ AK+18
第二次比较(S1,S2) :
S1 > S2 取 K=
S1 < S2 取 K=
S1 = S2 取 K=
第三步: S1 = AK+1 + AK+2 + AK+3
S2 = AK+4 + AK+5 + AK+6
第三次比较(S1,S2) :
S1 > S2 取 K=
S1 < S2 取 K=
S1 = S2 取 K=
第四步: S1 = AK+1
S2 = AK+2
第四次比较(S1,S2) :
S1 > S2 为最大数
S1 < S2 为最大数,
S1 = S2 为最大数。
二.根据题目要求,补充完善以下程序:(56%)
1.[题 目] 15分(每空5分)
设有N个不同整数的数列:例如N=4时,有4个不同整数的数列为17,4,16,5。数列中的第1个数17,比它后面的三个数都大,则称数17的逆数为3。数列中的第2个数4比它后面的数都小,则称数4的逆数为0。同时记数列中全部逆数的和称为数列的逆数。上例中,数列17,4,16,5的逆数:为3+0+1+0=4。
[程序要求]:当给出N个不同整数的数列后,求出此数列的逆数。
[算法描述]:为求得上面问题的解,设置数组A:array[1..N] of Integer 和逆数计数器5,然后用一个二重循环求出数列的逆数。
[程 序]:
Const N=10;
Var i,j,s:integer;
A:array[1..N] of integer;
Begin
S:=0;
For I:=1 to n do read(a[I]);
For I:=1 to 1 do
For j:= 2 to n do
If a[I]>a[j] then 3 ;
Writeln('s=',s)
End.
2.[题 目] 20分(每空4分)
装球:设有n个盒子(n足够大,可装入任何数量的球),分别编号1,2,……。同时有k个小球(k>0),今将k 个小球装入到盒子中去。
装入规则如下:
第一个盒子不能为空。
装入必须严格按递增顺序进行。
例如,当k=8,n=6时,装入方法有1,2,5或1,3,4
在满足上面的两个条件下,要求有球的盒子尽可能多。
装完后,相邻盒子中球个数差的绝对值之和最小(未装的盒子不计)。
如上例中:
装入法1,2,5,则差的绝对值之和为2-1+5-2=4
装入法1,3,4,则差的绝对值之和为3-1+4-3=3
[程序要求]:给出k(k表示小球的个数)之后,求出满足上述四个条件的装入方法。
[算法描述]:设计一个数组A用数组元素代表盒子,然后依次装入小球。
[程序清单]
Const n=20;
Var i,j,k,l:integer;
A:array[1..n] of integer;
Begin
Readln(k);
1 ;
j:=1;
while 2 do begin
a[j]:=j; 3 ; j:=j+1
end;
l:=j-1;
while k>0 do begin
4 ;
k:=k-1;
l:=l-1;
end;
for I:=1 to 5 do
write(a[I]:4)
end.
3.[题 目] 21分(3+4+3+3+4+4)
积木游戏:设有n 个小木块排成一排,如下图:
……
游戏开始时,每个小木块向下的一面涂有红、黄、蓝三种颜色之中的一种(约定:0表示红色,1表示黄色,2表示兰色)。要求通过翻看与交换方式对小木块重新排列(翻看的规则为每个小木快只能看一次),最终成为下面的形状:
…… …… ……
红 蓝 黄
即相同颜色的木块排列在一起,设计一个翻看与交换的方案,使得用最少的交换次数实现上面的要求。
[算法描述]:翻看小木块时,可以从两端进行。
例如,设中间状态如下:
…… A …… B …… C ……
红 未翻过 蓝 黄
此时,可以从两个方向看,即从A或B处开始:
若看A则有三种可能性:
为红色,则不用交换
为兰色,交换一次,即A与B交换
为黄色,交换两次,即C与B交换一次,然后A与C再交换一次
此时,平均交换次数为1。
若看B,也有三种可能性:
为兰色,则不用交换
为红色,交换一次,即B与A交换。
为黄色,交换一次,即B与C交换。
此时,平均交换次数为2/3。
由此可见,从B处翻看直到游戏结束,次数最少符合题目要求。
[程 序]
Const n=20;
Var i,tem,r,b,y:integer;
a:array[1..n] of 0..2;
Begin
For i:=1 to n do read(a[i]);
r:=1; 1 ; y:=n;
while 2 do
if 3 then begin
tem:=a[r];a[r]:=a[b];a[b]:=tem;
r:=r+1
end
else if 4 then begin
tem:=a[b];a[b]:=a[y];a[y]:=tem;
5 ; 6 ;
end
else b:=b=1
for I:=1 to n do write(a[I]:3)
end.
同课章节目录
