人教版 高一物理 选修3-1 第一章 第2节 库仑定律(共22张PPT)
文档属性
| 名称 | 人教版 高一物理 选修3-1 第一章 第2节 库仑定律(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
杭州外国语学校
物理选修3-1
物理选修3-1
第一章 静电场
第一章 静电场
电荷及其守恒定律
复习巩固
【两种电荷】
【元电荷】
电荷量 称为元电荷.
——是 电荷量.
自然界存在 两种电荷,
带电体所带电荷的多少叫 .
符号 ;
单位 .
同种电荷 异种电荷 .
起电,
起电,
起电.
【起电方式】
——本质是 !
【电荷守恒定律】
电荷守恒定律适用于一切宏观和微观过程,是物理学中普遍的基本定律之一。
电荷量
Q或q
库仑(C)
正负
相互排斥
相互吸引
最小
摩擦
感应
接触
电子转移
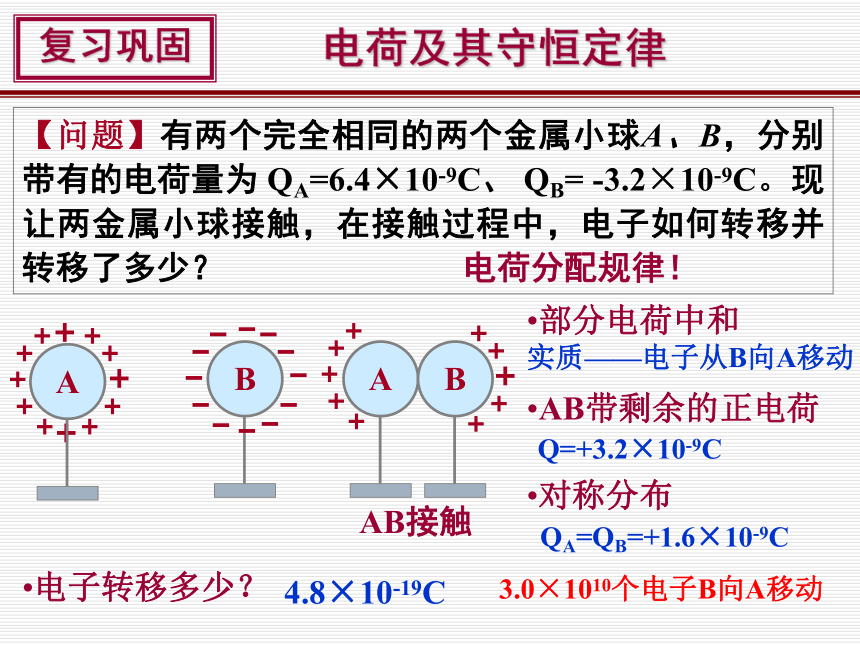
【问题】有两个完全相同的两个金属小球A、B,分别带有的电荷量为 QA=6.4×10-9C、 QB= -3.2×10-9C。现让两金属小球接触,在接触过程中,电子如何转移并转移了多少?
电荷分配规律!
部分电荷中和
实质——电子从B向A移动
AB带剩余的正电荷
对称分布
电子转移多少?
Q=+3.2×10-9C
QA=QB=+1.6×10-9C
4.8×10-19C
电荷及其守恒定律
复习巩固
3.0×1010个电子B向A移动
【问题】如图中A、B是两个不带电的相同的绝缘金属球,它们靠近带正电荷的金球C.在下列情况中,判断A、B两球的带电情况:
1、A、B接触后分开,再移去C;
2、A、B接触,先移去C后,再把AB分开;
3、A、B接触,用手指瞬间接触B后再移去C。
A
B
C
正电
负电
都不带电
都带负电
电荷及其守恒定律
复习巩固
新课题
定性实验——控制变量法
电荷之间的相互作用力
与带电体的电量有关
与带电体之间的距离有关
与带电体自身的大小及形状有关
与带电体所处的空间物质即介质有关
▲猜想:力的大小与哪些因素有关?
▲思想方法:
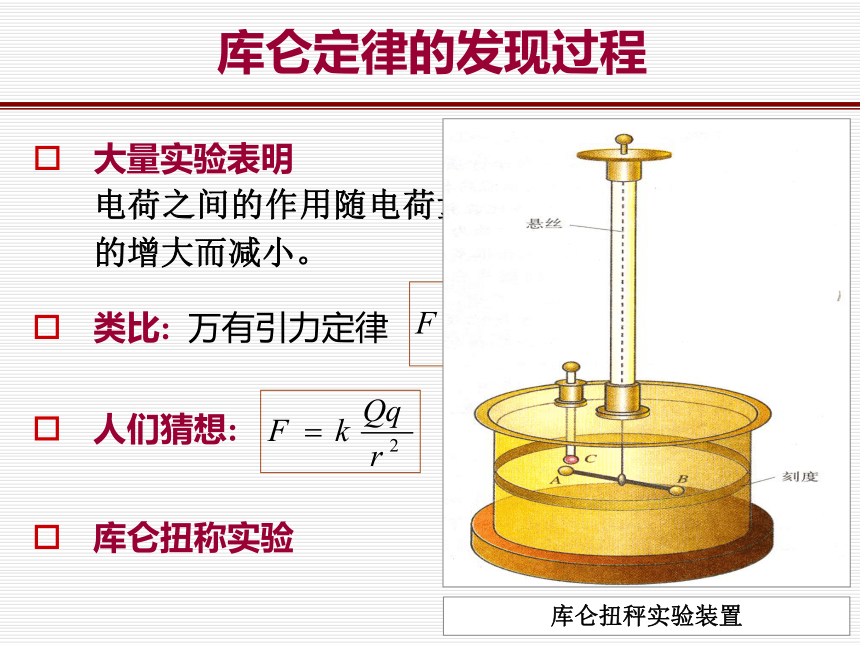
库仑定律的发现过程
大量实验表明
电荷之间的作用随电荷量的增大而增大,随距离的增大而减小。
类比: 万有引力定律
库仑扭称实验
人们猜想:
常量:
库 仑 定 律
公式:
适用条件:真空中的点电荷
▲真空中两个静止点电荷之间的相互作用力(叫静电力或库仑力),跟它们的电荷量的乘积成正比,跟它们间的距离的二次方成反比。作用力的方向在它们的连线上,同种电荷相互排斥,异种电荷相互吸引。
点电荷(理想模型)
——忽略带电体的大小:
L > > R
(空气中的点电荷近似适用)
遵循牛顿第三定律,力的平行四边形定则.
静电力:
【理解点电荷】
——只有电量,没有大小、形状的理想化模型
(1)点电荷是理想化的物理模型,实际上是不存在的.
(2)实际的带电体在本身的大小跟带电体间的距离相比小得多时可看作是点电荷
注意:是否可将带电体看作点电荷不是看它本身的尺寸大小。
如:一个半径是10cm的带电圆盘,如果考虑它和相距10m处的某个电子的作用力,就完全可以把它看作点电荷,而如果电子离带电圆盘只有1mm,那么这一带电圆盘就相当于一个无限大的带电平面。
——忽略带电体的大小!
又如:
典型例题
例:氢原子中电子绕核旋转,质子质量 mp = 1.67?10-27 kg , 电子质量 me= 9.11?10-31 kg , 在氢原子中它们之间的最短距离为5.3 ?10-10 m。试求电子与质子间的库仑力Fe与万有引力F引之比。
解:库仑力大小:
万有引力大小:
思考:
如若d=10cm,F=?
例:如图,A、B两个带电金属小球,半径为r=2cm,球心相距d=100cm,QA=2×10-6C,QB=10-6C。求他们之间的库仑力F?
典型例题
解:
上面解法对吗?
典型例题
例:两个可自由移动的点电荷分别放在A、B两处,如图所示A处电荷带正电Q1,B处电荷带负电Q2,且Q2=4Q1,另取一个可以自由移动的点电荷Q3放在AB直线上.欲使整个系统处于平衡状态,则:
A、Q3为负电荷,且放于A左方
B、Q3为负电荷,且放于B右方
C、Q3为正电荷,且放于AB之间
D、Q3为正电荷,且放于B右方
A正确
规律1:两同夹异
规律2:两大夹小
典型例题
例:两个完全一样的带电金属小球A和B相距较远,它们所带电量分别为2×10-5C和6×10-5C,将它们接触一下后放回原处,A、B之间的静电力变成原来的多少倍?
原来:
Q1=?2×10-5C
Q2=?6×10-5C
接触后:
(1)Q1′=+4×10-5C Q2′=+4×10-5C
(2)Q1′=-4×10-5C Q2′=-4×10-5C
(3)Q1′=+2×10-5C Q2′=+2×10-5C
(4)Q1′=-2×10-5C Q2′=-2×10-5C
典型例题
例:如图所示,等边三角形ABC,边长为L,在顶点A、B处有等量异种点电荷QA、QB,QA=+Q,QB=-Q,求在顶点C处带电量为2Q的点电荷QC所受的静电力。
解:
以QC为研究对象,分析QC受力情况。
**题目中没有明确QC电性,解答时就需考虑QC带正负电的两种情况。
(1)当QC为正电荷,受力情况:
解:
以QC为研究对象,分析QC受力情况。
QA对QC作用力(同种电荷相斥):
QB对QC作用力(异种电荷相吸):
∵QA=QB=Q ∴FA=FB
则:
,方向水平面向右。
(2)当QC为负电荷时,受力情况:
则:
,方向水平面向左。
例:如图所示,真空中两个相同的小球带有等量同种电荷,质量均为0.1g。分别用10cm长的绝缘细线悬挂于绝缘天花板的同一点,当平衡时B球偏离竖直方向600,A球竖直悬挂且与墙壁接触。求:
(1) 每个小球的带电量;
(2)墙壁受到的压力;
(3) 每条细线的拉力.
典型例题
第一步:确定研究对象
第二步:对研究对象进行受力分析
第三步:确定研究对象所处的状态遵循的规律
第四步:根据规律列方程求解
——静止不动(平衡状态),?F=0
【分析】
——A、B球
——列原始方程
对A:
对B:
其中:
解得:
对A、B球受力分析
例:如图所示, 在绝缘光滑水平面上的A、B两点分别放置质量m和2m的点电荷QA、QB。将两个点电荷同时释放,已知刚释放时QA的加速度是a,经过一段时间后(两电荷未相遇),QB的加速度也为a,且此时的速度大小为v。求:
(1)释放时B的加速度多大?
(2)释放后A、B做什么运动?v、a如何变化 ?
(3)当B的加速度为a时,A的加速度为多大?
典型例题
(2)变加速运动
v逐渐增大,a逐渐增大!
(3)2a
例:如图,已知A、B两相同的小球质量为m,带有相同的电量,绝缘细绳长为l,他们张开的夹角为θ。求两带电小球所带电量Q的大小。
典型例题
思考:
若A球电量增至2Q,哪个夹角大?
若A球质量增至2m,哪个夹角大?
典型例题
一样大
右边大
物体带电
电荷守恒定律
库仑定律
小 结
电荷及其守恒定律 库仑定律
库仑定律是电磁学的基本定律之一,它由法国物理学家库仑(1736-1806)在实验研究中于1785年发现.
你能初步谈谈库仑力和
万有引力的共同点和不同点吗?
万有引力定律 库仑定律
不同点 只有引力 既有引力又有斥力
天体间表现明显 微观带电粒子间表现明显
都是场力 万有引力场 电场
公式
条件 两质点之间 两点电荷之间
杭州外国语学校
物理选修3-1
物理选修3-1
第一章 静电场
第一章 静电场
电荷及其守恒定律
复习巩固
【两种电荷】
【元电荷】
电荷量 称为元电荷.
——是 电荷量.
自然界存在 两种电荷,
带电体所带电荷的多少叫 .
符号 ;
单位 .
同种电荷 异种电荷 .
起电,
起电,
起电.
【起电方式】
——本质是 !
【电荷守恒定律】
电荷守恒定律适用于一切宏观和微观过程,是物理学中普遍的基本定律之一。
电荷量
Q或q
库仑(C)
正负
相互排斥
相互吸引
最小
摩擦
感应
接触
电子转移
【问题】有两个完全相同的两个金属小球A、B,分别带有的电荷量为 QA=6.4×10-9C、 QB= -3.2×10-9C。现让两金属小球接触,在接触过程中,电子如何转移并转移了多少?
电荷分配规律!
部分电荷中和
实质——电子从B向A移动
AB带剩余的正电荷
对称分布
电子转移多少?
Q=+3.2×10-9C
QA=QB=+1.6×10-9C
4.8×10-19C
电荷及其守恒定律
复习巩固
3.0×1010个电子B向A移动
【问题】如图中A、B是两个不带电的相同的绝缘金属球,它们靠近带正电荷的金球C.在下列情况中,判断A、B两球的带电情况:
1、A、B接触后分开,再移去C;
2、A、B接触,先移去C后,再把AB分开;
3、A、B接触,用手指瞬间接触B后再移去C。
A
B
C
正电
负电
都不带电
都带负电
电荷及其守恒定律
复习巩固
新课题
定性实验——控制变量法
电荷之间的相互作用力
与带电体的电量有关
与带电体之间的距离有关
与带电体自身的大小及形状有关
与带电体所处的空间物质即介质有关
▲猜想:力的大小与哪些因素有关?
▲思想方法:
库仑定律的发现过程
大量实验表明
电荷之间的作用随电荷量的增大而增大,随距离的增大而减小。
类比: 万有引力定律
库仑扭称实验
人们猜想:
常量:
库 仑 定 律
公式:
适用条件:真空中的点电荷
▲真空中两个静止点电荷之间的相互作用力(叫静电力或库仑力),跟它们的电荷量的乘积成正比,跟它们间的距离的二次方成反比。作用力的方向在它们的连线上,同种电荷相互排斥,异种电荷相互吸引。
点电荷(理想模型)
——忽略带电体的大小:
L > > R
(空气中的点电荷近似适用)
遵循牛顿第三定律,力的平行四边形定则.
静电力:
【理解点电荷】
——只有电量,没有大小、形状的理想化模型
(1)点电荷是理想化的物理模型,实际上是不存在的.
(2)实际的带电体在本身的大小跟带电体间的距离相比小得多时可看作是点电荷
注意:是否可将带电体看作点电荷不是看它本身的尺寸大小。
如:一个半径是10cm的带电圆盘,如果考虑它和相距10m处的某个电子的作用力,就完全可以把它看作点电荷,而如果电子离带电圆盘只有1mm,那么这一带电圆盘就相当于一个无限大的带电平面。
——忽略带电体的大小!
又如:
典型例题
例:氢原子中电子绕核旋转,质子质量 mp = 1.67?10-27 kg , 电子质量 me= 9.11?10-31 kg , 在氢原子中它们之间的最短距离为5.3 ?10-10 m。试求电子与质子间的库仑力Fe与万有引力F引之比。
解:库仑力大小:
万有引力大小:
思考:
如若d=10cm,F=?
例:如图,A、B两个带电金属小球,半径为r=2cm,球心相距d=100cm,QA=2×10-6C,QB=10-6C。求他们之间的库仑力F?
典型例题
解:
上面解法对吗?
典型例题
例:两个可自由移动的点电荷分别放在A、B两处,如图所示A处电荷带正电Q1,B处电荷带负电Q2,且Q2=4Q1,另取一个可以自由移动的点电荷Q3放在AB直线上.欲使整个系统处于平衡状态,则:
A、Q3为负电荷,且放于A左方
B、Q3为负电荷,且放于B右方
C、Q3为正电荷,且放于AB之间
D、Q3为正电荷,且放于B右方
A正确
规律1:两同夹异
规律2:两大夹小
典型例题
例:两个完全一样的带电金属小球A和B相距较远,它们所带电量分别为2×10-5C和6×10-5C,将它们接触一下后放回原处,A、B之间的静电力变成原来的多少倍?
原来:
Q1=?2×10-5C
Q2=?6×10-5C
接触后:
(1)Q1′=+4×10-5C Q2′=+4×10-5C
(2)Q1′=-4×10-5C Q2′=-4×10-5C
(3)Q1′=+2×10-5C Q2′=+2×10-5C
(4)Q1′=-2×10-5C Q2′=-2×10-5C
典型例题
例:如图所示,等边三角形ABC,边长为L,在顶点A、B处有等量异种点电荷QA、QB,QA=+Q,QB=-Q,求在顶点C处带电量为2Q的点电荷QC所受的静电力。
解:
以QC为研究对象,分析QC受力情况。
**题目中没有明确QC电性,解答时就需考虑QC带正负电的两种情况。
(1)当QC为正电荷,受力情况:
解:
以QC为研究对象,分析QC受力情况。
QA对QC作用力(同种电荷相斥):
QB对QC作用力(异种电荷相吸):
∵QA=QB=Q ∴FA=FB
则:
,方向水平面向右。
(2)当QC为负电荷时,受力情况:
则:
,方向水平面向左。
例:如图所示,真空中两个相同的小球带有等量同种电荷,质量均为0.1g。分别用10cm长的绝缘细线悬挂于绝缘天花板的同一点,当平衡时B球偏离竖直方向600,A球竖直悬挂且与墙壁接触。求:
(1) 每个小球的带电量;
(2)墙壁受到的压力;
(3) 每条细线的拉力.
典型例题
第一步:确定研究对象
第二步:对研究对象进行受力分析
第三步:确定研究对象所处的状态遵循的规律
第四步:根据规律列方程求解
——静止不动(平衡状态),?F=0
【分析】
——A、B球
——列原始方程
对A:
对B:
其中:
解得:
对A、B球受力分析
例:如图所示, 在绝缘光滑水平面上的A、B两点分别放置质量m和2m的点电荷QA、QB。将两个点电荷同时释放,已知刚释放时QA的加速度是a,经过一段时间后(两电荷未相遇),QB的加速度也为a,且此时的速度大小为v。求:
(1)释放时B的加速度多大?
(2)释放后A、B做什么运动?v、a如何变化 ?
(3)当B的加速度为a时,A的加速度为多大?
典型例题
(2)变加速运动
v逐渐增大,a逐渐增大!
(3)2a
例:如图,已知A、B两相同的小球质量为m,带有相同的电量,绝缘细绳长为l,他们张开的夹角为θ。求两带电小球所带电量Q的大小。
典型例题
思考:
若A球电量增至2Q,哪个夹角大?
若A球质量增至2m,哪个夹角大?
典型例题
一样大
右边大
物体带电
电荷守恒定律
库仑定律
小 结
电荷及其守恒定律 库仑定律
库仑定律是电磁学的基本定律之一,它由法国物理学家库仑(1736-1806)在实验研究中于1785年发现.
你能初步谈谈库仑力和
万有引力的共同点和不同点吗?
万有引力定律 库仑定律
不同点 只有引力 既有引力又有斥力
天体间表现明显 微观带电粒子间表现明显
都是场力 万有引力场 电场
公式
条件 两质点之间 两点电荷之间
