人教版数学七年级下册5.2-5.3平行线复习讲义(3课时 无答案)
文档属性
| 名称 | 人教版数学七年级下册5.2-5.3平行线复习讲义(3课时 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 817.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级:初一 课 时 数: 3 学员姓名: 辅导科目:数学 学科教师:
授课类型 T同步( 平行线复习 )
授课日期及时段
教学内容
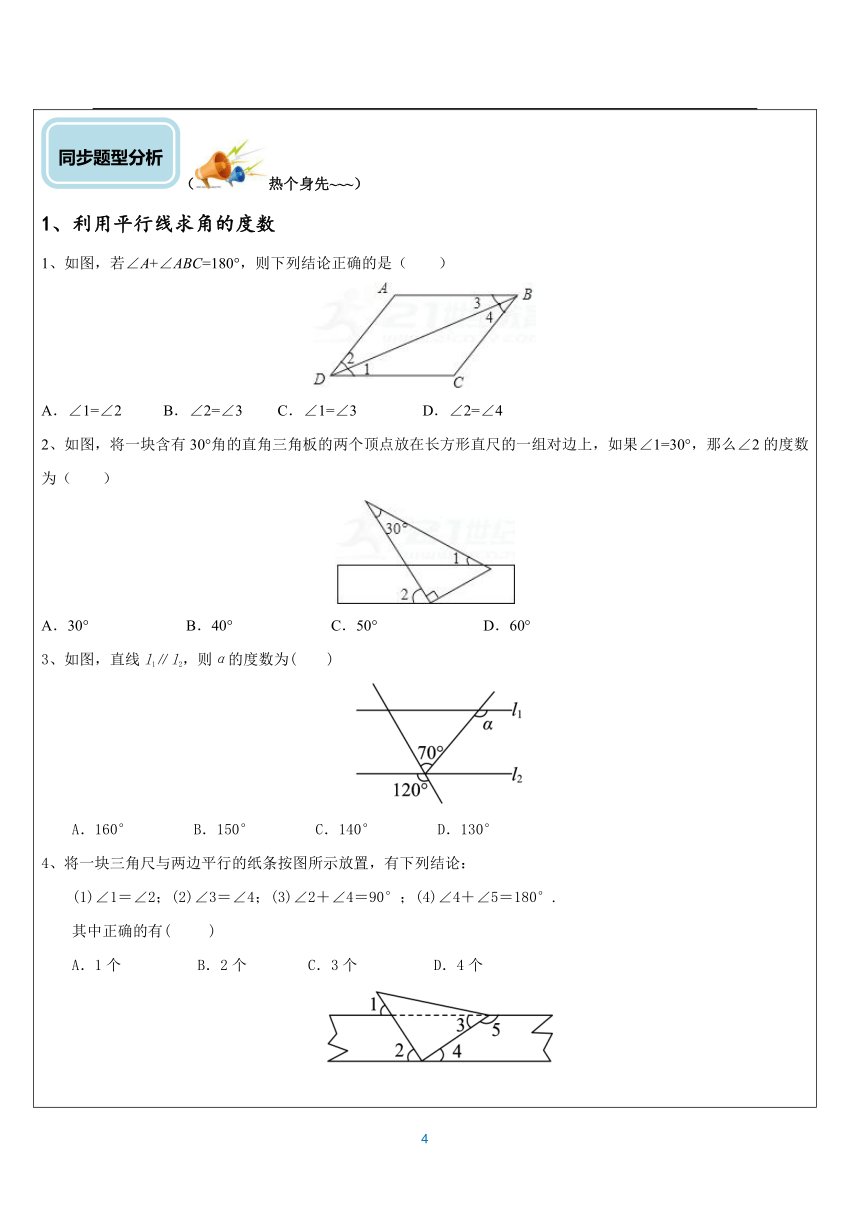
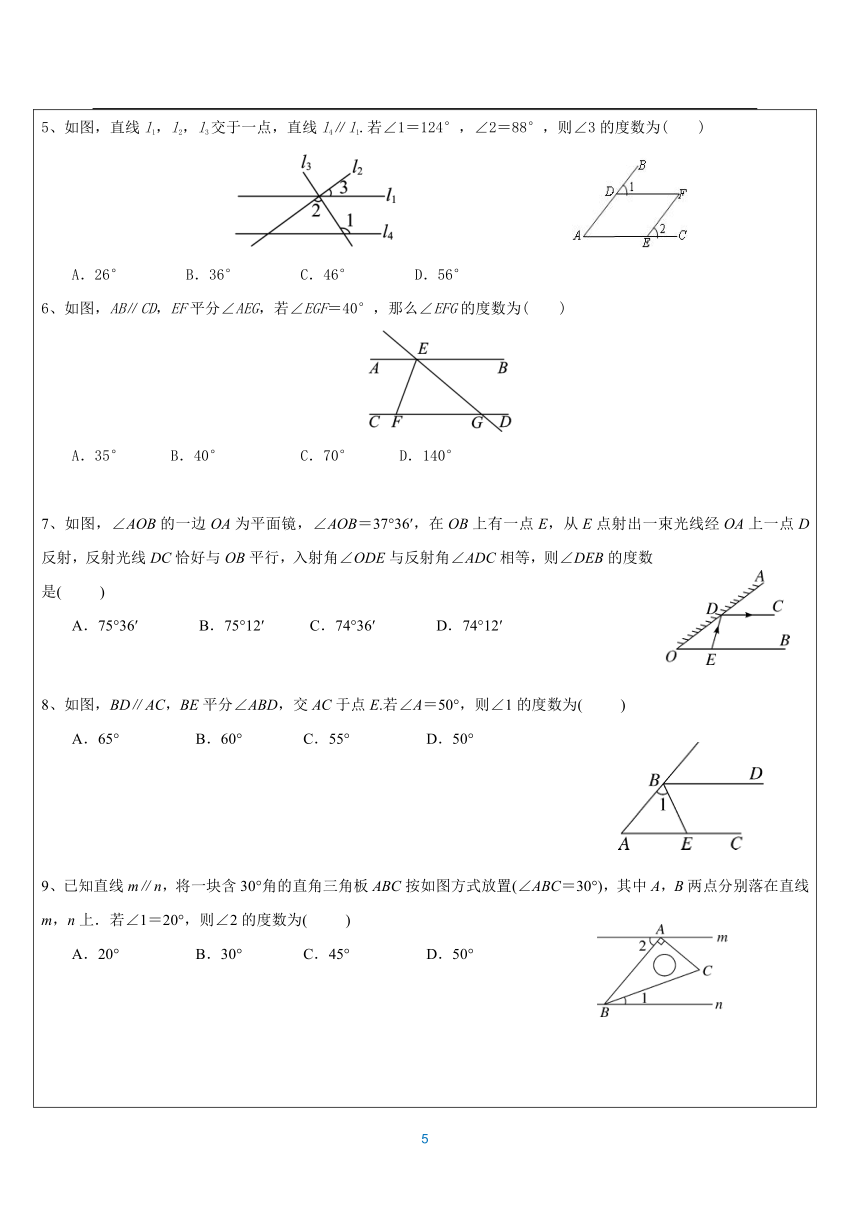
(热个身先~~~) 知识点一:平行线1.三线八角两条直线AB、CD与直线EF相交,交点分别为E、F,如图,则称直线AB、CD被直线EF所截,直线EF为截线.两条直线AB、CD被直线EF所截可得8个角,即所谓“三线八角”.(一)这八个角中有:(1)对顶角:∠1与∠3,∠2与∠4,∠5与∠7,∠6与∠8.(2)邻补角有:∠1与∠2,∠2与∠3,∠3与∠4,∠4与∠1,∠5与∠6,∠6与∠7, ∠7与∠8,∠8与∠5.(二)同位角,内错角,同旁内角:(1)同位角:两条直线被第三条直线所截,在二条直线的同侧,且在第三条直线的同旁的两个角叫同位角.如图中的∠1与∠5分别在直线AB、CD的上侧,又在第三条直线EF的右侧,所以∠1与∠5是同位角,它们的位置相同,在图中还有∠2与∠6,∠4与∠8,∠3与∠7也是同位角.(2)内错角:两条直线被第三条直线所截,在二条直线的内侧,且在第三条直线的两旁的两个角叫内错角.如上图中∠2与∠8在直线AB、CD的内侧(即AB、CD之间),且在EF的两旁,所以∠2与∠8是内错角.同理,∠3与∠5也是内错角.(3)同旁内角:两条直线被第三条直线所截,在两条直线的内侧,且在第三条直线的同旁的两个角叫同旁内角.如上图中的∠2与∠5在直线AB、CD内侧又在EF的同旁,所以∠2与∠5是同旁内角,同理,∠3与∠8也是同旁内角.因此,两条直线被第三条直线所截,共得4对同位角,2对内错角,2对同旁内角.2.平行线的定义(1)在同一平面内,不相交的两条直线叫做平行线.(2)平行线的定义包含三层意思: ①“在同一平面内”是前提条件; ②“不相交”是指两条直线没有交点;③平行线指的是”两条直线”,而不是两条射线或两条线段.(3)平行公理:经过一条直线外一点,有且只有一条直线与已知直线平行.(4)推论:(平行线的传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行。 也就是说:设a、b、c是三条直线,如果a//b,b//c,那么a//c. 3.平行线的判定:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简记为:同位角相等,两直线平行两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。 简记为:内错角相等,两直线平行两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。简记为:同旁内角互补,两直线平行 4.平行线的性质(1)两条平行线被第三条直线所截,同位角相等。 简记为:两直线平行, 同位角相等(2)两条平行线被第三条直线所截,内错角相等。 简记为:两直线平行,内错角相等(3)两条平行线被第三条直线所截,同旁内角互补。简记为:两直线平行,同旁内角互补 知识点二:命题、定理、证明和平移的性质1.命题的定义、分类及联系判断一件事情的语句叫做命题。命题分真命题和假命题。 真命题:如果题设成立,那么结论一定成立,这样的命题叫真命题。 假命题:题设成立时,不能保证结论一定成立的命题,这样的命题叫假命题。 经过推理证实得到的真命题叫做定理。定理都是真命题,而真命题不一定是定理。2.平移的性质:(1)平移是沿直线移动。(2)平移后得到的新图形与原图形的形状和大小完全相同。(3)新图形中的每一点,都是由原图形中的某一点移动得到的,这两个点是对应点,连接各组对应点的线段平行且相等。 (热个身先~~~) 1、利用平行线求角的度数1、如图,若∠A+∠ABC=180°,则下列结论正确的是( ) A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠42、如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果∠1=30°,那么∠2的度数为( )2-1-c-n-j-y A.30° B.40° C.50° D.60°3、如图,直线l1∥l2,则α的度数为( ) INCLUDEPICTURE "H:\\人教·数学·七下·学练考三校\\9QR44.EPS" \* MERGEFORMATINET A.160° B.150° C.140° D.130°4、将一块三角尺与两边平行的纸条按图所示放置,有下列结论: (1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°.其中正确的有( ) A.1个 B.2个 C.3个 D.4个 INCLUDEPICTURE "H:\\人教·数学·七下·学练考三校\\GC23.EPS" \* MERGEFORMATINET 5、如图,直线l1,l2,l3交于一点,直线l4∥l1.若∠1=124°,∠2=88°,则∠3的度数为( ) INCLUDEPICTURE "H:\\人教·数学·七下·学练考三校\\7RT133.EPS" \* MERGEFORMATINET A.26° B.36° C.46° D.56°6、如图,AB∥CD,EF平分∠AEG,若∠EGF=40°,那么∠EFG的度数为( ) A.35° B.40° C.70° D.140°7、如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,入射角∠ODE与反射角∠ADC相等,则∠DEB的度数是( ) A.75°36′ B.75°12′ C.74°36′ D.74°12′8、如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )A.65° B.60° C.55° D.50° 9、已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=20°,则∠2的度数为( ) A.20° B.30° C.45° D.50° 10、如图,AC∥DF,AB∥EF,若∠2=50°,则∠1的大小是( ) A. 60° B. 50° C. 40° D. 30° 11、如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=________. 12、如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=________. 13、如图,直线l1∥l2,∠1=20°,则∠2+∠3=________°. 14、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________°. 2、平行线的判定和性质的综合运用1、如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( ) A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°2、如图,能判断直线AB∥CD的条件是( ) A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠3+∠4=180°3、如图,能判定AB∥CD的条件是( ) A.∠A=∠ACD B.∠A=∠DCE C.∠B=∠ACB D.∠B=∠ACD4、如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )5、如图,下列条件,不能判断直线l1∥l2的是( ) A. ∠1=∠3 B. ∠1=∠4 C. ∠2+∠3=180° D. ∠3=∠56、如图,已知AB∥CD,∠1∶∠2∶∠3=1∶2∶3.(1)求∠1,∠2的度数; (2)求证:BA平分∠EBF. 7、如图,在四边形ABCD中,已知BE平分∠ABC,∠AEB=∠ABE,∠D=70°.(1)求证:AD∥BC; (2)求∠C的度数. 8、如图,∠BAD=∠DCB,∠BAC=∠DCA,试说明:AD∥BC. 9、如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD. 10、如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD. 11、如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由. 12、如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由. 13、如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么? 14、已知:如图9,AB∥CD,∠ABF=∠DCE。求证:∠BFE=∠FEC。 15、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数. 16、如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理(即证明) 17、如图,AE∥BD,∠1=3∠2,∠2=25°,求∠C. 18、已知DB∥FG∥EC,A是FG上一点,∠ABD=60°,∠ACE=36°,AP平分∠BAC,求:⑴∠BAC的大小;⑵∠PAG的大小. 19、如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求: (1)∠EDC的度数;(2)若∠BCD=n°,试求∠BED的度数.(用含n的式子表示) 20、如图,已知直线AB∥CD,∠A=∠C=100°,E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.21·世纪*教育网 (1)求证:AD∥BC; (2)求∠DBE的度数; (3)若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由. 题型二:命题、定理、证明1、对于命题“若a2>b2,则a>b.”下面四组关于a,b的值中,能说明这个命题是假命题的是( ) A.a=3,b=2 B.a=-3,b=2 C.a=3,b=-1 D.a=-1,b=32、下列命题是假命题的是( ) A.锐角小于它的补角 B.内错角相等 C.两点之间线段最短 D.同旁内角互补,两直线平行3、下列说法正确的是( ) A.“作线段CD=AB”是一个命题 B.过一点作已知直线的平行线有一条且只有一条 C.命题“若x=1,则x2=1”是真命题 D.命题“若>1,则a>b”是真命题4、“直角都相等”的题设是__________,结论是___________.5、下列命题中:①若|a|=b,则a=b;②若直线l1∥l2,l1∥l3,则l2∥l3;③同角的补角相等;④同位角相等,是真命题的有_____________(填序号).6、把下列命题写成“如果……那么……”的形式,并判断其真假. (1)等角的补角相等; (2)不相等的角不是对顶角; (3)相等的角是内错角. 题型三:平移1.如图6-S-1,若多边形的相邻两边互相垂直,则这个多边形的周长为( )图6-S-1 A.21 B.26 C.37 D.42 2.某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,主楼梯的宽为3米,其侧面如图6-S-2所示,则购买这种地毯至少需要________元. 图6-S-2 3.某医院用一个边长为1米的正方形材料制作一个红十字会的大型的“十”字标志,如图6-S-3,这个标志是由正方形的四个角上挖去四个相同的小正方形制作而成,则这个“十”字标志的周长为________米.图6-S-3 4.如图6-S-4,把正方形ABCD的对角线AC分成6段,以每一段为对角线作正方形,设正方形ABCD的边长为a,求图中6个小正方形的周长之和.图6-S-4 5.如图6-S-5,在宽为20 m,长为30 m的长方形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )图6-S-5 A.600 m2 B.551 m2 C.550 m2 D.500 m2 (你都掌握了没有呢~~~) 1、如图,AB∥EF∥CD,∠ABC=45°,∠CEF=155°,则∠BCE等于( ) A. 10° B. 15° C. 20° D. 25°2、如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转_____度.3、如图,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,且AB∶CD=1∶2,若三角形ABC的面积为6,则三角形BCD的面积为__________.?4、某江段江水流经B,C,D三点拐弯后与原来流向相同,如图,若∠ABC=120°,∠BCD=80°,则∠EDC=___________°.?5、如图,AC、BC分别平分∠DAB、∠ABE,且∠1与∠2互余, 则____∥____,理由是______.6、如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1=_______.7、如图,已知AC⊥AE,BD⊥BF,∠1=15°,∠2=15°,AE与BF平行吗?为什么? 8、AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么? 9、已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.(1)如图1,若∠E=80°,求∠BFD的度数.(2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.(3)若∠ABM=∠ABF,∠CDM=∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M. 10、如图,DE⊥AC于点E,BC⊥AC,CD⊥AB于点D,∠1=∠2,求证:GF⊥AB. 11、如图,∠ABC=∠ADC,BF,DE是∠ABC、∠ ADC的角平分线,∠1=∠2. 求证DC∥AB.
T同步平行线
同步题型分析
同步题型分析
课堂达标检测
