人教版七年级数学上册2.2《整式的加减——合并同类项》教学设计
文档属性
| 名称 | 人教版七年级数学上册2.2《整式的加减——合并同类项》教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 15:57:03 | ||
图片预览


文档简介
2.2整式的加减——合并同类项
教 学 过 程 教学环节 教 学 设 计 设计意图
创 设 情 境 一 问题1: 我们到动物园参观时,发现老虎与老虎关在一个笼子里,鹿与鹿关在另一个笼子里。为何不把老虎与鹿关在同一个笼子里呢? 问题2: (1)在日常生活中,你发现还有哪些事物也需要分类?能举出例子吗?如:垃圾、零钱、水果及各种产品分类.(2)生活中处处有分类的问题,在数学中也有分类的问题吗? 目的在于引发和提高学生学习的积极性,启发学生的探索欲望,加强学科联系,并注意联系生活,同时为本课学习做好准备和铺垫。
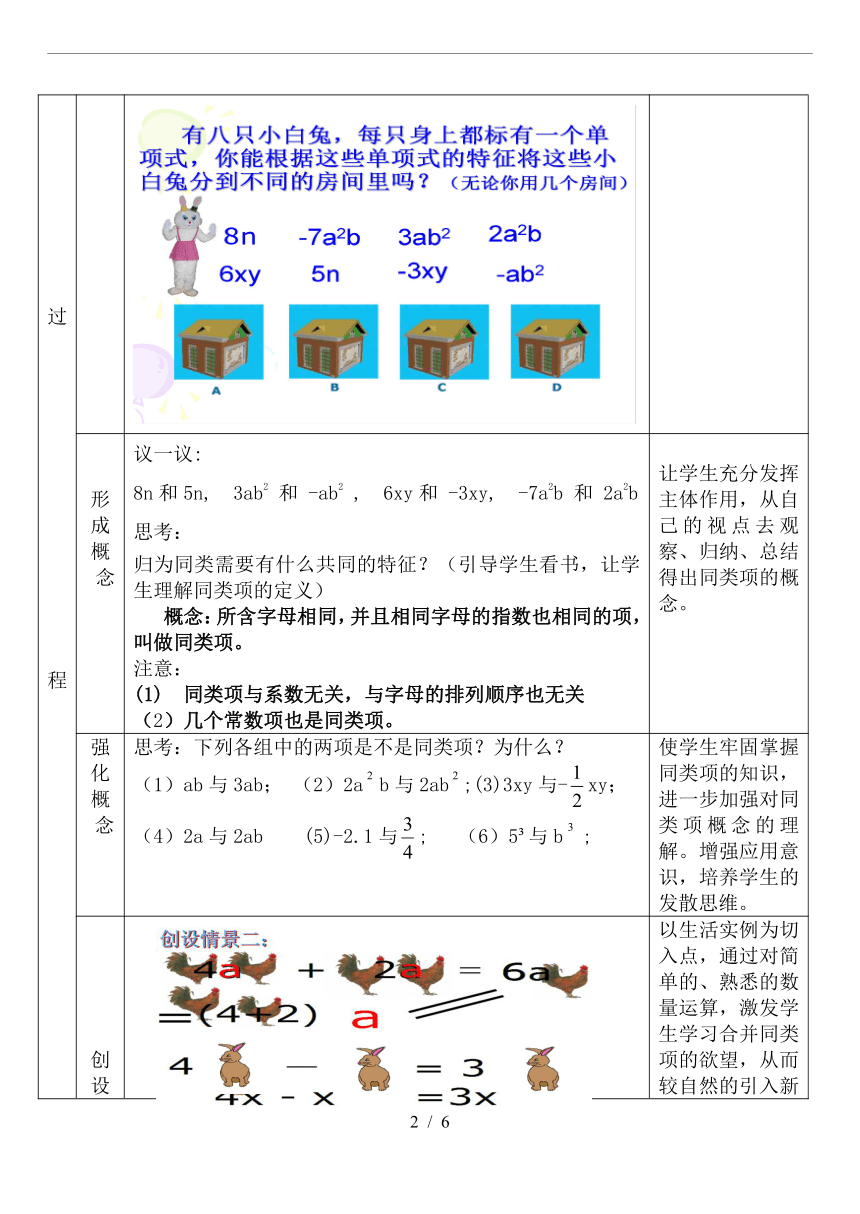
形 成 概 念 议一议: 8n和5n, 3ab2 和 -ab2 , 6xy和 -3xy, -7a2b 和 2a2b 思考: 归为同类需要有什么共同的特征?(引导学生看书,让学生理解同类项的定义) 概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项。 注意:(1) 同类项与系数无关,与字母的排列顺序也无关 (2)几个常数项也是同类项。 让学生充分发挥主体作用,从自己的视点去观察、归纳、总结得出同类项的概念。
强 化 概 念 思考:下列各组中的两项是不是同类项?为什么? (1)ab与3ab; (2)2ab与2ab;(3)3xy与-xy; (4)2a与2ab (5)-2.1与; (6)5?与b; 使学生牢固掌握同类项的知识,进一步加强对同类项概念的理解。增强应用意识,培养学生的发散思维。
创 设 情 景 二 如果一个多项式中含有同类项,那么常常把同类项合并起来,使结果得到简化,那么怎样才能把同类项合并起来呢?请同学们思考下面的问题?问题1: 3ab+5ab=_______理由是________ -4xy2+2xy2=_______ 理由是_______ -3a+2b= 理由是_______问题2: 不在一起的同类项能否将同类项结合在一起?为什么? 例如:试化简多项式3xy-4xy-3+5xy+2xy+5 解:3xy-4xy-3+5xy+2xy+5--------------找出 (用不同的标志把同类项标出来!) =3xy+5xy-4xy+2xy-3+5 ----------加法交换律 =(3xy+5xy)+(-4xy+2xy)+(-3+5)--加法结合律 =(3+5)xy+(-4+2)xy+2 ---------乘法分配律逆用 =8 xy-2 xy+2 ----------合并 运用加法交换律和结合律将同类项结合在一起,原多项式的值不变。 合并同类项:
把同类项合并成一项就叫做合并同类项探讨:合并同类项后,所得项的系数、字母以及字母的指数与合并前各同类项的系数、字母及字母的指数有什么联系? 以生活实例为切入点,通过对简单的、熟悉的数量运算,激发学生学习合并同类项的欲望,从而较自然的引入新课题。
层 层 追 问 引 出 法 则 例题:合并下列各式中的同类项: 1).2ab-3ab+ab 2).a-ab+ab+ab-ab+b 3).6a-5b+2ab+b-6a 解:1).2ab-3ab+ab=(2-3+)ab=- ab 方法是:(1)系数:各项系数相加作为新的系数。 (2)字母以及字母的指数不变。 2).-2ab+2ab+ab-ab--------------找出 =-2ab+ab+2ab-ab ----------加法交换律 =(-2ab+ab)+(2ab-ab)--加法结合律 =(-2+1)ab +(2-1)ab---------乘法分配律逆用 = -ab+ ab----------合并 3).6a-5b+2ab+b-6a =(6a-6a)+(-5b+b)+2ab-------没有同类项照抄下来 =-4 b+2ab思考:合并同类项的步骤是怎样?合并同类项法则: 同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。注意:(1)用画线的方法标出各多项式中的同类项,以减少运算的错误。 (2)移项时要带着原来的符号一起移动。 (3)两个同类项的系数互为相反数时,合并同类项,结果为零。如:-3ab2+3ab2=(-3+3)ab2=0×ab2=0。(4)多项式中只有同类项才能合并,不是同类项不能合并。 分解难度,设计过渡问题,使学生能自然的感受法则的探索过程。
合 并 同 类 项 的 步 骤 合并同类项一般步骤:1、找出同类项 2、交换律 3、结合律 4、分配律逆用 5、合并 注意: (1)用画线的方法标出各多项式中的同类项,以减少运算的错误。 (2)移项时要带着原来的符号一起移动。 (3)两个同类项的系数互为相反数时,合并同类项,结果为零。 以一道例题的训练为桥梁来得出合并同类项的一般步骤。体现新课程中以学生为主,注重学生参与的理念。
巩 固 法 则 尝 试 训 练 尝试训练:(1)3x+x; (2)xy- xy; (3)4a?+3b?+2ab-4a?-4b? 请你完成: (1) 3x-8x-9x (2) 5a2+2ab-4a2-4ab (3) 2x-7y-5x+11y-1知识延伸: 已知与是同类项,求m.n的值。 提高练习: 1.如果2a2bn+1与-4amb3是同类项,则m=____,n=____; 2.若5xy2+axy2=-2xy2,则a=___; 3.在6xy-3x2-4x2y-5yx2+x2中没有同类项 的项是______ 小组共练互批,及时纠错,共同提高 小组讨论 进一步让学生巩固基本知识,渗透数学分类思想;使知识结构更完善。
课堂小结 教师 总结 谈一谈:通过这节课的学习你学到了什么? 你想提醒你的小伙伴们注意哪些问题?
布 置 作 业 必做题:1、在下列代数式中,指出哪些是同类项。 2x2 ,0 ,-3x ,-x2y ,(x+y)2 ,xy2, x2y ,6x , -x2y , 0.5 , -x2 ,2(x+y)2 ;2、合并同类项 ①3y+2y ②3b-3a3+1+a3-2b ③2y+6y+2xy-5 ④6mn+4m2n-3mn+5mn23、填充: (1)在( )内填上相应字母,使得2( )3( )2与5x2y3是同类项; (2)若x3ym和xny2是同类项,则 = ; (3)若(n-3)x2yz和x2yz是同类项,则 ; 选做题:你会玩下面的两个数字游戏吗?游戏步骤:任写一个两位数 交换十位和个位数,得到一个新两位数 求这两个两位数的和。做完后观察结果,你发现了什么?这个规律对任何一个两位数都成立吗?如果成立,如何说明呢?你能自编一个数学游戏吗?这个游戏有什么特点?与同伴一起玩这个游戏。 必做题进一步巩固学生所学知识,及时发现和弥补知识缺陷,起到课后巩固和反馈作用。在第二项作业中利用游戏为下面的学习埋下了伏笔,这样就可以激发学生想象力,启迪创新,应用意识。
对下类水果进行分类:
同
类
项
相同字母的指数一样
所含字母一样
②交换律
③结合律
④分配律
①找出
A.系数相加减;
B.字母和字母的指数不变。
⑤合并:
合并
法则
要点
PAGE / NUMPAGES
