2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试(有详细答案)
文档属性
| 名称 | 2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试(有详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 21:09:56 | ||
图片预览




文档简介
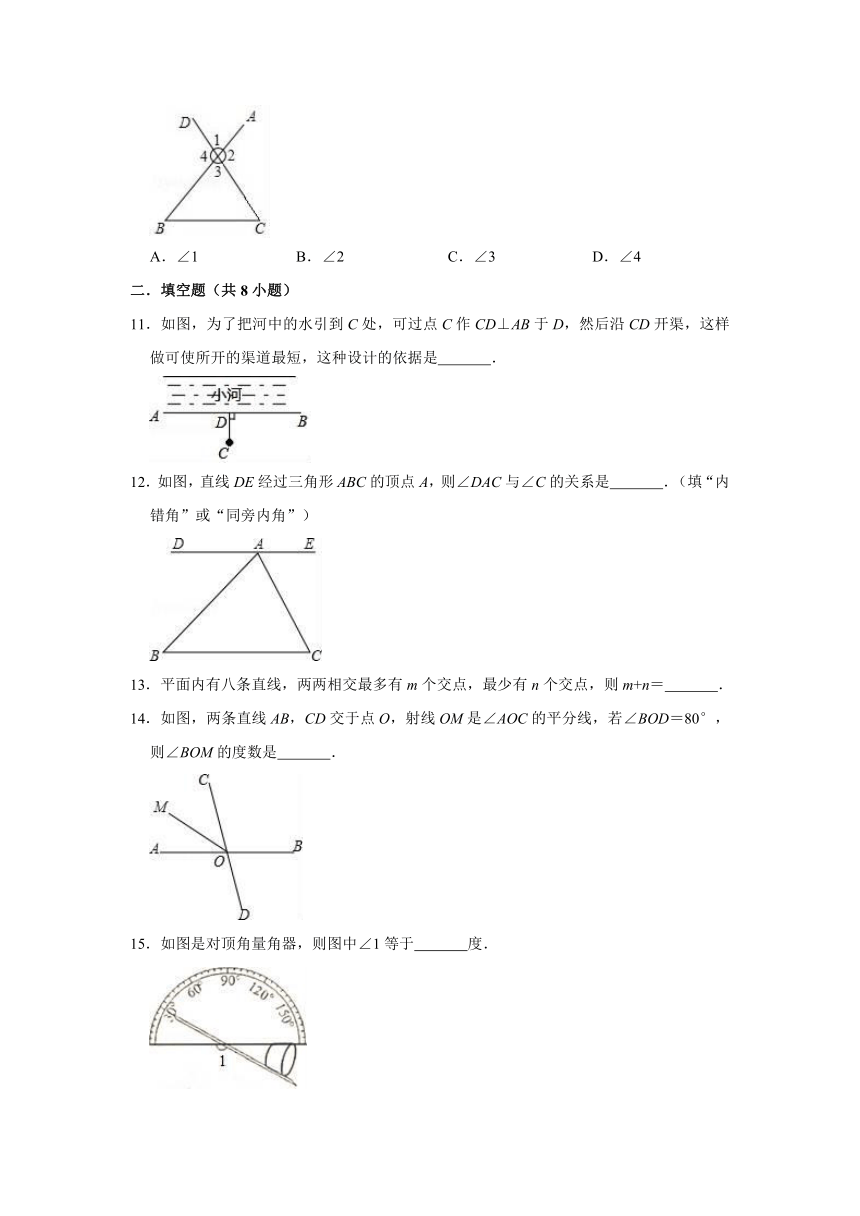
2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试
一.选择题(共10小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,直线m、n相交于一点,∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3理由是( )
A.如果两个角的和等于90°,那么这两个角互余
B.同角(等角)的余角相等
C.如果两个角的和等于180°,那么这两个角互补
D.同角(等角)的补角相等
3.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是( )
A.PA B.PB C.PC D.PD
4.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.①②④ D.①④
5.如图,直线AB⊥直线CD,垂足为O,直线EF经过点O,若∠BOE=35°,则∠FOD=( )
A.35° B.45° C.55° D.125°
6.如图所示,与∠A是同旁内角的角共有( )个.
A.2 B.3 C.4 D.5
7.如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠A与∠B是同旁内角
C.∠2与∠3是内错角 D.∠A与∠3是同位角
8.如图直线AB、CD相交于点O,∠1=∠2,若∠AOE=140°,则∠AOC的度数为( )
A.50° B.60° C.70° D.80°
9.若点P为直线l外一定点,点A为直线l上一定点,且PA=2,点P到直线l的距离为d,则d的取值范围为( )
A.0<d<2 B.d=2或d>2 C.0<d<2或d=0 D.0<d<2或d=2
10.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
二.填空题(共8小题)
11.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是 .
12.如图,直线DE经过三角形ABC的顶点A,则∠DAC与∠C的关系是 .(填“内错角”或“同旁内角”)
13.平面内有八条直线,两两相交最多有m个交点,最少有n个交点,则m+n= .
14.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是 .
15.如图是对顶角量角器,则图中∠1等于 度.
16.如图所示,直线AB、CD交于点E,EF⊥CD于点E,∠AEF=55.75°,则∠BED= °.
17.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
18.如图,BC⊥AC,BC=12,AC=9,AB=15,则点C到线段AB的距离是 .
三.解答题(共7小题)
19.已知点A,B,C如图所示,根据要求完成下列各题.
(1)画直线BC,线段AB和射线CA.
(2)过点A画BC的垂线段AD,垂足为D,并量出点A到直线BC的距离为 cm.(以答题纸为测量依据,结果精确到0.1cm).
20.如图.已知直线AB、CD相交于点O,射线OF和射线OD分别平分∠AOF和∠BOF且∠AOC=30°,求∠EOF.
21.如图所示,已知直线AB和CD相交于点O.∠COE是直角,OF平分∠AOE.
(1)∠AOC与∠BOD的大小关系是 ,判断的依据是 ;
(2)若∠COF=32°,求∠BOD的度数.
22.如图,直线AB与CD相交于O,OE是∠COB的平分线,OE⊥OF,∠AOD=74°,求∠COF的度数.
23.如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°﹣∠AOC= °.
∵OD是∠BOC的角平分线,
∴∠COD= ∠BOC.( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE﹣∠COD= °.
24.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
25.如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=∠COF.
(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
参考答案与试题解析
一.选择题(共10小题)
1.解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选:D.
2.解:∵∠1+∠2=180°,∠1+∠3=180°,
∴∠2=∠3(同角(等角)的补角相等).
故选:D.
3.解:从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是PB,
故选:B.
4.解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;
图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.
故选:C.
5.解:∵直线AB⊥直线CD,
∴∠BOC=∠AOD=90°,
∵∠BOE=35°,
∴∠FOD=∠COE=90°﹣35°=55°.
故选:C.
6.解:与∠A是同旁内角的有:∠ABC、∠ADC、∠ADE,∠AED,共有4个.
故选:C.
7.解:A、∠C与∠1是内错角,故此选项不符合题意;
B、∠A与∠B是同旁内角,故此选项不符合题意;
C、∠2与∠3是邻补角,故此选项符合题意;
D、∠A与∠3是同位角,故此选项不符合题意;
故选:C.
8.解:∵∠AOE=140°,
∴∠2=180°﹣140°=40°,
∵∠1=∠2,
∴∠1=40°,
∴∠DOB=80°,
∴∠AOC=80°,
故选:D.
9.解:∵点P为直线l外一定点,点A为直线l上一定点,且PA=2,
∴点P到直线l的距离d的取值范围为:0<d<2或d=2,
故选:D.
10.解:如图,∠B的内错角是∠4
故选:D.
二.填空题(共8小题)
11.解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.
故答案为:垂线段最短.
12.解:由图可知:∠DAC与∠C的关系是同旁内角,
故答案为:同旁内角
13.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:8×(8﹣1)÷2=28,
即m=28;
则m+n=28+1=29.
故答案为:29.
14.解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
15.解:根据对顶角相等,得零件的锥角等于30°,
∴∠1=180°﹣30°=150°.
故答案为:150.
16.解:∵EF⊥CD,
∴∠CEF=90°,
∴∠AEC=∠CEF﹣∠AEF=90°﹣55.75°=34.25°,
∴∠BED=∠AEC=34.25°.
故答案为:34.25°.
17.解:①∠A与∠1是同位角,此结论正确;
②∠A与∠B是同旁内角,此结论正确;
③∠4与∠1不是内错角,此结论错误;
④∠1与∠3是内错角,此结论错误;
故答案为:①②.
18.解:∵92+122=152,
∴AC2+BC2=AB2,
∴∠C=90°,
设点C到AB的距离是h, AC?BC=AB?h,
解得:h=7.2.
故答案为:7.2.
三.解答题(共7小题)
19.解:(1)如图所示:
(2)经测量AD=1.8cm,
故答案为:1.8.
20.解:∵射线OF和射线OD分别平分∠AOF和∠BOF,
∴∠EOF=∠AOF,∠DOF=∠BOF,
∴∠EOF+∠DOF=(∠AOF+∠BOF)=∠AOB=×180°,
即∠EOD=90°,
∵∠AOC=30°,
∴∠AOE=180°﹣∠AOC﹣∠EOD=180°﹣30°﹣90°=60°,
∵∠EOF=∠AOE=60°.
21.解:(1)相等;对顶角相等.
(2)∵∠COE=90°,∠COF=32°
∴∠EOF=∠COE﹣∠COF=90°﹣32°=58°
∵OF平分∠AOE
∴∠AOF=∠EOF=58°
∴∠AOC=∠AOF﹣∠COF=58°﹣32°=26°
∴∠BOD=∠AOC=26°.
22.解:∵∠AOD=70°,
∴∠BOC=70°,
∵OE是∠COB的平分线,
∴∠COE=∠COB=37°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°﹣37°=53°.
23.解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°﹣∠AOC=130°.
∵OD是∠BOC的角平分线,
∴∠COD=∠BOC.(角平分线的定义)
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE=90°.(垂直的定义)
∴∠DOE=∠COE﹣∠COD=25°.
故答案为:130,,角平分线的定义,90,垂直的定义,25.
24.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
25.解:(1)∵∠COM=120°,
∴∠DOF=120°,
∵OG平分∠DOF,
∴∠FOG=60°;
(2)与∠FOG互为同位角的角是∠BMF;
(3)∵∠COM=120°,
∴∠COF=60°,
∵∠EMB=∠COF,
∴∠EMB=30°,
∴∠AMO=30°.
一.选择题(共10小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,直线m、n相交于一点,∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3理由是( )
A.如果两个角的和等于90°,那么这两个角互余
B.同角(等角)的余角相等
C.如果两个角的和等于180°,那么这两个角互补
D.同角(等角)的补角相等
3.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是( )
A.PA B.PB C.PC D.PD
4.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.①②④ D.①④
5.如图,直线AB⊥直线CD,垂足为O,直线EF经过点O,若∠BOE=35°,则∠FOD=( )
A.35° B.45° C.55° D.125°
6.如图所示,与∠A是同旁内角的角共有( )个.
A.2 B.3 C.4 D.5
7.如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠A与∠B是同旁内角
C.∠2与∠3是内错角 D.∠A与∠3是同位角
8.如图直线AB、CD相交于点O,∠1=∠2,若∠AOE=140°,则∠AOC的度数为( )
A.50° B.60° C.70° D.80°
9.若点P为直线l外一定点,点A为直线l上一定点,且PA=2,点P到直线l的距离为d,则d的取值范围为( )
A.0<d<2 B.d=2或d>2 C.0<d<2或d=0 D.0<d<2或d=2
10.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
二.填空题(共8小题)
11.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是 .
12.如图,直线DE经过三角形ABC的顶点A,则∠DAC与∠C的关系是 .(填“内错角”或“同旁内角”)
13.平面内有八条直线,两两相交最多有m个交点,最少有n个交点,则m+n= .
14.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是 .
15.如图是对顶角量角器,则图中∠1等于 度.
16.如图所示,直线AB、CD交于点E,EF⊥CD于点E,∠AEF=55.75°,则∠BED= °.
17.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
18.如图,BC⊥AC,BC=12,AC=9,AB=15,则点C到线段AB的距离是 .
三.解答题(共7小题)
19.已知点A,B,C如图所示,根据要求完成下列各题.
(1)画直线BC,线段AB和射线CA.
(2)过点A画BC的垂线段AD,垂足为D,并量出点A到直线BC的距离为 cm.(以答题纸为测量依据,结果精确到0.1cm).
20.如图.已知直线AB、CD相交于点O,射线OF和射线OD分别平分∠AOF和∠BOF且∠AOC=30°,求∠EOF.
21.如图所示,已知直线AB和CD相交于点O.∠COE是直角,OF平分∠AOE.
(1)∠AOC与∠BOD的大小关系是 ,判断的依据是 ;
(2)若∠COF=32°,求∠BOD的度数.
22.如图,直线AB与CD相交于O,OE是∠COB的平分线,OE⊥OF,∠AOD=74°,求∠COF的度数.
23.如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°﹣∠AOC= °.
∵OD是∠BOC的角平分线,
∴∠COD= ∠BOC.( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE﹣∠COD= °.
24.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
25.如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=∠COF.
(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
参考答案与试题解析
一.选择题(共10小题)
1.解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选:D.
2.解:∵∠1+∠2=180°,∠1+∠3=180°,
∴∠2=∠3(同角(等角)的补角相等).
故选:D.
3.解:从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是PB,
故选:B.
4.解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;
图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.
故选:C.
5.解:∵直线AB⊥直线CD,
∴∠BOC=∠AOD=90°,
∵∠BOE=35°,
∴∠FOD=∠COE=90°﹣35°=55°.
故选:C.
6.解:与∠A是同旁内角的有:∠ABC、∠ADC、∠ADE,∠AED,共有4个.
故选:C.
7.解:A、∠C与∠1是内错角,故此选项不符合题意;
B、∠A与∠B是同旁内角,故此选项不符合题意;
C、∠2与∠3是邻补角,故此选项符合题意;
D、∠A与∠3是同位角,故此选项不符合题意;
故选:C.
8.解:∵∠AOE=140°,
∴∠2=180°﹣140°=40°,
∵∠1=∠2,
∴∠1=40°,
∴∠DOB=80°,
∴∠AOC=80°,
故选:D.
9.解:∵点P为直线l外一定点,点A为直线l上一定点,且PA=2,
∴点P到直线l的距离d的取值范围为:0<d<2或d=2,
故选:D.
10.解:如图,∠B的内错角是∠4
故选:D.
二.填空题(共8小题)
11.解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.
故答案为:垂线段最短.
12.解:由图可知:∠DAC与∠C的关系是同旁内角,
故答案为:同旁内角
13.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:8×(8﹣1)÷2=28,
即m=28;
则m+n=28+1=29.
故答案为:29.
14.解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
15.解:根据对顶角相等,得零件的锥角等于30°,
∴∠1=180°﹣30°=150°.
故答案为:150.
16.解:∵EF⊥CD,
∴∠CEF=90°,
∴∠AEC=∠CEF﹣∠AEF=90°﹣55.75°=34.25°,
∴∠BED=∠AEC=34.25°.
故答案为:34.25°.
17.解:①∠A与∠1是同位角,此结论正确;
②∠A与∠B是同旁内角,此结论正确;
③∠4与∠1不是内错角,此结论错误;
④∠1与∠3是内错角,此结论错误;
故答案为:①②.
18.解:∵92+122=152,
∴AC2+BC2=AB2,
∴∠C=90°,
设点C到AB的距离是h, AC?BC=AB?h,
解得:h=7.2.
故答案为:7.2.
三.解答题(共7小题)
19.解:(1)如图所示:
(2)经测量AD=1.8cm,
故答案为:1.8.
20.解:∵射线OF和射线OD分别平分∠AOF和∠BOF,
∴∠EOF=∠AOF,∠DOF=∠BOF,
∴∠EOF+∠DOF=(∠AOF+∠BOF)=∠AOB=×180°,
即∠EOD=90°,
∵∠AOC=30°,
∴∠AOE=180°﹣∠AOC﹣∠EOD=180°﹣30°﹣90°=60°,
∵∠EOF=∠AOE=60°.
21.解:(1)相等;对顶角相等.
(2)∵∠COE=90°,∠COF=32°
∴∠EOF=∠COE﹣∠COF=90°﹣32°=58°
∵OF平分∠AOE
∴∠AOF=∠EOF=58°
∴∠AOC=∠AOF﹣∠COF=58°﹣32°=26°
∴∠BOD=∠AOC=26°.
22.解:∵∠AOD=70°,
∴∠BOC=70°,
∵OE是∠COB的平分线,
∴∠COE=∠COB=37°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°﹣37°=53°.
23.解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°﹣∠AOC=130°.
∵OD是∠BOC的角平分线,
∴∠COD=∠BOC.(角平分线的定义)
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE=90°.(垂直的定义)
∴∠DOE=∠COE﹣∠COD=25°.
故答案为:130,,角平分线的定义,90,垂直的定义,25.
24.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
25.解:(1)∵∠COM=120°,
∴∠DOF=120°,
∵OG平分∠DOF,
∴∠FOG=60°;
(2)与∠FOG互为同位角的角是∠BMF;
(3)∵∠COM=120°,
∴∠COF=60°,
∵∠EMB=∠COF,
∴∠EMB=30°,
∴∠AMO=30°.
