人教版 数学九年级下册 第28章锐角三角函数复习——考点整合课件(共16张PPT)
文档属性
| 名称 | 人教版 数学九年级下册 第28章锐角三角函数复习——考点整合课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
null
人教版九年级数学下册
第二十八章 锐角三角函数
锐角三角函数复习课
考点整合专训
null
复习备用
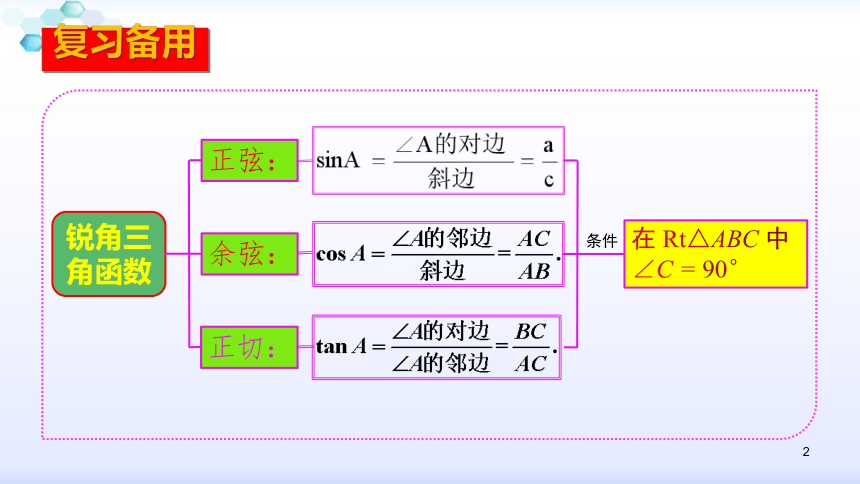
锐角三角函数
正弦:
正切:
在 Rt△ABC 中∠C = 90°
余弦:
条件
null
复习备用
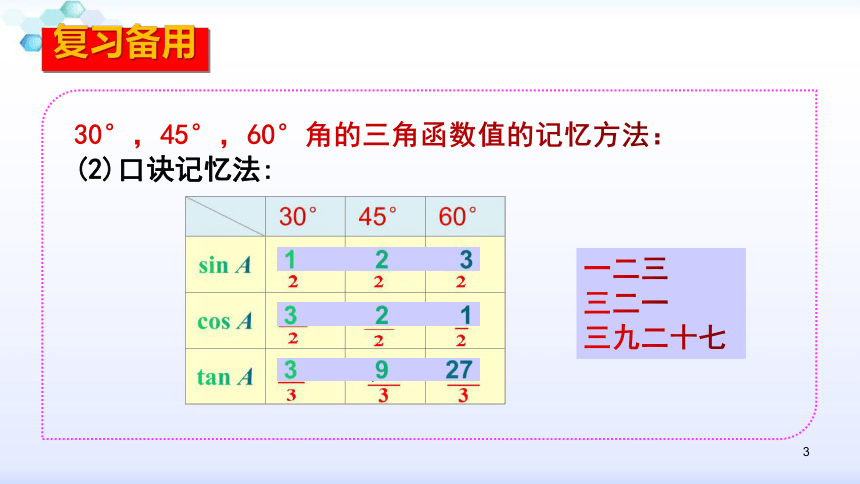
30°,45°,60°角的三角函数值的记忆方法:
(2)口诀记忆法:
一二三
三二一
三九二十七
null
复习备用
(2)两锐角之间的关系:
∠A+∠B=90°
(3)边角之间的关系:
(1)三边之间的关系:
a2+b2=c2
上述(3)中的A都可以换成B,同时把a,b互换.
直角三角形五个元素之间的关系:
解直角三角形:
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
本本章主要学习锐角三角函数的定义、锐角三角函数值、解直角三角形以及解直角三角形的实际应用,重点考查运用解直角三角形的知识解决一些几何图形中的应用和实际应用、是中考的必考内容.
主要考点可概括为:
两个概念,一个运算,两个应用,两个技巧.
null
中考分析
考点概括
null
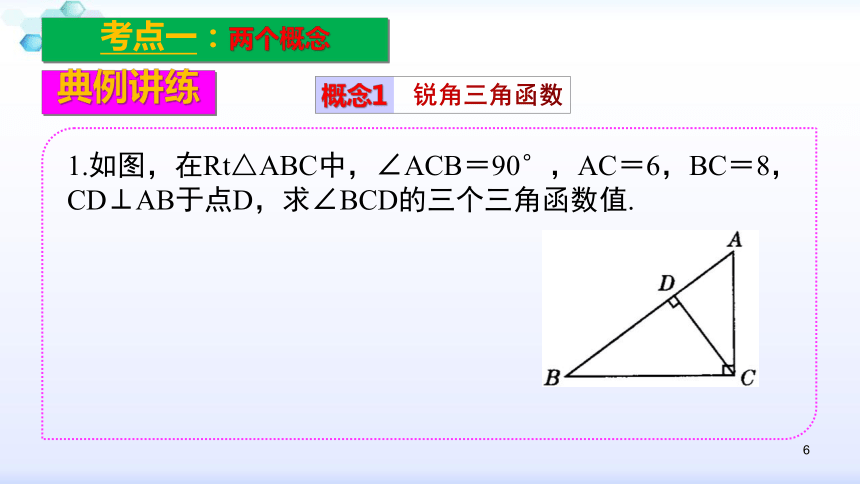
考点一:两个概念
典例讲练
1.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D,求∠BCD的三个三角函数值.
概念1
锐角三角函数
null
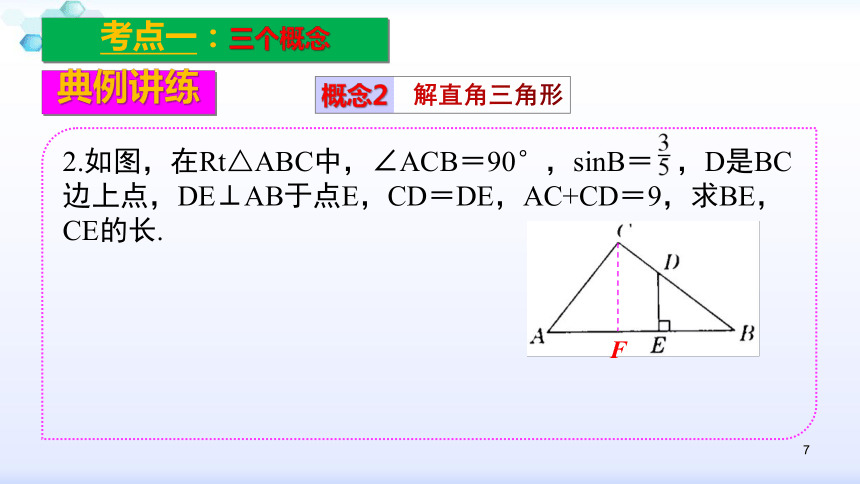
考点一:三个概念
概念2
解直角三角形
2.如图,在Rt△ABC中,∠ACB=90°,sinB= ,D是BC边上点,DE⊥AB于点E,CD=DE,AC+CD=9,求BE,CE的长.
典例讲练
F
null
考点二:一个运算
典例讲练
3.计算
(1)tan30°sin60°+cos230°-sin245°tan45°;
一个运算
特殊角的三角函数值与实数运算
考点三:两个应用
应用1
解直角三角形在学科内的应用
4.如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a
(1)当点P在线段BC上时(点P与点B,C都
不重合)试用含a的代数式表示CE的长.
null
典例讲练
考点三:两个应用
应用1
解直角三角形在学科内的应用
(2)当a=3时,连接DF,试判断四边形APFD的形状并说明理由;
(3)当tan∠PAE= 时,求a的值.
null
典例讲练
考点三:两个应用
应用2
解直角三角形的实际应用
5.如图,自来水厂A和村庄B在小河l 的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,
B位于南偏东24.5°方向,向东前行1200m,
到达点Q处,测得A位于北偏西49°方向,
B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由
(2)求A,B间的距离(参考数据:cos41°≈0.75)
null
典例讲练
考点三:两个应用
应用2
解直角三角形的实际应用
6.如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.
(结果用含非特殊角的三角函数和
根式表示即可)
null
典例讲练
F
null
典例讲练
考点四:两个技巧
技巧1
“化斜为直”构造直角三角形的技巧
7.如图,在△ABC中,∠A=30°tanB= ,AC=2√3,
求AB的长.
null
典例讲练
考点四:两个技巧
技巧2
“割补法”构造直角三角形求解的技巧
8.如图,已知四边形ABCD,∠ABC=120°,AD⊥AB,CD⊥BC、AB=30√3,BC=50√3,求四边形ABCD的面积(要求:用分割法和补形法两种方法求解).
null
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
null
1.《能力》单元测;
作业布置
null
人教版九年级数学下册
第二十八章 锐角三角函数
锐角三角函数复习课
考点整合专训
null
复习备用
锐角三角函数
正弦:
正切:
在 Rt△ABC 中∠C = 90°
余弦:
条件
null
复习备用
30°,45°,60°角的三角函数值的记忆方法:
(2)口诀记忆法:
一二三
三二一
三九二十七
null
复习备用
(2)两锐角之间的关系:
∠A+∠B=90°
(3)边角之间的关系:
(1)三边之间的关系:
a2+b2=c2
上述(3)中的A都可以换成B,同时把a,b互换.
直角三角形五个元素之间的关系:
解直角三角形:
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
本本章主要学习锐角三角函数的定义、锐角三角函数值、解直角三角形以及解直角三角形的实际应用,重点考查运用解直角三角形的知识解决一些几何图形中的应用和实际应用、是中考的必考内容.
主要考点可概括为:
两个概念,一个运算,两个应用,两个技巧.
null
中考分析
考点概括
null
考点一:两个概念
典例讲练
1.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D,求∠BCD的三个三角函数值.
概念1
锐角三角函数
null
考点一:三个概念
概念2
解直角三角形
2.如图,在Rt△ABC中,∠ACB=90°,sinB= ,D是BC边上点,DE⊥AB于点E,CD=DE,AC+CD=9,求BE,CE的长.
典例讲练
F
null
考点二:一个运算
典例讲练
3.计算
(1)tan30°sin60°+cos230°-sin245°tan45°;
一个运算
特殊角的三角函数值与实数运算
考点三:两个应用
应用1
解直角三角形在学科内的应用
4.如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a
(1)当点P在线段BC上时(点P与点B,C都
不重合)试用含a的代数式表示CE的长.
null
典例讲练
考点三:两个应用
应用1
解直角三角形在学科内的应用
(2)当a=3时,连接DF,试判断四边形APFD的形状并说明理由;
(3)当tan∠PAE= 时,求a的值.
null
典例讲练
考点三:两个应用
应用2
解直角三角形的实际应用
5.如图,自来水厂A和村庄B在小河l 的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,
B位于南偏东24.5°方向,向东前行1200m,
到达点Q处,测得A位于北偏西49°方向,
B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由
(2)求A,B间的距离(参考数据:cos41°≈0.75)
null
典例讲练
考点三:两个应用
应用2
解直角三角形的实际应用
6.如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.
(结果用含非特殊角的三角函数和
根式表示即可)
null
典例讲练
F
null
典例讲练
考点四:两个技巧
技巧1
“化斜为直”构造直角三角形的技巧
7.如图,在△ABC中,∠A=30°tanB= ,AC=2√3,
求AB的长.
null
典例讲练
考点四:两个技巧
技巧2
“割补法”构造直角三角形求解的技巧
8.如图,已知四边形ABCD,∠ABC=120°,AD⊥AB,CD⊥BC、AB=30√3,BC=50√3,求四边形ABCD的面积(要求:用分割法和补形法两种方法求解).
null
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
null
1.《能力》单元测;
作业布置
