2020春华东师大版八下数学17.2函数的图象课件(2课时 26张)
文档属性
| 名称 | 2020春华东师大版八下数学17.2函数的图象课件(2课时 26张) |  | |
| 格式 | zip | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 17:56:36 | ||
图片预览








文档简介
课件26张PPT。教学课件
数学 八年级下册 华东师大版
第17章 函数及其图象
17.2 函数的图象
第1课时 平面直角坐标系创设情境 明确目标同学们,你们喜欢旅游吗?假如你到了某
一个城市旅游,那么你应怎样确定旅游景
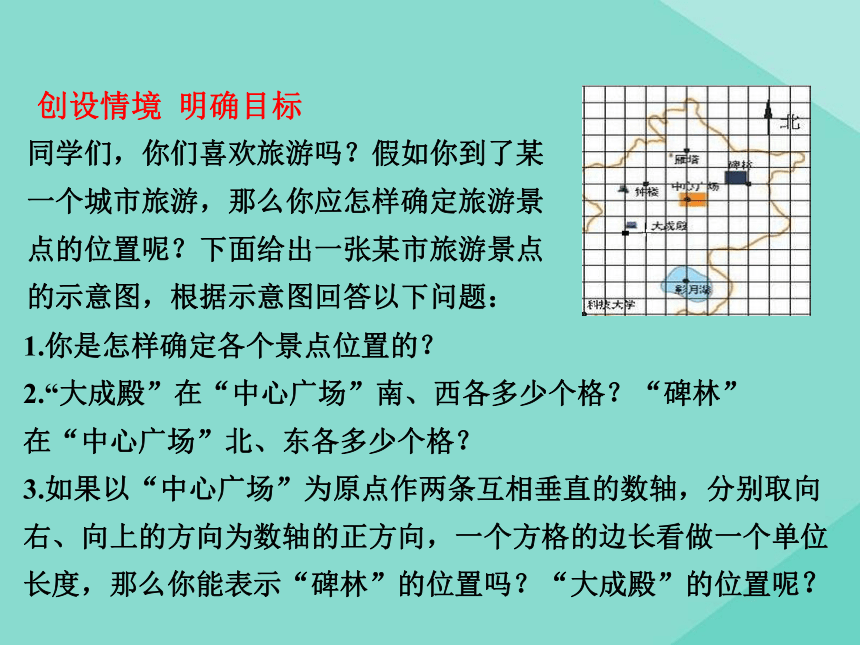
点的位置呢?下面给出一张某市旅游景点
的示意图,根据示意图回答以下问题:
1.你是怎样确定各个景点位置的?
2.“大成殿”在“中心广场”南、西各多少个格?“碑林”
在“中心广场”北、东各多少个格?
3.如果以“中心广场”为原点作两条互相垂直的数轴,分别取向
右、向上的方向为数轴的正方向,一个方格的边长看做一个单位
长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?在上一节课,我们已经学习了
许多确定位置的方法,这个问
题中,大家看用哪种方法比较
合适?今天这节课我们就来学
习这个问题。阅读教材,回答下列问题:1. 平面上 组成平面直角坐标系, ,叫x轴(横轴),取向 为正方向, ,叫y轴(纵轴),取向 为正方向。两轴的交点是 。这个平面叫 平面。2. 如何划分象限?
两条互相垂直且有公共原点的数轴 水平的数轴右上铅直的数轴原点坐标合作探究 达成目标探究点一:平面直角坐标系写出如图所示的六边形ABCDEF各个顶点的坐标解:A(-2,0), B(0,-3), C(3,-3), D(4,0), E(3,3), F(0,3)探究点二:由点写坐标、由坐标描点例题2.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3)。
观察所描出的图形,它像什么?xABCDGEFo连接起来的图形像“房子”1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。归纳 概括纵坐标等于 0横坐标等于 0纵坐标相同 横坐标相同 如图所示的笑脸中,
(1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。
(2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。各象限内点的坐标符号特征:
第一象限(+,+) 第二象限(-,+)
第三象限(-,-) 第四象限(+,-)总结梳理 达成目标1.认识并能画出平面直角坐标系。
2.在给定的直角坐标系中,由点的位置写出它的坐标,
由坐标描点。
3.横(纵)坐标相同的点的直线平行于y轴(垂直于
x轴);连接纵(横)坐标相同的点的直线平行于x轴
(平行于y轴)。
4.x轴上点的纵坐标为0;y轴上点的横坐标为0。
5.各个象限内的点的坐标特征是:
第一象限(+,+),第二象限(-,+),
第三象限(-,-),第四象限(+,-)。第17章 函数及其图象
17.2 函数的图象
第2课时 1、 汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。s = 60t解析法表示函数解析式主要能反映数量关系列表法表示函数表格主要能反映对应关系 2、 下表是某种股票一周内周一至周五的收盘价。 12 12.5 12.9 12.45 12.75 3、下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。41424t/小时8T/℃0图象法表示函数图象主要能反映什么?-3 变化规律表示函数关系的方法:1、解析法:准确地反映了函数与自变量之间的数量关系。2、列表法:具体地反映了函数与自变量的数值对应关系。3、图象法:直观地反映了函数随自变量的变化而变化的规律。归纳例 一水库的水位在近5小时内持续上涨,下表记录了
这5小时的水位高度。(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式,并画出函数图像。
(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式。 由记录表观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的变化规律可以表示为:
y=0.05t+10 (0 ≤t ≤5)
(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?y=0.05×7+10 =10.35 故2小时后,预计水位高10.35米。 1、 张老师从家里乘汽车去学校用了1小时,汽车的速度为30千米/时,在学校办事用了2小时,骑自行车经过3小时回到家。在直角坐标系中,用x轴表示时间,单位是时,用y轴表示路程,单位是千米,请你大致画出张老师这次去学校办事再返回家的路线图。x/小时y/千米012345-1-210203040672 .李华和弟弟进行百米赛跑,李华比弟弟跑得快,如果两人同时起跑,李华肯定赢.现在李华让弟弟先跑若干米,图中,分别表示两人的路程与李华追赶弟弟的时间的关系,由图中信息可知,下列结论中正确的是( ) .
A.李华先到达终点 B.弟弟的速度是8米/秒
C.弟弟先跑了10米 D.弟弟的速度是10米/秒B3、周末小明一家乘出租车前往离家8千米的公园,出租车的收费标准如下:(1)写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系。
(2)小明带了10元钱,够不够付到公园的车费,为什么?解:(1)从图象中观察得知:自变量X的取值范围是:0≤x≤5(2)从图象中观察得知:当 x = 3 时,y 有最小值,最小值 y = 2.5(3)从图象中观察得知:y 随着 x 的增大而减小。4、中考实战甲,乙两同学骑自行车从A地沿同一条路到B地,已知
乙比甲先出发.他们离出发地的距离s/km和骑行时间
t/h之间的函数关系如图所示,给出下列说法:
A.他们都骑了20km;
B.乙在途中停留了0.5h;
C.甲和乙两人同时到达目的地;
D.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )Bs/kmt/hA.1个B.2个D.4个C.3个甲乙龟兔赛跑龟兔赛跑的故事:
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,
当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已
经来不及了,乌龟先到达了终点……现在用 S1 和 S2
分别表示乌龟、兔子所走的路程,t为时间,则下列
图象中,能够表示S 和t之间的函数关系式的是( )ABDCC1、一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了,如图所示的各图能基本反映亮亮这一天(0—24时)的体温变化情况是( )C2.已知某一函数的图象如图所示,根据图象回答下列问题:(1)确定自变量的取值范围;解:自变量的取值范围是-4≤X≤4.(2)求当x=-4,-2,4时y的值是多少?解:y的值分别是2, -2,0.(3)求当y=0,4时x的值是多少?解:当y=0时,x的值是-3,-1或4;当y=4时,x=1.5.(4)当x取何值时y的值最大?当x取何值时y的值最小?解:当x=1.5时,y的值最大,值为4,当x=-2时,y的值最小,值为-2。(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
数学 八年级下册 华东师大版
第17章 函数及其图象
17.2 函数的图象
第1课时 平面直角坐标系创设情境 明确目标同学们,你们喜欢旅游吗?假如你到了某
一个城市旅游,那么你应怎样确定旅游景
点的位置呢?下面给出一张某市旅游景点
的示意图,根据示意图回答以下问题:
1.你是怎样确定各个景点位置的?
2.“大成殿”在“中心广场”南、西各多少个格?“碑林”
在“中心广场”北、东各多少个格?
3.如果以“中心广场”为原点作两条互相垂直的数轴,分别取向
右、向上的方向为数轴的正方向,一个方格的边长看做一个单位
长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?在上一节课,我们已经学习了
许多确定位置的方法,这个问
题中,大家看用哪种方法比较
合适?今天这节课我们就来学
习这个问题。阅读教材,回答下列问题:1. 平面上 组成平面直角坐标系, ,叫x轴(横轴),取向 为正方向, ,叫y轴(纵轴),取向 为正方向。两轴的交点是 。这个平面叫 平面。2. 如何划分象限?
两条互相垂直且有公共原点的数轴 水平的数轴右上铅直的数轴原点坐标合作探究 达成目标探究点一:平面直角坐标系写出如图所示的六边形ABCDEF各个顶点的坐标解:A(-2,0), B(0,-3), C(3,-3), D(4,0), E(3,3), F(0,3)探究点二:由点写坐标、由坐标描点例题2.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3)。
观察所描出的图形,它像什么?xABCDGEFo连接起来的图形像“房子”1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。归纳 概括纵坐标等于 0横坐标等于 0纵坐标相同 横坐标相同 如图所示的笑脸中,
(1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。
(2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。各象限内点的坐标符号特征:
第一象限(+,+) 第二象限(-,+)
第三象限(-,-) 第四象限(+,-)总结梳理 达成目标1.认识并能画出平面直角坐标系。
2.在给定的直角坐标系中,由点的位置写出它的坐标,
由坐标描点。
3.横(纵)坐标相同的点的直线平行于y轴(垂直于
x轴);连接纵(横)坐标相同的点的直线平行于x轴
(平行于y轴)。
4.x轴上点的纵坐标为0;y轴上点的横坐标为0。
5.各个象限内的点的坐标特征是:
第一象限(+,+),第二象限(-,+),
第三象限(-,-),第四象限(+,-)。第17章 函数及其图象
17.2 函数的图象
第2课时 1、 汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。s = 60t解析法表示函数解析式主要能反映数量关系列表法表示函数表格主要能反映对应关系 2、 下表是某种股票一周内周一至周五的收盘价。 12 12.5 12.9 12.45 12.75 3、下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。41424t/小时8T/℃0图象法表示函数图象主要能反映什么?-3 变化规律表示函数关系的方法:1、解析法:准确地反映了函数与自变量之间的数量关系。2、列表法:具体地反映了函数与自变量的数值对应关系。3、图象法:直观地反映了函数随自变量的变化而变化的规律。归纳例 一水库的水位在近5小时内持续上涨,下表记录了
这5小时的水位高度。(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式,并画出函数图像。
(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式。 由记录表观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的变化规律可以表示为:
y=0.05t+10 (0 ≤t ≤5)
(2)据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?y=0.05×7+10 =10.35 故2小时后,预计水位高10.35米。 1、 张老师从家里乘汽车去学校用了1小时,汽车的速度为30千米/时,在学校办事用了2小时,骑自行车经过3小时回到家。在直角坐标系中,用x轴表示时间,单位是时,用y轴表示路程,单位是千米,请你大致画出张老师这次去学校办事再返回家的路线图。x/小时y/千米012345-1-210203040672 .李华和弟弟进行百米赛跑,李华比弟弟跑得快,如果两人同时起跑,李华肯定赢.现在李华让弟弟先跑若干米,图中,分别表示两人的路程与李华追赶弟弟的时间的关系,由图中信息可知,下列结论中正确的是( ) .
A.李华先到达终点 B.弟弟的速度是8米/秒
C.弟弟先跑了10米 D.弟弟的速度是10米/秒B3、周末小明一家乘出租车前往离家8千米的公园,出租车的收费标准如下:(1)写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系。
(2)小明带了10元钱,够不够付到公园的车费,为什么?解:(1)从图象中观察得知:自变量X的取值范围是:0≤x≤5(2)从图象中观察得知:当 x = 3 时,y 有最小值,最小值 y = 2.5(3)从图象中观察得知:y 随着 x 的增大而减小。4、中考实战甲,乙两同学骑自行车从A地沿同一条路到B地,已知
乙比甲先出发.他们离出发地的距离s/km和骑行时间
t/h之间的函数关系如图所示,给出下列说法:
A.他们都骑了20km;
B.乙在途中停留了0.5h;
C.甲和乙两人同时到达目的地;
D.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )Bs/kmt/hA.1个B.2个D.4个C.3个甲乙龟兔赛跑龟兔赛跑的故事:
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,
当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已
经来不及了,乌龟先到达了终点……现在用 S1 和 S2
分别表示乌龟、兔子所走的路程,t为时间,则下列
图象中,能够表示S 和t之间的函数关系式的是( )ABDCC1、一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了,如图所示的各图能基本反映亮亮这一天(0—24时)的体温变化情况是( )C2.已知某一函数的图象如图所示,根据图象回答下列问题:(1)确定自变量的取值范围;解:自变量的取值范围是-4≤X≤4.(2)求当x=-4,-2,4时y的值是多少?解:y的值分别是2, -2,0.(3)求当y=0,4时x的值是多少?解:当y=0时,x的值是-3,-1或4;当y=4时,x=1.5.(4)当x取何值时y的值最大?当x取何值时y的值最小?解:当x=1.5时,y的值最大,值为4,当x=-2时,y的值最小,值为-2。(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
