2020春华东师大版八下数学18.2平行四边形的判定课件(2课时 26张)
文档属性
| 名称 | 2020春华东师大版八下数学18.2平行四边形的判定课件(2课时 26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览






文档简介
课件26张PPT。教学课件
数学 八年级下册 华东师大版
第18章 平行四边形
18.2 平行四边形的判定
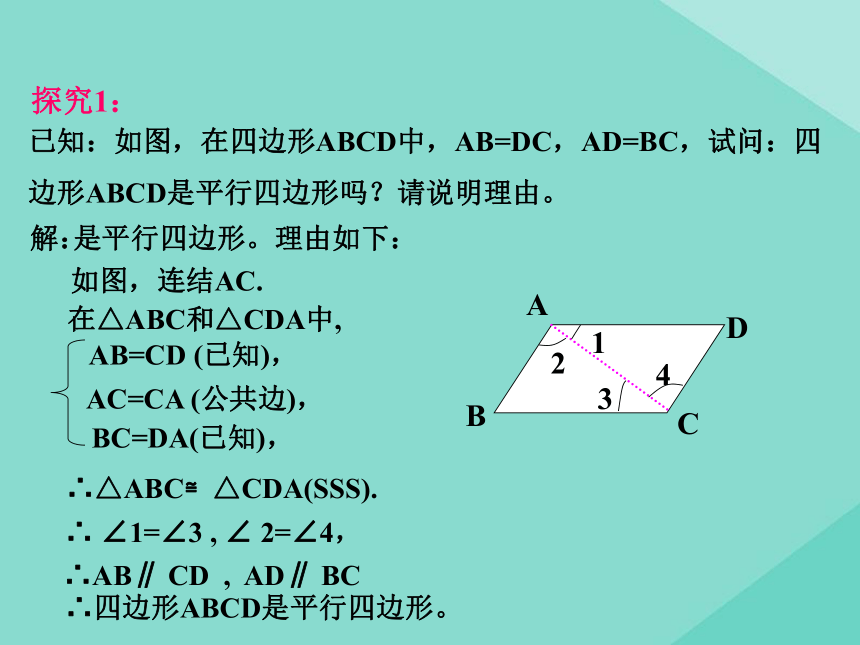
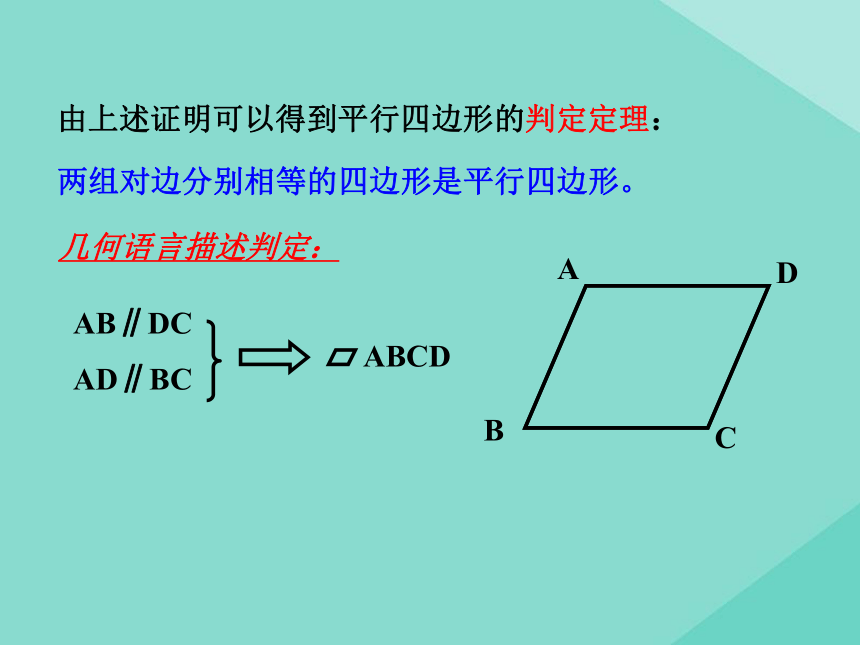
第1课时知识点回顾定义:有两组对边分别平行的四边形叫做平行四边形.性质: 通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?创设情境,引入新课探究1:已知:如图,在四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:如图,连结AC.AB=CD (已知),AC=CA (公共边),BC=DA(已知),∴△ABC≌△CDA(SSS).在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4,∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:探究2已知:如图,四边形ABCD中,AB=CD, AB∥CD,
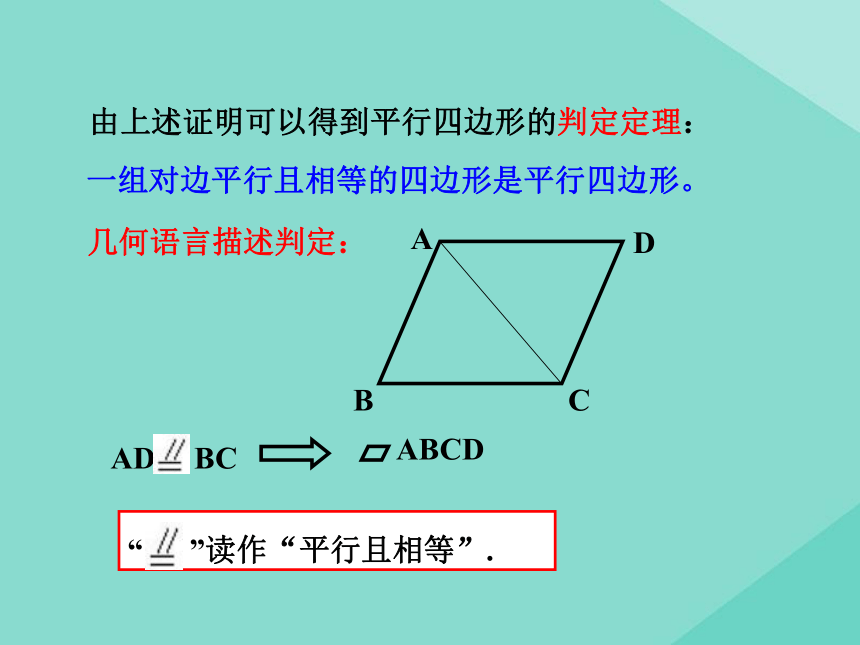
试问:四边 形ABCD是平行四边形吗?请说明理由。B解:如图,连接AC.ACD12是平行四边形。理由如下:∵AB∥CD,∴ ∠BAC=∠ACD.在△ABC和△CDA中,AB=CD (已知),∠BAC=∠ACD (已证),AC=CA (公共边),∴△ABC≌△CDA (SAS).∴ ∠1=∠2,∴ AD∥ BC.又∵ AB∥ CD,∴四边形ABCD是平行四边形.由上述证明可以得到平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形。几何语言描述判定:探究3已知:四边形ABCD中,OA=OC,OB=OD,试问:四边 形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:在△ABO和△CDO中,AO=CO(已知),∠AOB=∠COD (对顶角相等),BO=DO(已知),∴△ABO≌△CDO (SAS),∴ ∠ABO=∠ODC, ∠ BAO=∠OCD,∴AB∥ CD , AD∥ BC.∴四边形ABCD是平行四边形.对角线互相平分的四边形是平行四边形。几何语言描述判定:AO=CO
BO=DO由上述证明可以得到平行四边形的判定定理:探究4已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:∵∠A+∠C+∠B+∠D=3600,∴2∠A+2∠B=3600,即∠A+∠B=1800,∴ AD∥ BC.同理,得 AB∥ CD,∴四边形ABCD是平行四边形.∠A=∠C,∠B=∠D,由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形。几何语言描述判定:∠A=∠C
∠B=∠D三、应用练习1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的 是( )A.1:2:3:4 C.2:3:2:3 B.2:2:3:3需要两组对角分别相等.D.2:3:3:2
C 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C3、填空题: 如图,在四边形ABCD中,①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0,则四边形ABCD是平行四边形。③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。84点评:两组对边分别相等的四边形是平行四边形6012060点评:两组对角分别相等的四边形是平行四边形6点评:一组对边平行且相等的四边形是平行四边形4、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF。求证:四边形BFDE是平行四边形.O证明:连接BD.在平行四边形ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
判定 1 定义:两组对边分别平行的四边形是平行四边形。判定2 两组对边分别相等的四边形是平行四边形。判定3 两组对角分别相等的四边形是平行四边形。判定4 两条对角线互相平分的四边形是平行四边形。判定5 一组对边平行且相等的四边形是平行四边形。本节 课主要学习了平行四边形的判定定理:第18章 平行四边形
18.2 平行四边形的判定
第2课时1.回忆平行四边形的判定定理: 平形四边形的判定
两组对边分别平行的四边形是平行四边形边
一组对边平行且相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形角
对角线
温故知新两组对边分别相等的四边形是平行四边形 三、学以致用 为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?贴上图片 证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形. 例1 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形. 1. 已知:如图,在四边形 ABCD中,对角线AC和BD相交于点O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.练习例2、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形.O证明:连接BD.在平行四边形ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
大显身手练习2 已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形.DABCEFBE∥DF.练习3:已知:如图,在四边形ABCD中, ∠BAD=∠BCD, ∠B=∠D。求证:四边形ABCD是平行四边形. 判定一个四边形是平行四边形的方法:本课小结
数学 八年级下册 华东师大版
第18章 平行四边形
18.2 平行四边形的判定
第1课时知识点回顾定义:有两组对边分别平行的四边形叫做平行四边形.性质: 通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?创设情境,引入新课探究1:已知:如图,在四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:如图,连结AC.AB=CD (已知),AC=CA (公共边),BC=DA(已知),∴△ABC≌△CDA(SSS).在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4,∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:探究2已知:如图,四边形ABCD中,AB=CD, AB∥CD,
试问:四边 形ABCD是平行四边形吗?请说明理由。B解:如图,连接AC.ACD12是平行四边形。理由如下:∵AB∥CD,∴ ∠BAC=∠ACD.在△ABC和△CDA中,AB=CD (已知),∠BAC=∠ACD (已证),AC=CA (公共边),∴△ABC≌△CDA (SAS).∴ ∠1=∠2,∴ AD∥ BC.又∵ AB∥ CD,∴四边形ABCD是平行四边形.由上述证明可以得到平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形。几何语言描述判定:探究3已知:四边形ABCD中,OA=OC,OB=OD,试问:四边 形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:在△ABO和△CDO中,AO=CO(已知),∠AOB=∠COD (对顶角相等),BO=DO(已知),∴△ABO≌△CDO (SAS),∴ ∠ABO=∠ODC, ∠ BAO=∠OCD,∴AB∥ CD , AD∥ BC.∴四边形ABCD是平行四边形.对角线互相平分的四边形是平行四边形。几何语言描述判定:AO=CO
BO=DO由上述证明可以得到平行四边形的判定定理:探究4已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边形ABCD是平行四边形吗?请说明理由。解:是平行四边形。理由如下:∵∠A+∠C+∠B+∠D=3600,∴2∠A+2∠B=3600,即∠A+∠B=1800,∴ AD∥ BC.同理,得 AB∥ CD,∴四边形ABCD是平行四边形.∠A=∠C,∠B=∠D,由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形。几何语言描述判定:∠A=∠C
∠B=∠D三、应用练习1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的 是( )A.1:2:3:4 C.2:3:2:3 B.2:2:3:3需要两组对角分别相等.D.2:3:3:2
C 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C3、填空题: 如图,在四边形ABCD中,①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0,则四边形ABCD是平行四边形。③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。84点评:两组对边分别相等的四边形是平行四边形6012060点评:两组对角分别相等的四边形是平行四边形6点评:一组对边平行且相等的四边形是平行四边形4、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF。求证:四边形BFDE是平行四边形.O证明:连接BD.在平行四边形ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
判定 1 定义:两组对边分别平行的四边形是平行四边形。判定2 两组对边分别相等的四边形是平行四边形。判定3 两组对角分别相等的四边形是平行四边形。判定4 两条对角线互相平分的四边形是平行四边形。判定5 一组对边平行且相等的四边形是平行四边形。本节 课主要学习了平行四边形的判定定理:第18章 平行四边形
18.2 平行四边形的判定
第2课时1.回忆平行四边形的判定定理: 平形四边形的判定
两组对边分别平行的四边形是平行四边形边
一组对边平行且相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形角
对角线
温故知新两组对边分别相等的四边形是平行四边形 三、学以致用 为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?贴上图片 证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形. 例1 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形. 1. 已知:如图,在四边形 ABCD中,对角线AC和BD相交于点O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.练习例2、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形.O证明:连接BD.在平行四边形ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
大显身手练习2 已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形.DABCEFBE∥DF.练习3:已知:如图,在四边形ABCD中, ∠BAD=∠BCD, ∠B=∠D。求证:四边形ABCD是平行四边形. 判定一个四边形是平行四边形的方法:本课小结
