2020春华东师大版八下数学19.1矩形课件(2课时 36张)
文档属性
| 名称 | 2020春华东师大版八下数学19.1矩形课件(2课时 36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 723.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览






文档简介
课件36张PPT。教学课件
数学 八年级下册 华东师大版
第19章 矩形、菱形与正方形
19.1 矩 形
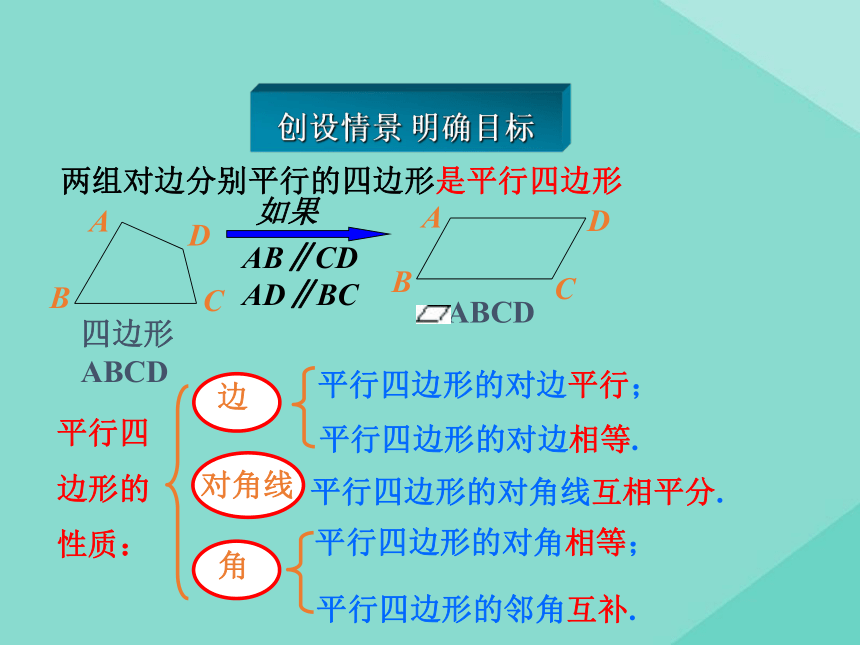
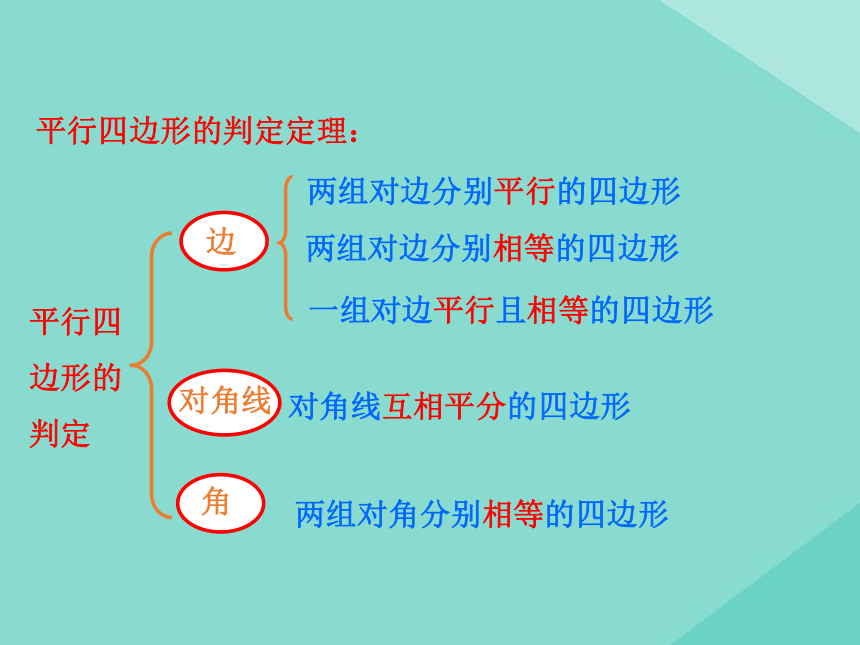
第1课时两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等.平行四边形的对角相等;平行四边形的邻角互补.平行四边形的对角线互相平分.创设情景 明确目标平行四边形的判定两组对边分别平行的四边形两组对边分别相等的四边形两组对角分别相等的四边形对角线互相平分的四边形一组对边平行且相等的四边形平行四边形的判定定理:一个角是
直角两组对边
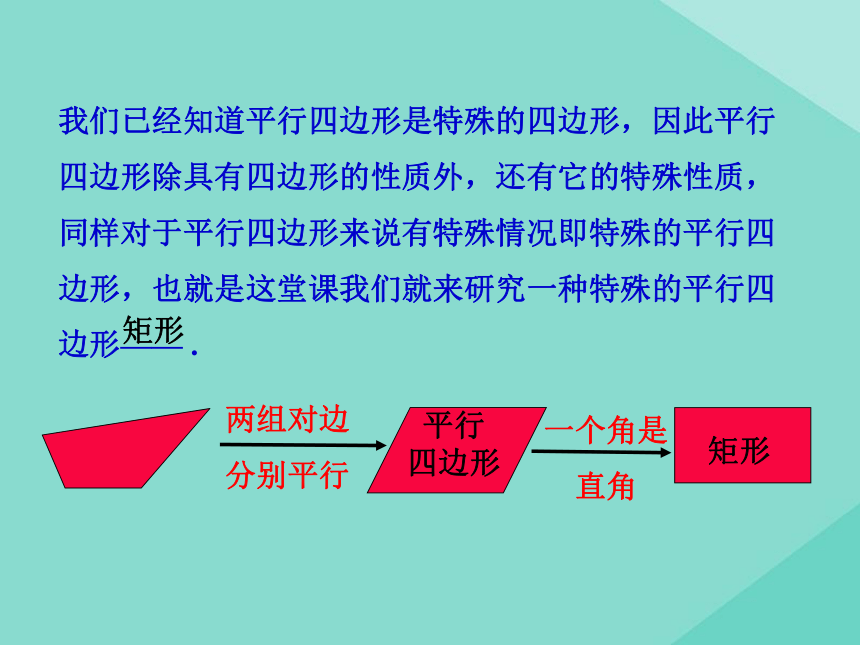
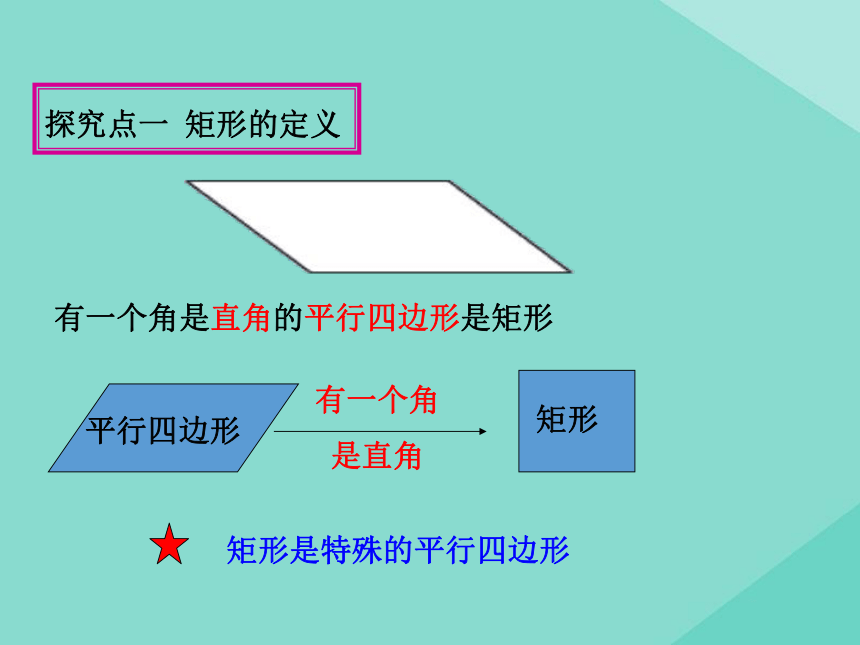
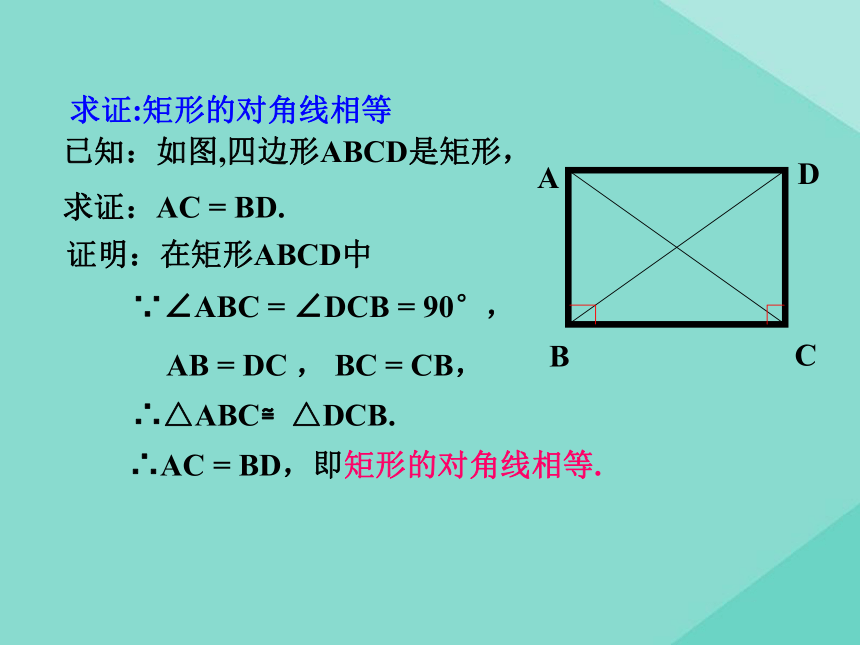
分别平行矩形我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— .矩形有一个角是直角的平行四边形是矩形探究点一 矩形的定义 对边平行且相等对角相等对角线互相平分矩形的一般性质:探究点二 矩形的性质 矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊的性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°.证明: ∵四边形ABCD是矩形,∴ ∠A=90°.又∵ 矩形ABCD是平行四边形,∴ ∠A=∠C ,∠B = ∠D
∠A +∠B = 180°.∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形,
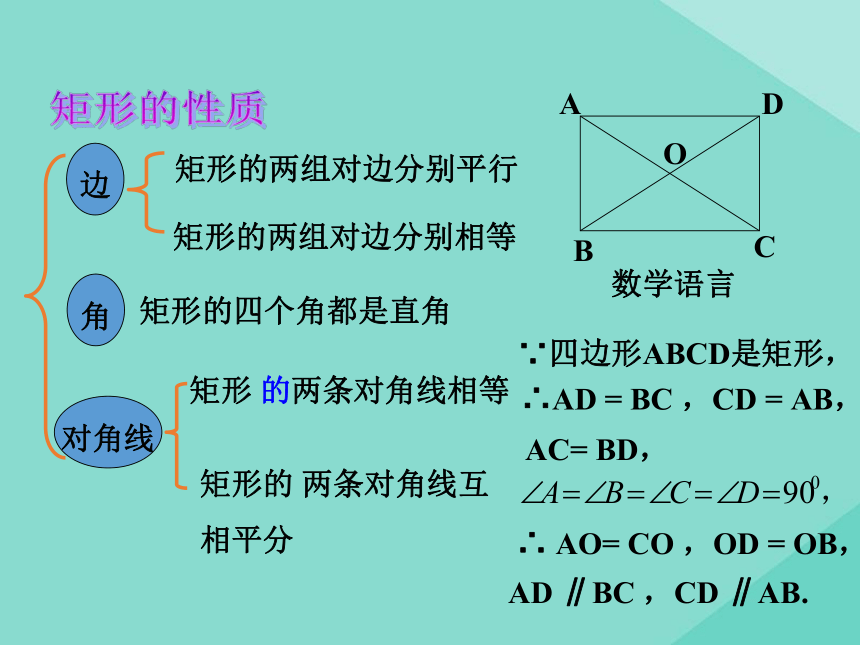
求证:AC = BD.证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°,AB = DC , BC = CB,∴△ABC≌△DCB.∴AC = BD,即矩形的对角线相等.求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的 两条对角线互
相平分矩形的两组对边分别相等 矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形,∴AD = BC ,CD = AB,AD ∥BC ,CD ∥AB.AC= BD, ∴ AO= CO ,OD = OB,矩形的性质观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴?对边平行
且相等对角相等,
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相平分且相等中心对称图
形,轴对称
图形这是矩形所特有的性质ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠OBA=∠ODC=∠OCD , ∠OAD=∠ODA=∠OBC=∠OCB.已知四边形ABCD是矩形ODCBA等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB △OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分,∴ OA=OB.∵ ∠AOB=60°,∴ △AOB是等边三角形,∴ OA=AB=4(㎝),∴ 矩形的对角线长 AC=BD=2OA=8(㎝).解:∵ 四边形ABCD是矩形,已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC.
D证明: 延长BO至点D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形. ∵∠ABC=900,∴AC=BD,探究点三 直角三角形的性质:斜边上的中线等于斜边的
一半. 直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两条对
称轴. 矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.矩形:有一个角是直角的平行四边形叫做矩形.总结梳理 内化目标1、矩形具有而一般平行四边形不具有的性质是 ( ) B.对边相等C达标检测 反思目标 已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=____㎝ , OB=____ ㎝.
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm, AB= _____cm.51043.已知△ABC是直角三角形,∠ABC=900,BD是斜边
AC上的中线.(1)若BD=3㎝ ,则AC= ㎝.
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510OABCD公平,因为OA=OC=OB=OD第19章 矩形、菱形与正方形
19.1 矩形
第2课时小明利用周末的时间,为自己做了一个相框. 问题1 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 创设情景 明确目标 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗? 1.掌握矩形的两个判定定理,能根据不同的条件,选
取适当的定理进行推理计算;
2.经历矩形判定定理的猜想与证明过程,渗透类比
思想,体会类比学习和图形判定探究的一般思路. 学习目标 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?合作探究 达成目标证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? ×√×√√练习1 现在你能帮小明解决问题了吗?小明判定相框为
矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 探究点二 矩形判定的运用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数. 在“?”号处填上恰当的条件: 总结梳理 内化目标一种学习方法
两个猜想证明
三种判定方法 1.如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分 ,
∴AO=OB=OC=OD=AB=DC=4.
∵∠AOB= ,∴∠AOD=
又∵AO=DO ,∴∠ADC= ,
∴四边形ABCD是矩形,AC=8 ,DC=4, AD= ,
∴平行四边形ABCD面积为 .达标检测 反思目标 2、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD ,OE=OA-AE,OG=OC-CG.
∵AE=CG ,∴OE=OG,
OF=OB-BF,OH=OD-DH.
∵BF=DH ,
∴OF=OH ,
∴四边形EFGH是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
EG=AC-AE-CG,
FH=BD-BF-DH,
∴EG=FH ,
∴平行四边形EFGH是矩形.
数学 八年级下册 华东师大版
第19章 矩形、菱形与正方形
19.1 矩 形
第1课时两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等.平行四边形的对角相等;平行四边形的邻角互补.平行四边形的对角线互相平分.创设情景 明确目标平行四边形的判定两组对边分别平行的四边形两组对边分别相等的四边形两组对角分别相等的四边形对角线互相平分的四边形一组对边平行且相等的四边形平行四边形的判定定理:一个角是
直角两组对边
分别平行矩形我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— .矩形有一个角是直角的平行四边形是矩形探究点一 矩形的定义 对边平行且相等对角相等对角线互相平分矩形的一般性质:探究点二 矩形的性质 矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊的性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°.证明: ∵四边形ABCD是矩形,∴ ∠A=90°.又∵ 矩形ABCD是平行四边形,∴ ∠A=∠C ,∠B = ∠D
∠A +∠B = 180°.∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形,
求证:AC = BD.证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°,AB = DC , BC = CB,∴△ABC≌△DCB.∴AC = BD,即矩形的对角线相等.求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的 两条对角线互
相平分矩形的两组对边分别相等 矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形,∴AD = BC ,CD = AB,AD ∥BC ,CD ∥AB.AC= BD, ∴ AO= CO ,OD = OB,矩形的性质观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴?对边平行
且相等对角相等,
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相平分且相等中心对称图
形,轴对称
图形这是矩形所特有的性质ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠OBA=∠ODC=∠OCD , ∠OAD=∠ODA=∠OBC=∠OCB.已知四边形ABCD是矩形ODCBA等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB △OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分,∴ OA=OB.∵ ∠AOB=60°,∴ △AOB是等边三角形,∴ OA=AB=4(㎝),∴ 矩形的对角线长 AC=BD=2OA=8(㎝).解:∵ 四边形ABCD是矩形,已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC.
D证明: 延长BO至点D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形. ∵∠ABC=900,∴AC=BD,探究点三 直角三角形的性质:斜边上的中线等于斜边的
一半. 直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两条对
称轴. 矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.矩形:有一个角是直角的平行四边形叫做矩形.总结梳理 内化目标1、矩形具有而一般平行四边形不具有的性质是 ( ) B.对边相等C达标检测 反思目标 已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=____㎝ , OB=____ ㎝.
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm, AB= _____cm.51043.已知△ABC是直角三角形,∠ABC=900,BD是斜边
AC上的中线.(1)若BD=3㎝ ,则AC= ㎝.
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510OABCD公平,因为OA=OC=OB=OD第19章 矩形、菱形与正方形
19.1 矩形
第2课时小明利用周末的时间,为自己做了一个相框. 问题1 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 创设情景 明确目标 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗? 1.掌握矩形的两个判定定理,能根据不同的条件,选
取适当的定理进行推理计算;
2.经历矩形判定定理的猜想与证明过程,渗透类比
思想,体会类比学习和图形判定探究的一般思路. 学习目标 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?合作探究 达成目标证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? ×√×√√练习1 现在你能帮小明解决问题了吗?小明判定相框为
矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( ) 探究点二 矩形判定的运用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数. 在“?”号处填上恰当的条件: 总结梳理 内化目标一种学习方法
两个猜想证明
三种判定方法 1.如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分 ,
∴AO=OB=OC=OD=AB=DC=4.
∵∠AOB= ,∴∠AOD=
又∵AO=DO ,∴∠ADC= ,
∴四边形ABCD是矩形,AC=8 ,DC=4, AD= ,
∴平行四边形ABCD面积为 .达标检测 反思目标 2、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD ,OE=OA-AE,OG=OC-CG.
∵AE=CG ,∴OE=OG,
OF=OB-BF,OH=OD-DH.
∵BF=DH ,
∴OF=OH ,
∴四边形EFGH是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
EG=AC-AE-CG,
FH=BD-BF-DH,
∴EG=FH ,
∴平行四边形EFGH是矩形.
