2020春华东师大版八下数学19.2菱形课件(2课时 41张)
文档属性
| 名称 | 2020春华东师大版八下数学19.2菱形课件(2课时 41张) |  | |
| 格式 | zip | ||
| 文件大小 | 877.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 22:40:11 | ||
图片预览






文档简介
课件41张PPT。教学课件
数学 八年级下册 华东师大版
第19章 矩形、菱形与正方形
19.2 菱形
第1课时创设情景 明确目标1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、
猜想、证明等活动,体会几何图形研究的一般步骤和
方法.
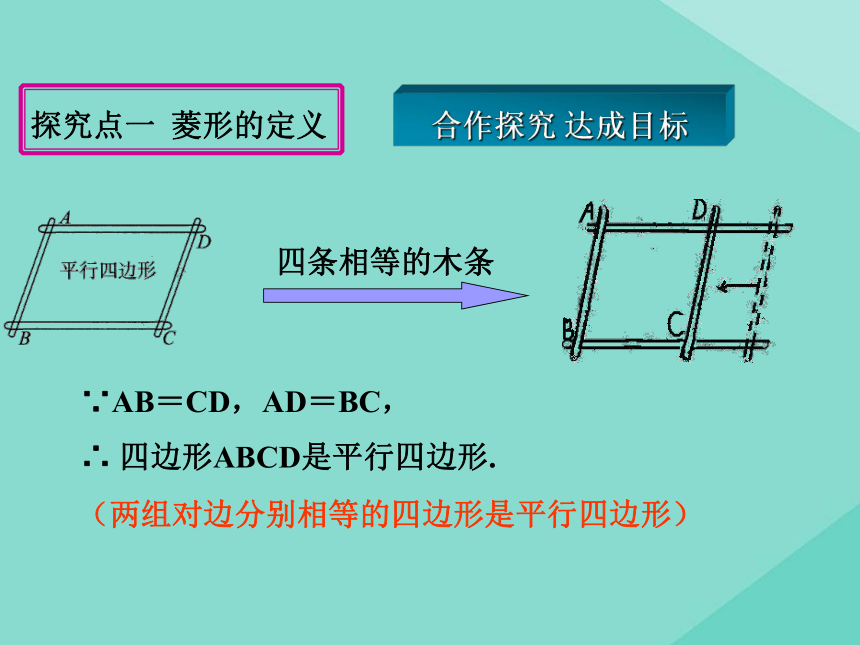
学习目标四条相等的木条 ∵AB=CD,AD=BC,
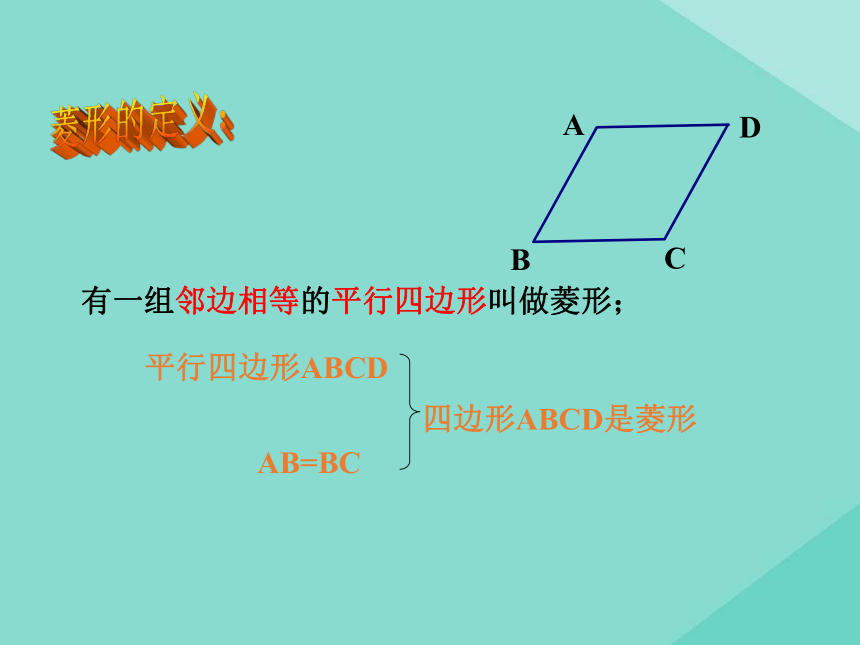
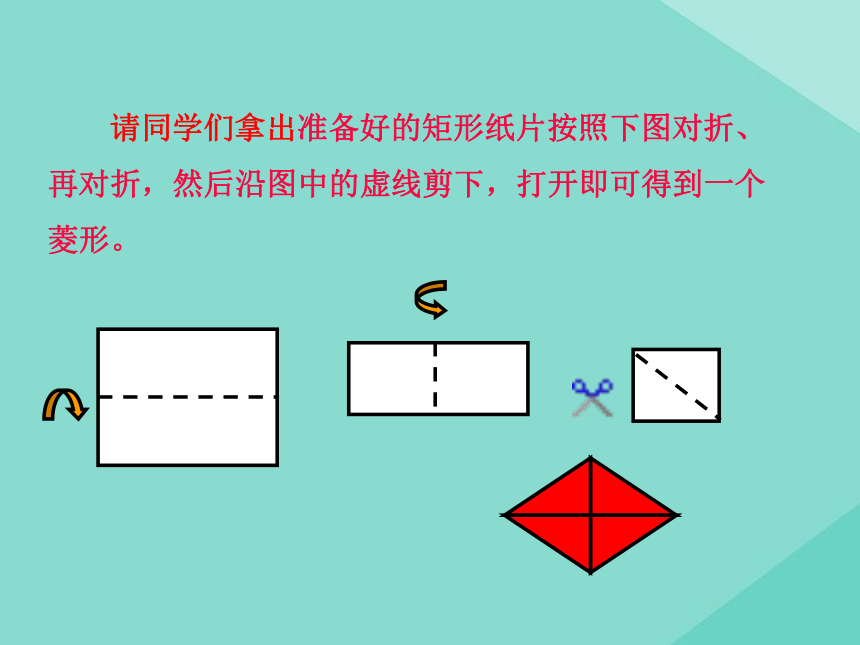
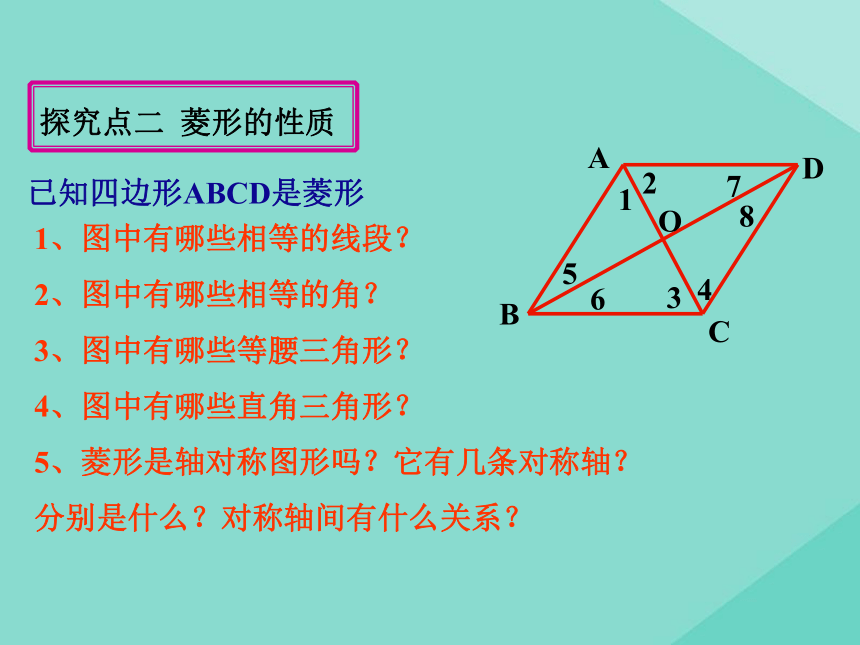
∴ 四边形ABCD是平行四边形.(两组对边分别相等的四边形是平行四边形)合作探究 达成目标探究点一 菱形的定义有一组邻边相等的平行四边形叫做菱形;菱形的定义:AB=BC四边形ABCD是菱形平行四边形ABCDA BCD 请同学们拿出准备好的矩形纸片按照下图对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形。已知四边形ABCD是菱形ABCDO123456781、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
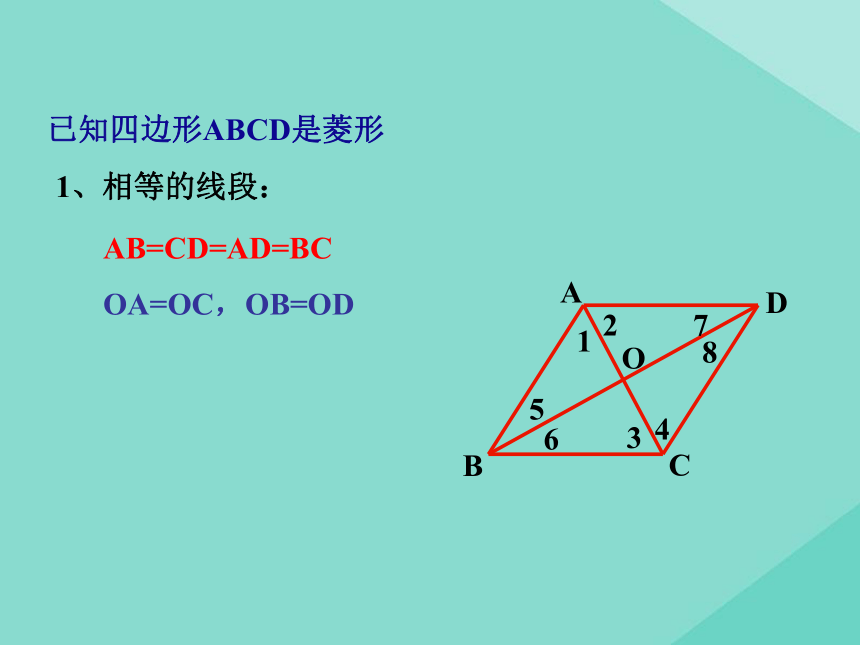
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?探究点二 菱形的性质已知四边形ABCD是菱形ABCDO123456781、相等的线段:AB=CD=AD=BC
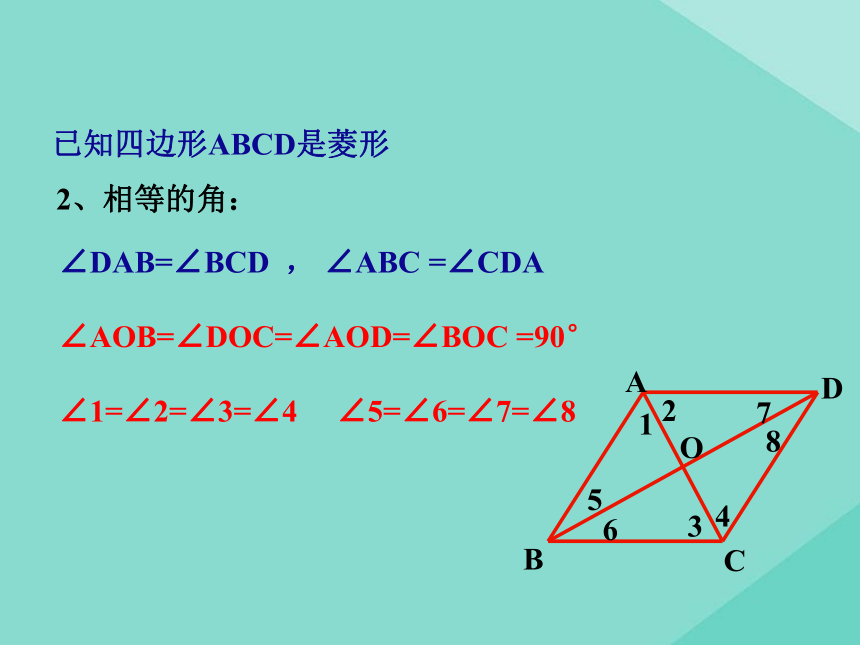
OA=OC,OB=OD已知四边形ABCD是菱形ABCDO123456782、相等的角:∠DAB=∠BCD , ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8已知四边形ABCD是菱形ABCDO123456783、等腰三角形有:△ABC △ DBC △ACD △ABD已知四边形ABCD是菱形ABCDO123456784、直角三角形有:Rt△AOB Rt△BOC Rt△COD Rt△DOA已知四边形ABCD是菱形ABCDO123456785、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系?是 两条 AC、BD所在的直线 互相垂直 命题: 菱形的四条边都相等。
ABCD命题:菱形的对角线互相垂直平分, 并且每一条对角线平分一组对角.命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形.
求证:AB=BC=CD=AD.证明:∵四边形ABCD是菱形,
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等), AB=AD (菱形的定义),
∴ AB=BC=CD=AD.ABCD已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形,在△ABD中,又∵BO=DO,∴AB=AD(菱形的四条边都相等).∴AC⊥BD,AC平分∠BAD,同理 AC平分∠BCD,
BD平分∠ABC和∠ADC.
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC. 命题:菱形的对角线互相垂直平分,并且每一条对角线平
分一组对角.【菱形的面积公式】S菱形=BC× AE想一想:已知菱形的两条对角线的长,能求出它的面积吗? 菱形的面积=底×高=对角线乘积的一半1、菱形的四条边相等2、菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。3、菱形是轴对称图形,对角线所在的直线是对称轴。E O4、菱形的面积=底×高=对角线乘积的一半菱形的性质:探究点三 菱形性质的运用如图,菱形花坛ABCD的周长为80m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2 )大显身手解:∵ 花坛ABCD是菱形,∴AC⊥BD, ∠ABO = ∠ABC = ×60°=30°, AB = BC = CD = AD = ×80 = 20 (m).在Rt△OAB中,AO= AB= ×20=10(m),BO= ≈17.32(m),∴ 花坛的两条小路长
AC = 2AO = 20 (m), BD = 2BO ≈34.64(m). 花坛的面积S菱形ABCD = AC·BD≈346.4 ( m2 ),(1)什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所
具有的?哪些是一般平行四边形不具有的?菱
形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的
体会.总结梳理 内化目标 变式 若E是BD上任意一点,那么AE与CE 有怎样
的数量关系? 1. 如图,在菱形ABCD中,若∠ABC=2∠BAD,
则∠BAD= ,△ABD为 三角形.达标检测 反思目标2、已知 四边形ABCD是菱形,O是两条对角线的交点,AB=5cm,AO=4cm,求两条对角线AC和BD 的长。3、菱形的两条对角线的长分别是6cm和8cm,求菱形的周长和面积。4、把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB第19章 矩形、菱形与正方形
19.2 菱形
第2课时 我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?创设情景 明确目标 菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件? 1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.学习目标定理1:对角线互相垂直的平行四边形是菱形. 探究点一 菱形的判定 求证:对角线互相垂直的平行四边形是菱形. 求证:四边都相等的四边形是菱形. 如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.定理2:四边都相等的四边形是菱形. 一组邻边相等的平行四边形是菱形 对角线互相垂直的平行四边形是菱形 四条边都相等的四边形是菱形 菱形证明:∵四边形ABCD是平行四边形,
∴AO= .
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点_________
______________)
∴ ABCD是菱形.(菱形的定义)⊥CO到线段两个端
点的距离相等 已知:如图,在 ABCD中,AC BD,
求证: ABCD是 .
探究点二 菱形的判定的运用 如图,AD平分∠BAC,DE∥AC交AB于点E,DF∥
AB交AC于点F.求证:四边形AEDF是菱形.三个角是直角 四条边都相等 一个角是直角 对角线相等 一组邻边相等 对角线互相垂直 两组对边分别平行 一组对边平行且相等
两组对边分别相等 两组对角分别相等
对角线互相平分 四边形 总结梳理 内化目标 1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是 .
2、菱形的两条对角线的长分别是3和4,则周长和面积分别是 , .
3、已知菱形的周长为80,其中一条对角线的长为20,则较小的角的度数为____ ,面积为_____ .
2410cm660° c㎡ c㎡ 达标检测 反思目标 4、如图,用一长一短两根木条,在它们的中点处固
定一个小钉,做成一个可转动的十字,四周围上一根橡
皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由. 5、如图,先画两条等长的线段AB,AD,然后分别
以B,D为圆心,AB长为半径画弧,两弧交点为C,连接
BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
数学 八年级下册 华东师大版
第19章 矩形、菱形与正方形
19.2 菱形
第1课时创设情景 明确目标1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、
猜想、证明等活动,体会几何图形研究的一般步骤和
方法.
学习目标四条相等的木条 ∵AB=CD,AD=BC,
∴ 四边形ABCD是平行四边形.(两组对边分别相等的四边形是平行四边形)合作探究 达成目标探究点一 菱形的定义有一组邻边相等的平行四边形叫做菱形;菱形的定义:AB=BC四边形ABCD是菱形平行四边形ABCDA BCD 请同学们拿出准备好的矩形纸片按照下图对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形。已知四边形ABCD是菱形ABCDO123456781、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?探究点二 菱形的性质已知四边形ABCD是菱形ABCDO123456781、相等的线段:AB=CD=AD=BC
OA=OC,OB=OD已知四边形ABCD是菱形ABCDO123456782、相等的角:∠DAB=∠BCD , ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8已知四边形ABCD是菱形ABCDO123456783、等腰三角形有:△ABC △ DBC △ACD △ABD已知四边形ABCD是菱形ABCDO123456784、直角三角形有:Rt△AOB Rt△BOC Rt△COD Rt△DOA已知四边形ABCD是菱形ABCDO123456785、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系?是 两条 AC、BD所在的直线 互相垂直 命题: 菱形的四条边都相等。
ABCD命题:菱形的对角线互相垂直平分, 并且每一条对角线平分一组对角.命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形.
求证:AB=BC=CD=AD.证明:∵四边形ABCD是菱形,
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等), AB=AD (菱形的定义),
∴ AB=BC=CD=AD.ABCD已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形,在△ABD中,又∵BO=DO,∴AB=AD(菱形的四条边都相等).∴AC⊥BD,AC平分∠BAD,同理 AC平分∠BCD,
BD平分∠ABC和∠ADC.
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC. 命题:菱形的对角线互相垂直平分,并且每一条对角线平
分一组对角.【菱形的面积公式】S菱形=BC× AE想一想:已知菱形的两条对角线的长,能求出它的面积吗? 菱形的面积=底×高=对角线乘积的一半1、菱形的四条边相等2、菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。3、菱形是轴对称图形,对角线所在的直线是对称轴。E O4、菱形的面积=底×高=对角线乘积的一半菱形的性质:探究点三 菱形性质的运用如图,菱形花坛ABCD的周长为80m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2 )大显身手解:∵ 花坛ABCD是菱形,∴AC⊥BD, ∠ABO = ∠ABC = ×60°=30°, AB = BC = CD = AD = ×80 = 20 (m).在Rt△OAB中,AO= AB= ×20=10(m),BO= ≈17.32(m),∴ 花坛的两条小路长
AC = 2AO = 20 (m), BD = 2BO ≈34.64(m). 花坛的面积S菱形ABCD = AC·BD≈346.4 ( m2 ),(1)什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所
具有的?哪些是一般平行四边形不具有的?菱
形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的
体会.总结梳理 内化目标 变式 若E是BD上任意一点,那么AE与CE 有怎样
的数量关系? 1. 如图,在菱形ABCD中,若∠ABC=2∠BAD,
则∠BAD= ,△ABD为 三角形.达标检测 反思目标2、已知 四边形ABCD是菱形,O是两条对角线的交点,AB=5cm,AO=4cm,求两条对角线AC和BD 的长。3、菱形的两条对角线的长分别是6cm和8cm,求菱形的周长和面积。4、把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB第19章 矩形、菱形与正方形
19.2 菱形
第2课时 我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?创设情景 明确目标 菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件? 1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.学习目标定理1:对角线互相垂直的平行四边形是菱形. 探究点一 菱形的判定 求证:对角线互相垂直的平行四边形是菱形. 求证:四边都相等的四边形是菱形. 如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.定理2:四边都相等的四边形是菱形. 一组邻边相等的平行四边形是菱形 对角线互相垂直的平行四边形是菱形 四条边都相等的四边形是菱形 菱形证明:∵四边形ABCD是平行四边形,
∴AO= .
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点_________
______________)
∴ ABCD是菱形.(菱形的定义)⊥CO到线段两个端
点的距离相等 已知:如图,在 ABCD中,AC BD,
求证: ABCD是 .
探究点二 菱形的判定的运用 如图,AD平分∠BAC,DE∥AC交AB于点E,DF∥
AB交AC于点F.求证:四边形AEDF是菱形.三个角是直角 四条边都相等 一个角是直角 对角线相等 一组邻边相等 对角线互相垂直 两组对边分别平行 一组对边平行且相等
两组对边分别相等 两组对角分别相等
对角线互相平分 四边形 总结梳理 内化目标 1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是 .
2、菱形的两条对角线的长分别是3和4,则周长和面积分别是 , .
3、已知菱形的周长为80,其中一条对角线的长为20,则较小的角的度数为____ ,面积为_____ .
2410cm660° c㎡ c㎡ 达标检测 反思目标 4、如图,用一长一短两根木条,在它们的中点处固
定一个小钉,做成一个可转动的十字,四周围上一根橡
皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由. 5、如图,先画两条等长的线段AB,AD,然后分别
以B,D为圆心,AB长为半径画弧,两弧交点为C,连接
BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
