第二章 相交线与平行线单元测试卷(含答案)
文档属性
| 名称 | 第二章 相交线与平行线单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师版七年级数学下册《相交线与平行线》测试卷
一、单选题(共6题;共12分)
1.如图把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=(?? )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
2.如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是(?? )
A.?α+β=180°??????????????????????????B.?α+β=90°??????????????????????????C.?β=3α??????????????????????????D.?α﹣β=90°
3.同一平面内有三条直线,如果其中只有两条平行,那么它们( )
A.?没有交点????????????????????????B.?有一个交点????????????????????????C.?有两个交点????????????????????????D.?有三个交点
4.下列说法:
(1)在同一平面内,不相交的两条直线一定平行.
(2)在同一平面内,不相交的两条线段一定平行.
(3)相等的角是对顶角.
(4)两条直线被第三条直线所截,同位角相等.
(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
其中,正确说法的个数是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个??????????????????????????????????????D.?4个
5.下列说法:
①两条直线相交,有公共顶点而没有公共边的两个角是对顶角;
②如果两条线段没有交点,那么这两条线段所在直线也没有交点;
③邻补角的两条角平分线构成一个直角;
④直线外一点与直线上各点连接的所有线段中,垂线段最短.
其中正确的是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个??????????????????????????????????????D.?4个
6.如果一个角是50°,那么它的余角的度数是(?? )
A.?40°?????????????????????????????????????B.?50°?????????????????????????????????????C.?100°?????????????????????????????????????D.?130°
二、填空题(共5题;共5分)
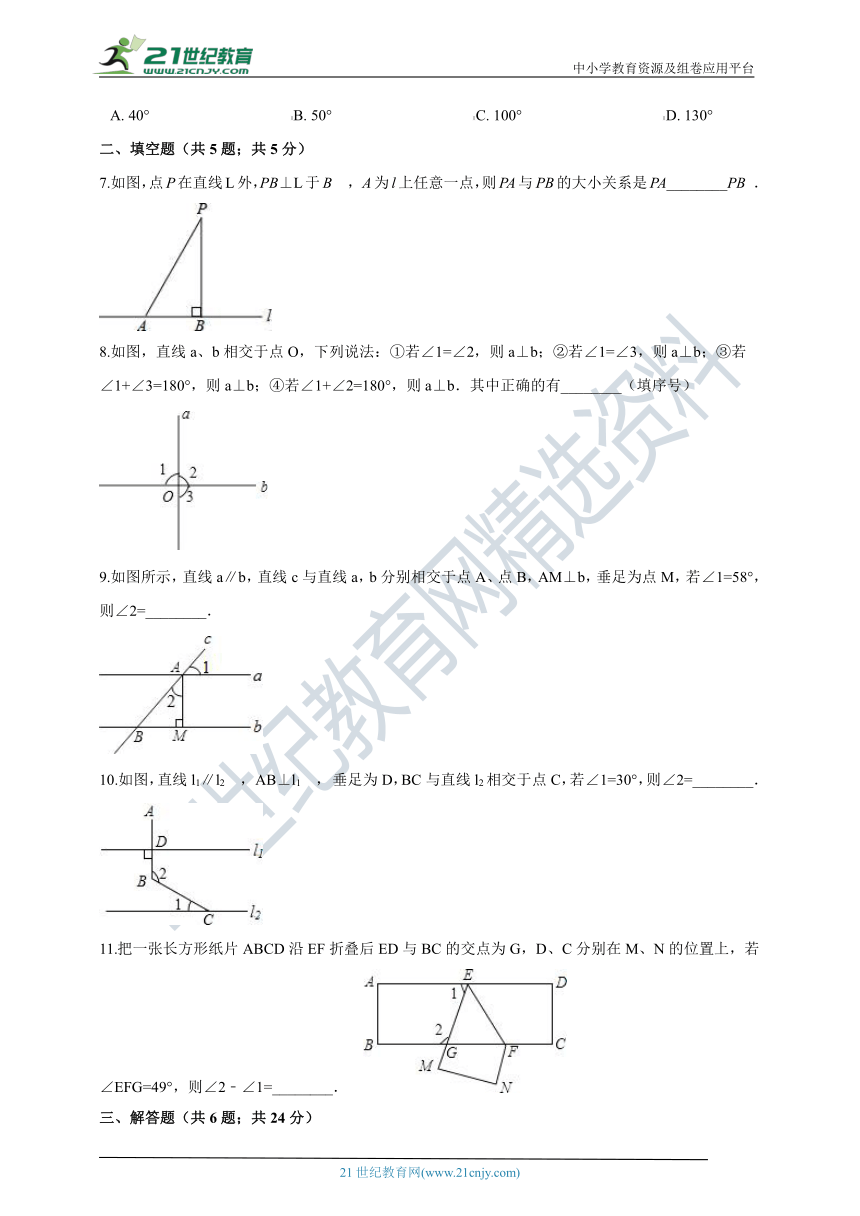
7.如图,点P在直线L外,PB⊥L于B , A为l上任意一点,则PA与PB的大小关系是PA________PB .
8.如图,直线a、b相交于点O,下列说法:①若∠1=∠2,则a⊥b;②若∠1=∠3,则a⊥b;③若∠1+∠3=180°,则a⊥b;④若∠1+∠2=180°,则a⊥b.其中正确的有________(填序号)
9.如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=58°,则∠2=________.
10.如图,直线l1∥l2 , AB⊥l1 , 垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=________.
11.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1=________.
三、解答题(共6题;共24分)
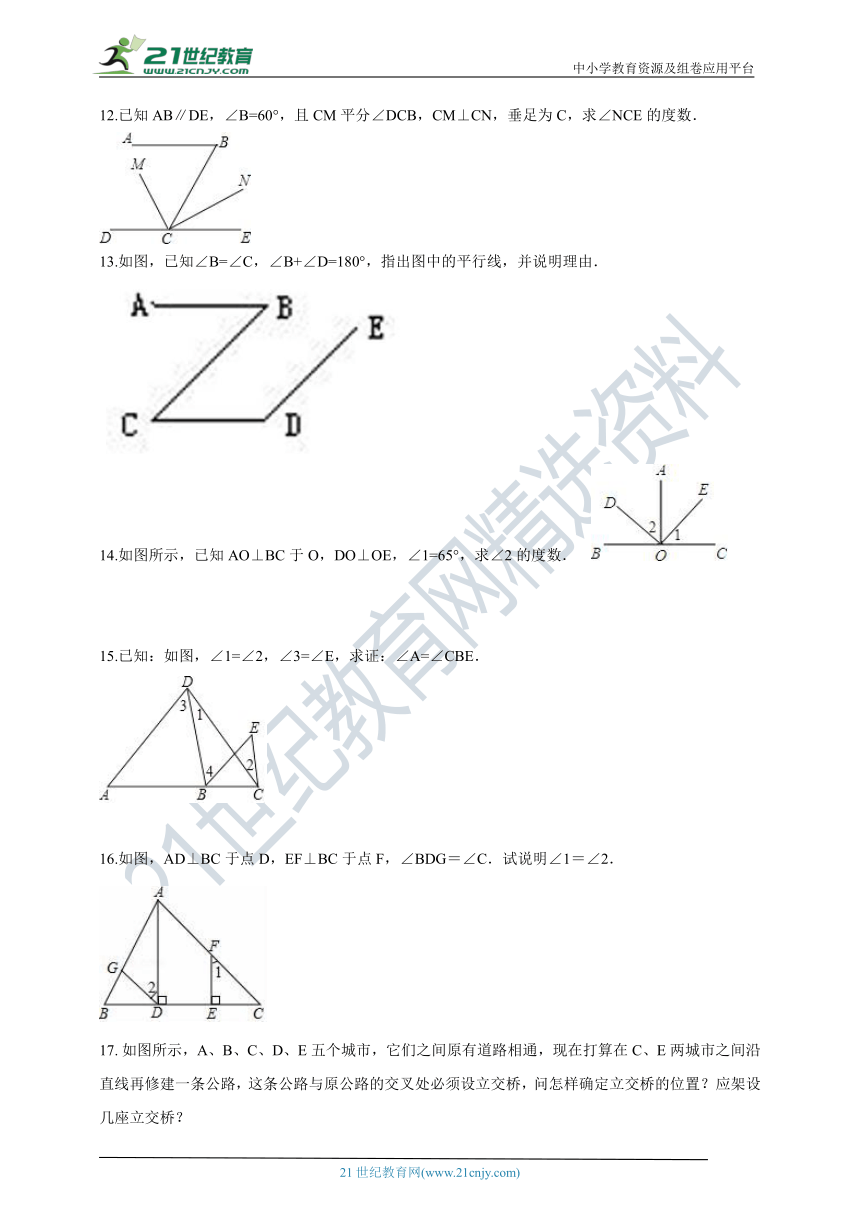
12.已知AB∥DE,∠B=60°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
13.如图,已知∠B=∠C,∠B+∠D=180°,指出图中的平行线,并说明理由.
14.如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
15.已知:如图,∠1=∠2,∠3=∠E,求证:∠A=∠CBE.
16.如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
如图所示,A、B、C、D、E五个城市,它们之间原有道路相通,现在打算在C、E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
四、作图题(共3题;共21分)
18.按要求画图:
①作 BE‖AD 交 DC 于 E .
②连接 AC ,作 BF‖AC 交 DC 的延长线于 F.
③作 AG⊥DC 于 G.
19.在△ABC中,F是BC上一点,FG⊥AB,垂足为G.
(1)过C点画CD⊥AB,垂足为D;
(2)过D点画DE//BC,交AC于E;
(3)说明∠EDC=∠GFB的理由.
20.如图,求作一点M,使MC=MD,且使M到∠AOB两边的距离相等.
五、综合题(共5题;共38分)
21.如图:
(1)如果∠1=∠4,根据________,可得AB∥CD;
(2)如果∠1=∠2,根据________,可得AB∥CD;
(3)如果∠1+∠3=180?,根据________,可得AB∥CD .
22.如图,在三角形 ABC 中, D 是 BA 延长线上一点, E 是 CA 延长线上一点, , ,
(1)DE 和 BC 平行吗?为什么?
(2) 是多少度?为什么?
23.如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
24.如图所示,BF、DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出ED、BC被BF所截的同位角,内错角,同旁内角;
(2)指出ED、BC被AC所截的内错角,同旁内角;
(3)指出FB、BC被AC所截的内错角,同旁内角.
25.如图:已知∠1=∠2,∠C=∠D,
求证:
(1)∠ABD=∠D;
(2)∠A=∠F.
答案解析部分
一、单选题
1.【答案】 C 2.【答案】 D 3.【答案】 C 4.【答案】 B 5.【答案】 C 6.【答案】A
二、填空题
7.【答案】 ≥ 8.【答案】①③ 9.【答案】32° 10.【答案】120° 11.【答案】16°
三、解答题
12.【答案】解:∵AB∥DE,∠B=60°,
∴∠BCD=120°.
∵CM平分∠DCB,
∴∠DCM= ?∠DCB=60°.
∵CM⊥CN,
∴∠MCN=90°,
∴∠DCM+∠NCE=90°,
∴∠NCE=90°﹣60°=30°.
13.【答案】 解:AB∥CD,BC∥DE
理由:∵ ∠B=∠C,
∴AB∥CD,
∵∠B+∠D=180°?,
∴ ∠C+∠D=180°?,
∴BC∥DE.
14.【答案】解:∵AO⊥BC于O, ∴∠AOC=90°,
又∠1=65°,
∴∠AOE=90°﹣65°=25°.
∵DO⊥OE,
∴∠DOE=90°,
∴∠2=∠DOE﹣∠AOE=90°﹣25°=65°
15.【答案】证明:∵∠1=∠2,
∴BD∥CE,
∴∠4=∠E,
∵∠3=∠E,
∴∠4=∠3,
∴AD∥BE,
∴∠A=∠CBE.
16.【答案】 证明:∵AD⊥BC于点D,EF⊥BC于点F,∴∠ADB=∠FEC=90°.
∵∠BDG=∠C,∠2+∠BDG=90°,∠1+∠C=90°,∴∠1=∠2.
17.【答案】解:连接CE,与BD的交点处架立交桥;1座.
四、作图题
18.【答案】解: 如图所示:BE,BF,AG即为所求;
19.【答案】(1)
(2)
(3)解:因为DE//BC,
所以∠EDC=∠BCD,
因为FG⊥AB,CD⊥AB,
所以CD//FG,
所以∠BCD=∠GFB,
所以∠EDC=∠GFB。
20.【答案】
五、综合题
21.【答案】(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)同旁内角互补,两直线平行
22.【答案】(1)解:判断:DE∥BC
理由:∵∠D=∠B=31°
∴DE∥BC
(2)解:∠C=69°,
理由:∵DE∥BC,∠E=69°
∴∠C=∠E=69°
23.【答案】(1)解:平行.理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义),
∴∠1=∠CDB,
∴AE∥FC( 同位角相等两直线平行)
(2)解:平行.理由如下:
∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行)
(3)解:平分.理由如下:
∵DA平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,AD∥BC,
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD,
∴∠EBC=∠CBD,
∴BC平分∠DBE.
24.【答案】(1)解:同位角:∠FAE和∠B;
内错角:∠B和∠DAB;
同旁内角:∠EAB和∠B
(2)解:内错角:∠EAC和∠BCA,∠DAC和∠ACG;
同旁内角:∠EAC和∠ACG,∠DAC和∠BCA
(3)解:内错角:∠BAC和∠ACG,∠FAC和∠BCA;
同旁内角:∠BAC和∠BCA,∠BAC和∠ABC,∠B和∠ACB,∠FAC和∠ACG
25.【答案】(1)证明:∵∠1=∠2,∠1=∠DMF, ∴∠DMF=∠2,
∴DB∥EC,
∴∠C=∠DBA,
∵∠D=∠C,
∴∠D=∠DBA
(2)证明:∵∠ABD=∠D, ∴DF∥AC,
∴∠A=∠F
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
