苏科版数学八下第9章《中心对称图形—平行四边形》单元检测题(解析版)
文档属性
| 名称 | 苏科版数学八下第9章《中心对称图形—平行四边形》单元检测题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 382.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览

文档简介
苏科新版八下第9章《中心对称图形—平行四边形》单元检测题
满分120分,时间100分钟
班级___________姓名____________成绩__________
一.选择题(共12小题,共36分)
1.下列图形中:①等边三角形;②矩形;③平行四边形;④菱形;既是中心对称图形又是轴对称图形的有( )个.
A.4 B.3 C.2 D.1
2.下列事件中,属于旋转运动的是( )
A.小明向北走了4米 B.时针转动
C.电梯从1楼到12楼 D.一物体从高空坠下
3.下列正多边形中,绕其中心旋转72°后,能和自身重合的是( )
A.正方形 B.正五边形 C.正六边形 D.正八边形
4.如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2 B.3 C.4 D.5
5.若平行四边形其中两个内角的度数之比为1:4,则其中较小的内角是( )
A.30° B.36° C.45° D.60°
6.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是( )
A.6 B.5 C.4 D.3
7.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
8.下列说法不正确的是( )
A.有两组对边分别平行的四边形是平行四边形 B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等 D.平行四边形的对边平行且相等
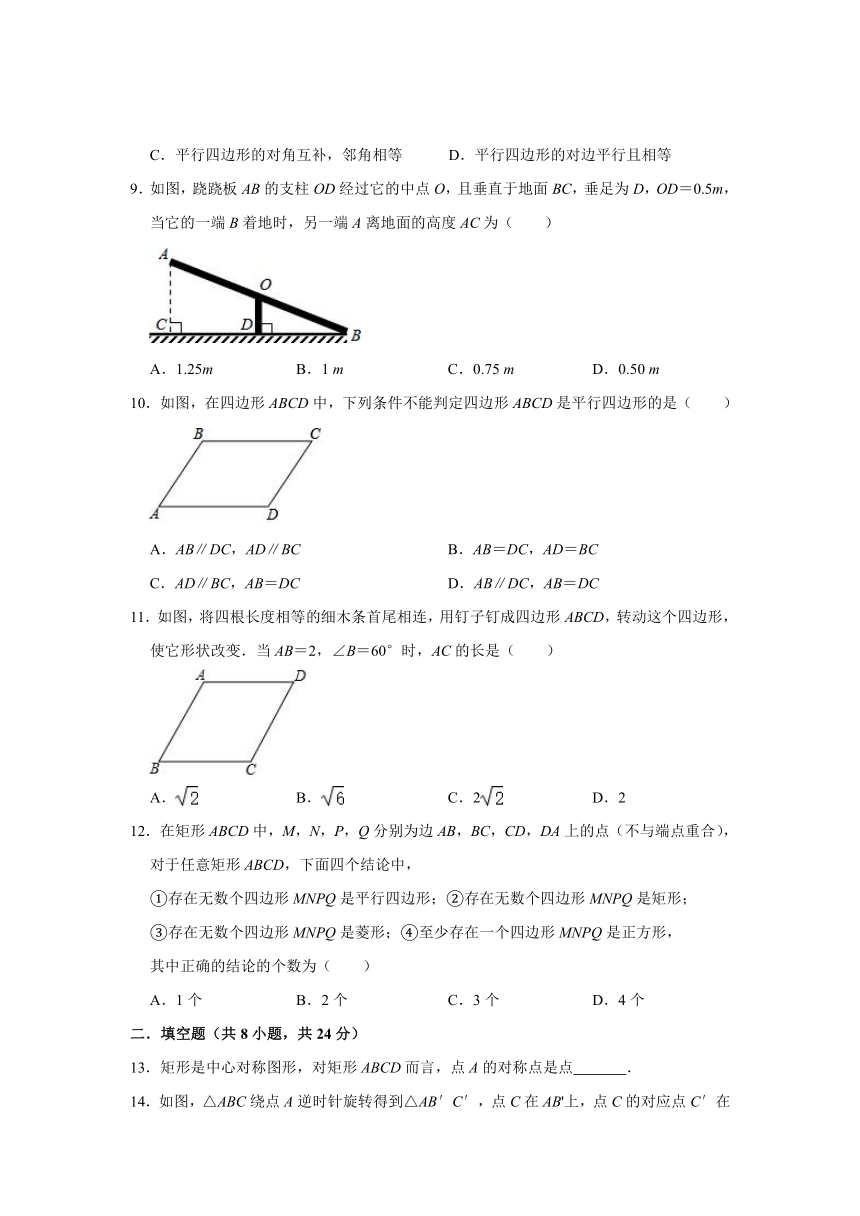
9.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.5m,当它的一端B着地时,另一端A离地面的高度AC为( )
A.1.25m B.1 m C.0.75 m D.0.50 m
10.如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AD∥BC,AB=DC D.AB∥DC,AB=DC
11.如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当AB=2,∠B=60°时,AC的长是( )
A. B. C.2 D.2
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,共24分)
13.矩形是中心对称图形,对矩形ABCD而言,点A的对称点是点 .
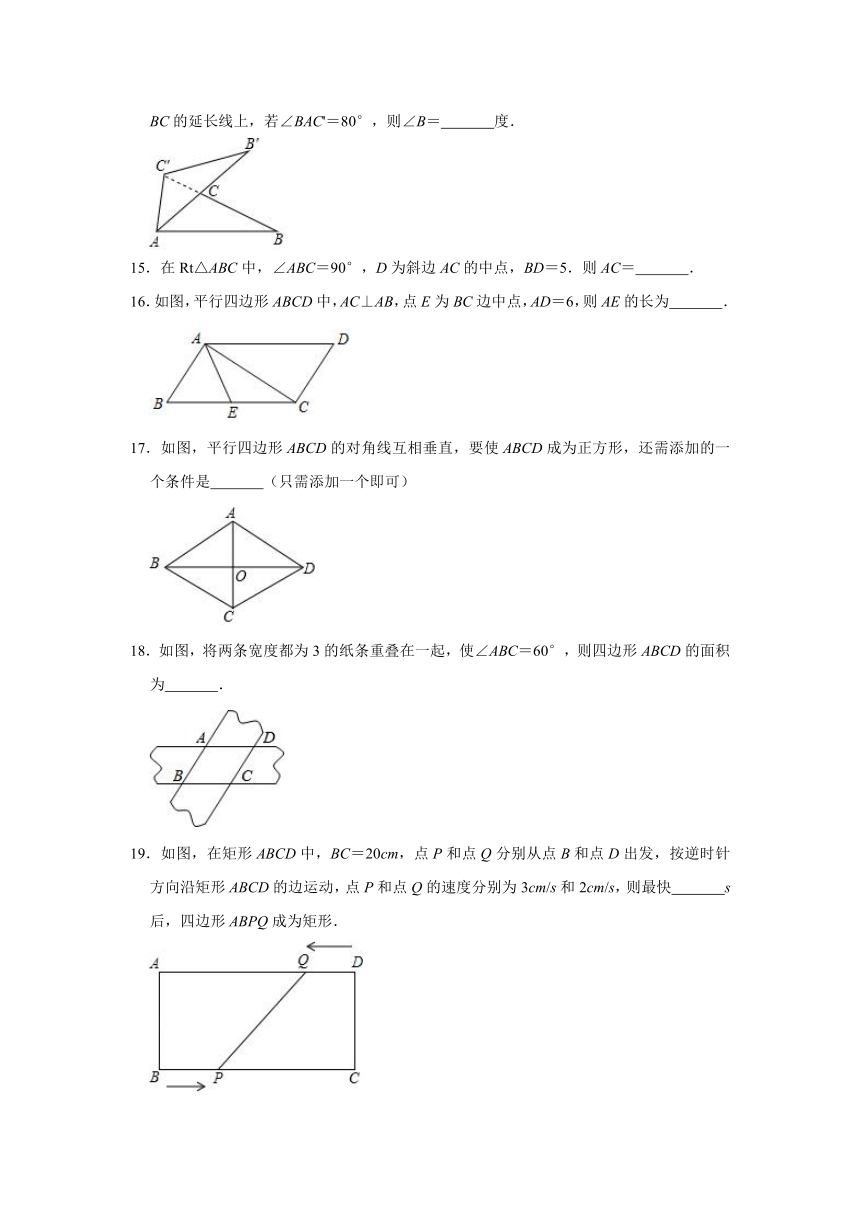
14.如图,△ABC绕点A逆时针旋转得到△AB′C′,点C在AB'上,点C的对应点C′在BC的延长线上,若∠BAC'=80°,则∠B= 度.
15.在Rt△ABC中,∠ABC=90°,D为斜边AC的中点,BD=5.则AC= .
16.如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为 .
17.如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是 (只需添加一个即可)
18.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
19.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
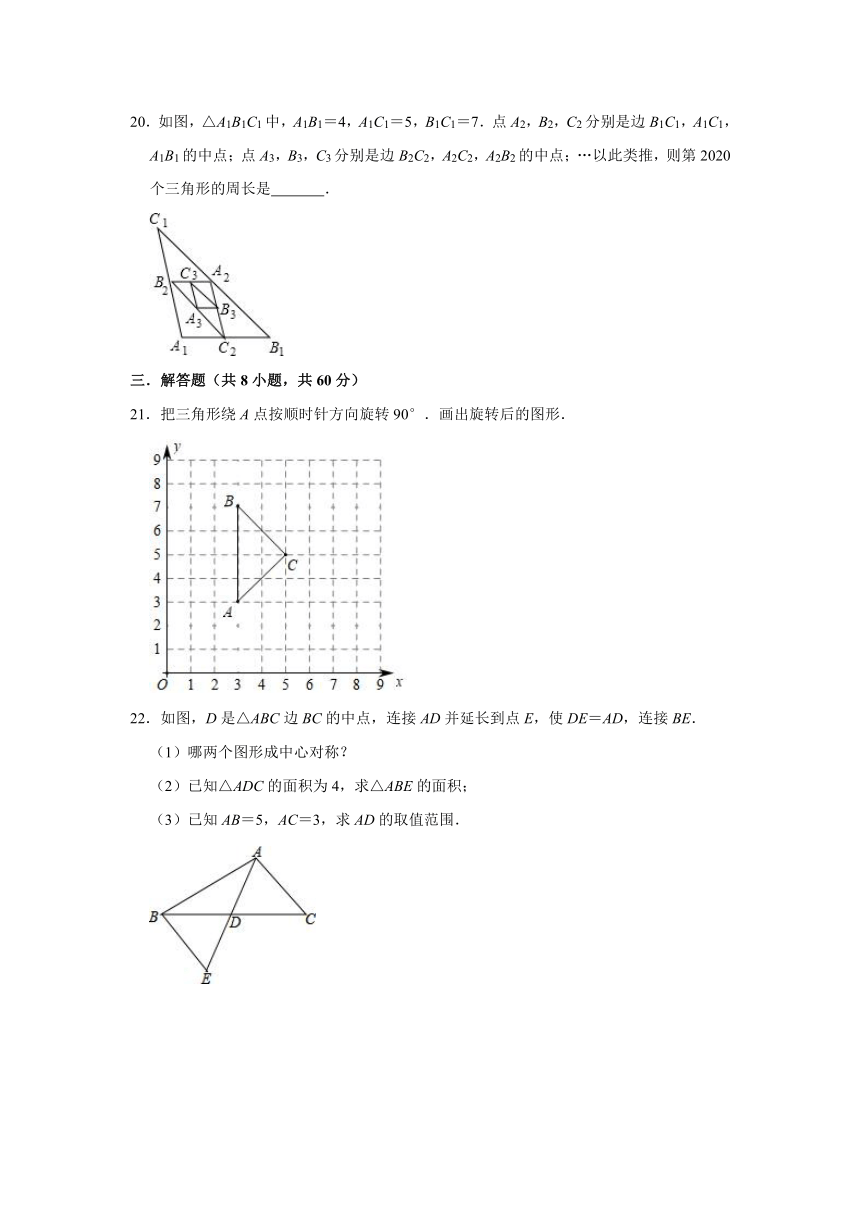
20.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第2020个三角形的周长是 .
三.解答题(共8小题,共60分)
21.把三角形绕A点按顺时针方向旋转90°.画出旋转后的图形.
22.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
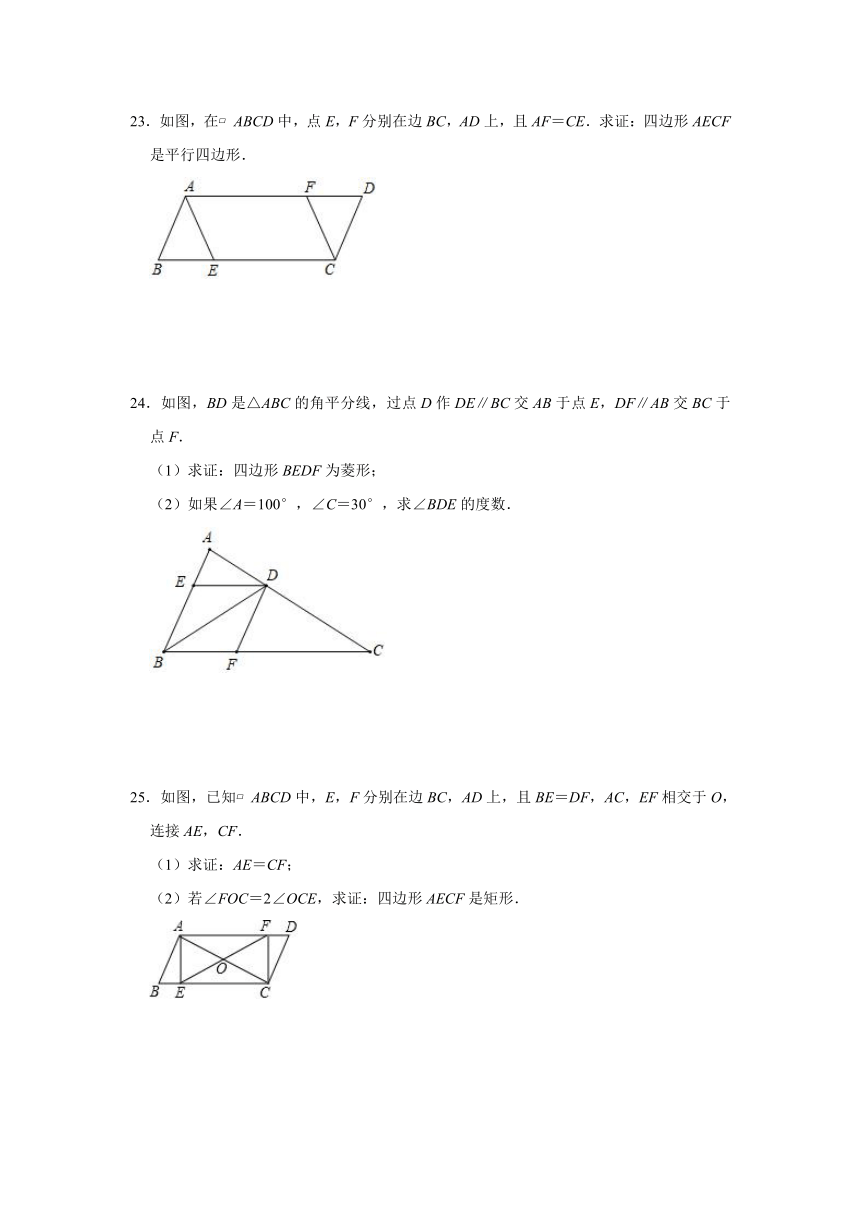
23.如图,在?ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
24.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
25.如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
(1)求证:AE=CF;
(2)若∠FOC=2∠OCE,求证:四边形AECF是矩形.
26.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE,连接BG、DE.
求证:(1)BG=DE;(2)BG⊥DE.
27.在矩形ABCD中,点E在BC上.DF⊥AE,重足为F,DF=AB.
(1)求证.AE=BC;
(2)若∠FDC=30°,且AB=4,连结DE,求∠DEF的大小和AD.
28.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连结CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
参考答案
一.选择题(共12小题)
1.下列图形中:①等边三角形;②矩形;③平行四边形;④菱形;既是中心对称图形又是轴对称图形的有( )个.
A.4 B.3 C.2 D.1
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:②矩形;④菱形既是中心对称图形又是轴对称图形,共2个,
故选:C.
2.下列事件中,属于旋转运动的是( )
A.小明向北走了4米 B.时针转动
C.电梯从1楼到12楼 D.一物体从高空坠下
【分析】把一个图形绕着某一个点旋转一个角度的图形变换叫做旋转,根据旋转的定义对各个选项进行判断即可.
【解答】解:A.小明向北走了4米是平移,不合题意;
B.时针转动是旋转运动,符合题意;
C.电梯从1楼到12楼是平移,不合题意;
D.一物体从高空坠下是平移,不合题意;
故选:B.
3.下列正多边形中,绕其中心旋转72°后,能和自身重合的是( )
A.正方形 B.正五边形 C.正六边形 D.正八边形
【分析】求出各个选项图形的最小旋转角度,即可做出判断.
【解答】解:A、正方形的最小旋转角度为90°,故本选项错误;
B、正五边形的最小旋转角度为=72°,故本选项正确;
C、正六边形的最小旋转角度为=60°,故本选项错误;
D、正八边形的最小旋转角度为=45°,故本选项错误;
故选:B.
4.如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2 B.3 C.4 D.5
【分析】由四边形ABCD为平行四边形,得到AD与BC平行,AD=BC,利用两直线平行得到一对内错角相等,由BE为角平分线得到一对角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE=4,由AD﹣AE求出ED的长即可.
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=7,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE=4,
∴ED=AD﹣AE=BC﹣AE=7﹣4=3.
故选:B.
5.若平行四边形其中两个内角的度数之比为1:4,则其中较小的内角是( )
A.30° B.36° C.45° D.60°
【分析】根据平行四边形的性质即可求解.
【解答】解:设平行四边形的一个内角为x°,则另一个内角为(4x)°,
根据平行四边形对边平行,同旁内角互补,得
x°+(4x)°=180°,解得x=36.
故选:B.
6.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是( )
A.6 B.5 C.4 D.3
【分析】直接利用三角形中位线定理与性质进而得出答案.
【解答】解:∵在△ABC中,D,E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∵DE=2,
∴BC的长度是:4.
故选:C.
7.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
【分析】根据平行四边形的性质中,两条对角线的一半和一边构成三角形,利用三角形三边关系判断可知.
【解答】解:A、对角线一半分别是2和3,2+3=5,故不能构成三角形,故本选项错误;
B、对角线一半分别是1和6,6﹣1=5,故不能构成三角形,故本选项错误.
C、对角线一半分别是2和4,符合三角形的三边关系,能构成三角形,故本选项正确;
D、对角线一半分别是2和,2+<5,故不能构成三角形,故本选项错误.
故选:C.
8.下列说法不正确的是( )
A.有两组对边分别平行的四边形是平行四边形 B.平行四边形的对角线互相平分C.平行四边形的对角互补,邻角相等 D.平行四边形的对边平行且相等
【分析】根据平行四边形的判断方法和各种性质解答即可.
【解答】解:A、平行四边形的判定定理:有两组对边分别平行的四边形是平行四边形,故本选项正确;
B、平行四边形的性质:平行四边形的对角线互相平分,故本选项正确;
C、平行四边形的对角相等,邻角互补,故本选项错误;
D、平行四边形的性质:平行四边形的对边平行且相等,故本选项正确;
故选:C.
9.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.5m,当它的一端B着地时,另一端A离地面的高度AC为( )
A.1.25m B.1 m C.0.75 m D.0.50 m
【分析】判断出OD是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AC=2OD.
【解答】解:∵O是AB的中点,OD垂直于地面,AC垂直于地面,
∴OD是△ABC的中位线,
∴AC=2OD=2×0.5=1(m).
故选:B.
10.如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AD∥BC,AB=DC D.AB∥DC,AB=DC
【分析】注意题目所问是“不能”,根据平行四边形的判定条件可解出此题.
【解答】解:平行四边形的判定条件:
1、两组对边分别平行的四边形是平行四边形(定义判定法);即选项A;
2、一组对边平行且相等的四边形是平行四边形;即选项D;
3、两组对边分别相等的四边形是平行四边形;即选项B
故选:C.
11.如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当AB=2,∠B=60°时,AC的长是( )
A. B. C.2 D.2
【分析】由题意可证△ABC是等边三角形,即可求解.
【解答】解:如图,连接AC,
∵BC=AB=2,∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
故选:D.
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理即可得到结论.
【解答】解:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,
过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,
则四边形MNPQ是平行四边形,
故存在无数个四边形MNPQ是平行四边形;故正确;
②如图,当PM=QN时,四边形MNPQ是矩形,故存在无数个四边形MNPQ是矩形;故正确;
③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;
④当四边形MNPQ是正方形时,MQ=PQ,
则△AMQ≌△DQP,
∴AM=QD,AQ=PD,
∵PD=BM,
∴AB=AD,
∴四边形ABCD是正方形,
当四边形ABCD为正方形时,四边形MNPQ是正方形,故错误;
故选:C.
二.填空题(共8小题)
13.矩形是中心对称图形,对矩形ABCD而言,点A的对称点是点 C .
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.
【解答】解:矩形是中心对称图形,对称中心是对角线的交点,点A的对称点是点C,
故答案为:C.
14.如图,△ABC绕点A逆时针旋转得到△AB′C′,点C在AB'上,点C的对应点C′在BC的延长线上,若∠BAC'=80°,则∠B= 30 度.
【分析】根据旋转的性质和等腰三角形的性质即可得到结论.
【解答】解:∵△ABC绕点A逆时针旋转得到△AB′C′,
∴∠C′AB′=∠CAB,AC′=AC,
∵∠BAC'=80°,
∴∠C′AB′=∠CAB=C′AB=40°,
∴∠ACC′=70°,
∴∠B=∠ACC′﹣∠CAB=30°,
故答案为:30.
15.在Rt△ABC中,∠ABC=90°,D为斜边AC的中点,BD=5.则AC= 10 .
【分析】根据直角三角形斜边上的中线性质得出AC=2BD,代入求出即可.
【解答】解:∵在Rt△ABC中,∠ABC=90°,D为斜边AC的中点,BD=5,
∴AC=2BD=2×5=10,
故答案为:10.
16.如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为 3 .
【分析】AC⊥AB,点E为BC边中点,所以AE=BE=EC
【解答】解:∵AC⊥AB,点E为BC边中点,
∴AE=BE=EC
∵四边形ABCD为平行四边形ABCD
∴AD=BC=6
∴AE=3
故答案为3.
17.如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是 ∠ABC=90°或AC=BD (只需添加一个即可)
【分析】此题是一道开放型的题目,答案不唯一,添加一个条件符合正方形的判定即可.
【解答】解:条件为∠ABC=90°或AC=BD,
理由是:∵平行四边形ABCD的对角线互相垂直,
∴四边形ABCD是菱形,
∵∠ABC=90°或AC=BD,
∴四边形ABCD是正方形,
故答案为:∠ABC=90°或AC=BD.
18.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 6 .
【分析】先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
【解答】解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°﹣60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=AB2+32,
解得AB=2,
∴S四边形ABCD=BC?AE=2×3=6.
故答案是:6.
19.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 4 s后,四边形ABPQ成为矩形.
【分析】根据矩形的性质,可得BC与AD的关系,根据矩形的判定定理,可得BP=AQ,构建一元一次方程,可得答案.
【解答】解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
20.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第2020个三角形的周长是 .
【分析】由三角形的中位线定理得:B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求出结论.
【解答】解:∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,
∴△A1B1C1的周长是16,
∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,
∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,
…,
以此类推,则△A4B4C4的周长是×16,
∴△AnBn?n的周长是,
则第2020个三角形的周长是=.
故答案为:.
三.解答题(共8小题)
21.把三角形绕A点按顺时针方向旋转90°.画出旋转后的图形.
【分析】利用网格特点和旋转的性质画出B、C的对应点B′、C′即可.
【解答】解:如图,△AB′C′为所作.
22.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
【分析】(1)直接利用中心对称的定义写出答案即可;
(2)根据成中心对称的图形的两个图形全等确定三角形BDE的面积,根据等底同高确定ABD的面积,从而确定ABE的面积;
(3)可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,即可解题.
【解答】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△CDE中,,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE
∵△ACE中,AC﹣AB<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
23.如图,在?ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
【分析】只要证明AF=CE,AF∥CE即可;
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
24.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
【分析】(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;
(2)由三角形内角和定理求出∠ABC=50°,由菱形的性质即可得出答案.
【解答】(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=100°,∠C=30°,
∴∠ABC=180°﹣100°﹣30°=50°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=50°,∠BDE=∠EDF=25°.
25.如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
(1)求证:AE=CF;
(2)若∠FOC=2∠OCE,求证:四边形AECF是矩形.
【分析】(1)只要证明四边形AECF是平行四边形即可解决问题;
(2)只要证明AC=EF即可解决问题.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BE=DF,
∴AF=CE,AF∥EC,
∴四边形AECF是平行四边形,
∴AE=CF.
(2)∵∠FOC=∠OEC+∠OCE=2∠OCE,
∴∠OEC=∠OCE,
∴OE=OC,
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴四边形AECF是矩形.
26.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE,连接BG、DE.
求证:(1)BG=DE;(2)BG⊥DE.
【分析】先证∠BCG=∠DCE,再证明△BCG≌△DCE,即可得出结论.
【解答】证明:(1)∵四边形ABCD和CEFG为正方形,
∴BC=DC,CG=CE,∠BCD=∠GCE=90°,
∴∠BCD+∠DCG=∠GCE+∠DCG,
即:∠BCG=∠DCE,
在△BCG和△DCE中,,
∴△BCG≌△DCE(SAS),
∴BG=DE,
(2)∵△BCG≌△DCE,
∴∠GBC=∠EDC,
∵∠GBC+∠BOC=90°,∠BOC=∠DOG,
∴∠DOG+∠EDC=90°,
∴BG⊥DE.
27.在矩形ABCD中,点E在BC上.DF⊥AE,重足为F,DF=AB.
(1)求证.AE=BC;
(2)若∠FDC=30°,且AB=4,连结DE,求∠DEF的大小和AD.
【分析】(1)证明△ABE≌△DFA(AAS),得出AE=AD,进而得出结论;
(2)证明Rt△DEF≌Rt△DCE(HL),得出∠FDE=∠CDE,由直角三角形的性质进而得出答案.
【解答】(1)证明:∵四边形ABCD是矩形,
∴DA∥BC,∠B=∠ADC,
∴∠DAE=∠AEB,
∴在△ABE与△DFA中,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∵AD=BC,
∴AE=BC;
(2)解:∵DF⊥AE,∠C=90°,
∴∠DFE∥∠DCE,
∵AB=DF,且AB=DC,
∴DF=DC,
∴在Rt△DEF与Rt△DCE中,
∴Rt△DEF≌Rt△DCE(HL),
∴∠FDE=∠CDE,
∵∠FDC=30°,
∴∠FDE=∠CDE=30°÷2=15°,
∴∠DEF=180°﹣90°﹣15°=75°,
∵△ABE≌△DFA,AB=4,
∴DF=4,
∵∠FDC=30°,
∴∠ADF=90°﹣30°=60°,
∴∠DAE=180°﹣90°﹣60°=30°,
∵∠DF=4,
∴AD=4×2=8,
∴∠DEF=75°,AD=8.
28.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连结CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
【分析】(1)直接利用三角形中位线定理得出四边形DCFE是平行四边形,进而得出DE=FC;
(2)△ABC的面积=四边形BDEF的面积,由三角形中位线定理可得△ADE的面积=△ECF的面积,问题得证.
【解答】解:(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=FC,
∵DE∥FC,
∴四边形DCFE是平行四边形,
∴CD=EF;
(2)猜想:△ABC的面积=四边形BDEF的面积,理由如下:
∵DE为△ABC的中位线,
∴DE∥BC,DE=BC
∴△ADE的面积=△DEC的面积,
∴四边形DCFE是平行四边形,
∴△DEC的面积=△ECF的面积,
∴△ADE的面积=△ECF的面积,
∴△ABC的面积=四边形BDEF的面积.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
