沪教版八年级下册22.3梯形 同步练习卷 含解析
文档属性
| 名称 | 沪教版八年级下册22.3梯形 同步练习卷 含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 15:09:52 | ||
图片预览



文档简介
八年级数学(下)第22章 四边形 第3节 梯形 同步练习卷
一.选择题(共6小题)
1.小明用两根同样长的竹棒做对角线,制作四边形的风筝,则该风筝的形状一定是
A.矩形 B.正方形 C.等腰梯形 D.无法确定
2.两个全等的等腰直角三角形拼成一个四边形,则可拼成的四边形是
A.平行四边形 B.正方形或平行四边形
C.正方形或平行四边形或梯形 D.正方形
3.如图,在中,,分别是,边的中点,若,则的长度是
A.6 B.5 C.4 D.3
4.一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为
A. B. C. D.
5.如图,中,是的中点,,连结,若,则的值为
A.1 B.2 C.3 D.4
6.如图,将面积为的沿方向平移,得到,连接,测得,则梯形的面积为
A. B. C. D.
二.填空题(共12小题)
7.在中,是中位线,是中线,则当满足 时,.
8.如图,在梯形中,,,对角线,且,则梯形的中位线的长为 .
9.在中,,,,点,,分别是,,边的中点,则的周长是 .
10.梯形中,,,,那么 .
11.如图,在四边形中,,,分别是,的中点,已知,,则 .
12.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得,.已知梯形的两底,请你求出另外两个角的度数是 , ;
13.如图,在梯形中,,若,,则梯形的周长为 .
14.如果一个直角梯形的一条底边长为7厘米,两腰长分别为8厘米和10厘米,那么这个梯形的中位线是 厘米.
15.如图,在中,、分别是、的中点,点在上,是的平分线,若,则的度数是 .
16.梯形中,,,,,,是的中点,是的中点,则线段的长为 .
17.如图,在等腰梯形中,,,,,,则 .
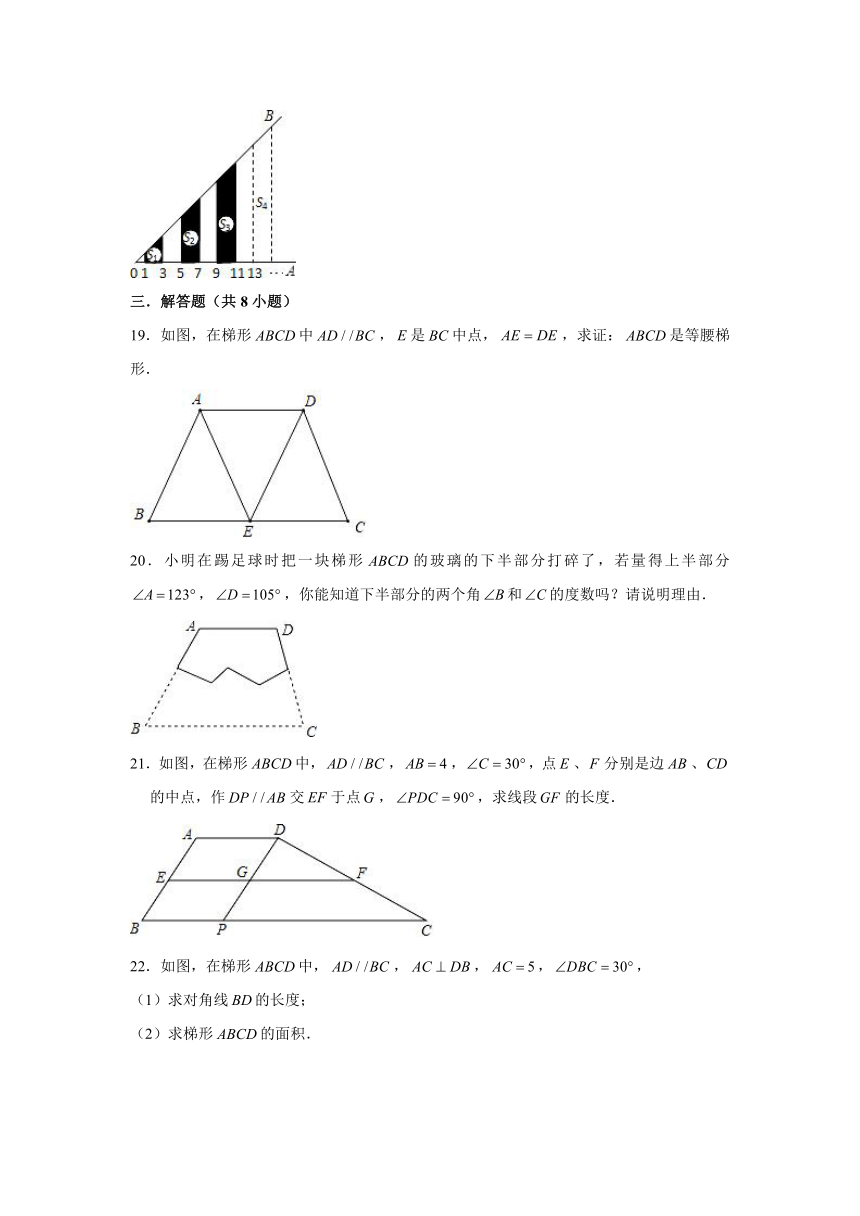
18.如图,,过上到点的距离分别为1,3,5,7,9,的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为,,,则第一个黑色梯形的面积 ;观察图中的规律,第为正整数)个黑色梯形的面积 .
三.解答题(共8小题)
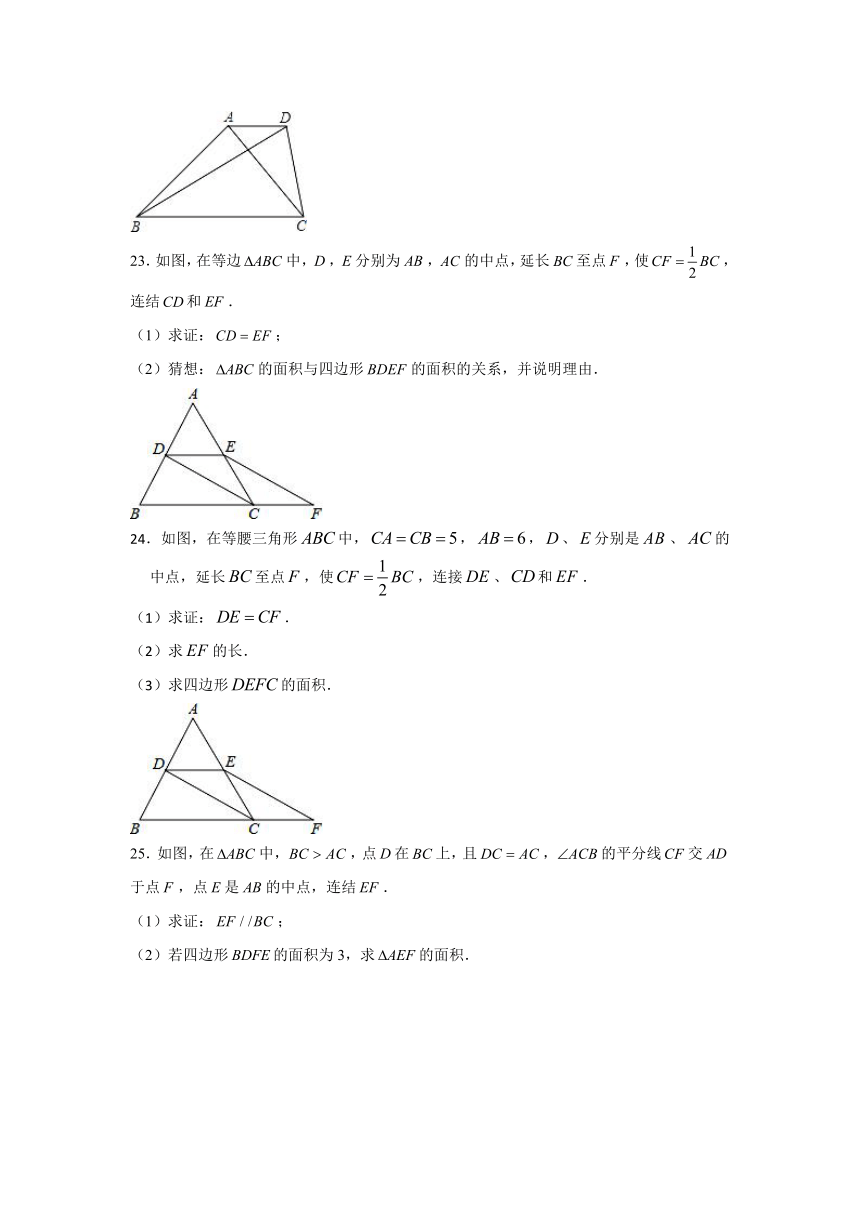
19.如图,在梯形中,是中点,,求证:是等腰梯形.
20.小明在踢足球时把一块梯形的玻璃的下半部分打碎了,若量得上半部分,,你能知道下半部分的两个角和的度数吗?请说明理由.
21.如图,在梯形中,,,,点、分别是边、的中点,作交于点,,求线段的长度.
22.如图,在梯形中,,,,,
(1)求对角线的长度;
(2)求梯形的面积.
23.如图,在等边中,,分别为,的中点,延长至点,使,连结和.
(1)求证:;
(2)猜想:的面积与四边形的面积的关系,并说明理由.
24.如图,在等腰三角形中,,,、分别是、的中点,延长至点,使,连接、和.
(1)求证:.
(2)求的长.
(3)求四边形的面积.
25.如图,在中,,点在上,且,的平分线交于点,点是的中点,连结.
(1)求证:;
(2)若四边形的面积为3,求的面积.
26.如图,在梯形中,,,,,,点从点开始,沿边向运动,速度为1厘米秒,点从点开始沿边向点运动,速度为2厘米秒,设四边形的面积为.
(1)写出面积与时间之间的函数关系式;
(2)当为何值时,四边形是平行四边形?
(3)当为何值时,四边形是等腰梯形?
参考答案
一.选择题(共6小题)
1.小明用两根同样长的竹棒做对角线,制作四边形的风筝,则该风筝的形状一定是
A.矩形 B.正方形 C.等腰梯形 D.无法确定
【解答】解:用两根同样长的竹棒做对角线,制作四边形的风筝,
则该风筝的形状可能是正方形,矩形,等腰梯形,一般的四边形等,
所以是无法确定.
故选:.
2.两个全等的等腰直角三角形拼成一个四边形,则可拼成的四边形是
A.平行四边形 B.正方形或平行四边形
C.正方形或平行四边形或梯形 D.正方形
【解答】解:如图所示,可拼成的四边形是正方形或平行四边形.
故选:.
3.如图,在中,,分别是,边的中点,若,则的长度是
A.6 B.5 C.4 D.3
【解答】解:在中,,分别是,边的中点,
是的中位线,
,
的长度是:4.
故选:.
4.一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为
A. B. C. D.
【解答】解:如图,作、,四边形为等腰梯形,,,,
四边形为等腰梯形,
,,
,,,
为矩形,
,,
,
,
,
,
,
为等腰直角三角形,
.
故选:.
5.如图,中,是的中点,,连结,若,则的值为
A.1 B.2 C.3 D.4
【解答】解:是的中点,,
.
,
,
,
故选:.
6.如图,将面积为的沿方向平移,得到,连接,测得,则梯形的面积为
A. B. C. D.
【解答】解:将面积为的沿方向平移,得到,连接,测得,
,
梯形的高的高,
梯形的面积,
故选:.
二.填空题(共12小题)
7.在中,是中位线,是中线,则当满足 直角三角形 时,.
【解答】解:连接,
是中位线,
,
,,
,
四边形为平行四边形,
,
,,
,
为直角三角形,
故答案为:直角三角形.
8.如图,在梯形中,,,对角线,且,则梯形的中位线的长为 5 .
【解答】解:过作交的延长线于,
,,
四边形是平行四边形,
,
等腰梯形中,
,,
是等腰直角三角形,
,
,
梯形的中位线,
故答案为:5.
9.在中,,,,点,,分别是,,边的中点,则的周长是 6 .
【解答】解:中,,,,
,
点、、是三边的中点,
,,,
的周长,
故答案为:6.
10.梯形中,,,,那么 .
【解答】解:如图,取的中点,连接,
,
,
,
又,
,
,
,
,
,
,
又,即,
四边形为平行四边形,
,
,
由勾股定理得:.
故答案为:.
11.如图,在四边形中,,,分别是,的中点,已知,,则 3 .
【解答】解:连接并延长交于,
,
,
在和中,
,
,,
,
,,
,
故答案为:3.
12.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得,.已知梯形的两底,请你求出另外两个角的度数是 , ;
【解答】解:在梯形中,
,
而,.
,
故答案为,.
13.如图,在梯形中,,若,,则梯形的周长为 15 .
【解答】解:过点作,交于点,
,
四边形是平行四边形,,
,,
,
是等边三角形,
,
,
梯形的周长为:.
故答案为:15.
14.如果一个直角梯形的一条底边长为7厘米,两腰长分别为8厘米和10厘米,那么这个梯形的中位线是 10或4 厘米.
【解答】解:如图,作,已知,分两种情况:
(1)当时
梯形的中位线是:
(2)当时
由(1)知:
梯形的中位线是:
故答案为:10或4.
15.如图,在中,、分别是、的中点,点在上,是的平分线,若,则的度数是 .
【解答】解:在中,、分别是、的中点,
是中位线,
,
.
又是的角平分线,
,
,
.
故答案为:.
16.梯形中,,,,,,是的中点,是的中点,则线段的长为 505 .
【解答】解:过作,,
,,
,,
.
,
,
,
,
,
,
,
,
故答案为:505.
17.如图,在等腰梯形中,,,,,,则 84 .
【解答】解:如图,连接,过点作于点,过点作于点,则,,.
在直角中,,
在直角中,,
又,,
,即.
故答案是:84.
18.如图,,过上到点的距离分别为1,3,5,7,9,的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为,,,则第一个黑色梯形的面积 4 ;观察图中的规律,第为正整数)个黑色梯形的面积 .
【解答】解:,
图形中三角形都是等腰直角三角形,
;
.
三.解答题(共8小题)
19.如图,在梯形中,是中点,,求证:是等腰梯形.
【解答】证明:,
,
,
,,
,
是中点,
,
在和中,
,
,
,
梯形是等腰梯形.
20.小明在踢足球时把一块梯形的玻璃的下半部分打碎了,若量得上半部分,,你能知道下半部分的两个角和的度数吗?请说明理由.
【解答】解:,
,,
,,
21.如图,在梯形中,,,,点、分别是边、的中点,作交于点,,求线段的长度.
【解答】解:,,
四边形是平行四边形.
点,分别是边,的中点,
,
四边形和四边形都是平行四边形,
.
,,,
,
线段的长度是4.
22.如图,在梯形中,,,,,
(1)求对角线的长度;
(2)求梯形的面积.
【解答】解:(1)如图,过作交延长线于,
,,
,,
,即为直角三角形,
,
,
且,
四边形为平行四边形.
;
(2)记梯形的面积为,过作于,则为直角三角形.
,即梯形的高,
四边形为平行四边形,
.
.
23.如图,在等边中,,分别为,的中点,延长至点,使,连结和.
(1)求证:;
(2)猜想:的面积与四边形的面积的关系,并说明理由.
【解答】解:(1)、分别为、的中点,
为的中位线,
,,
,
,
,
四边形是平行四边形,
;
(2)猜想:的面积四边形的面积,理由如下:
为的中位线,
,
的面积的面积,
四边形是平行四边形,
的面积的面积,
的面积的面积,
的面积四边形的面积.
24.如图,在等腰三角形中,,,、分别是、的中点,延长至点,使,连接、和.
(1)求证:.
(2)求的长.
(3)求四边形的面积.
【解答】(1)证明:、分别是、的中点,
是的中位线.
.
又
;
(2)解:.理由如下:
在等腰三角形中,,,点是的中点,
,,
在中,,,由勾股定理可得,
,
由(1)可知,是的中位线.
,
又,
四边形是平行四边形.
;
(3)解:四边形的面积为6,理由如下:
过点作,垂足为点.
,
,
,
.
25.如图,在中,,点在上,且,的平分线交于点,点是的中点,连结.
(1)求证:;
(2)若四边形的面积为3,求的面积.
【解答】解:(1),平行,
是的中点,
又是的中点,
是的中位线,
;
(2)是的中位线,
,,
如图,连接,则,
又四边形的面积为3,
,
又是的中点,
.
26.如图,在梯形中,,,,,,点从点开始,沿边向运动,速度为1厘米秒,点从点开始沿边向点运动,速度为2厘米秒,设四边形的面积为.
(1)写出面积与时间之间的函数关系式;
(2)当为何值时,四边形是平行四边形?
(3)当为何值时,四边形是等腰梯形?
【解答】解:(1)根据题意得:,,则,
;
面积与时间之间的函数关系式为:;
(2)点的速度为,点的速度为,
,,
四边形是平行四边形时,,
,
解得;
当时,四边形是平行四边形;
(3)如图,过点作于,
,,
四边形是矩形,
,
,
四边形是等腰梯形时,,
,
解得.
当时,四边形是等腰梯形.
