人教版物理必修二 7.5探究弹性势能的表达式(共21张PPT)
文档属性
| 名称 | 人教版物理必修二 7.5探究弹性势能的表达式(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-25 16:08:35 | ||
图片预览






文档简介
(共21张PPT)
5探究弹性势能的
表达式
高一物理
试一试:为什么松手后圆珠笔会跳起来?
有魔力的橡皮筋
想一想:橡皮筋具有魔力的秘密是什么?
三张图中的物体有什么共同点?
弹性形变——弹力
一、建立概念
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
二、提出问题
关于弹性势能,你最想知道哪些知识?
弹性势能的大小与哪些因素有关?
怎么计算弹性势能的大小?
有没有什么表达式?
能解决什么?
……
简化
——从最简单最基本的研究对象入手
——弹簧的弹性势能
?
?
A
B
三、进行探究
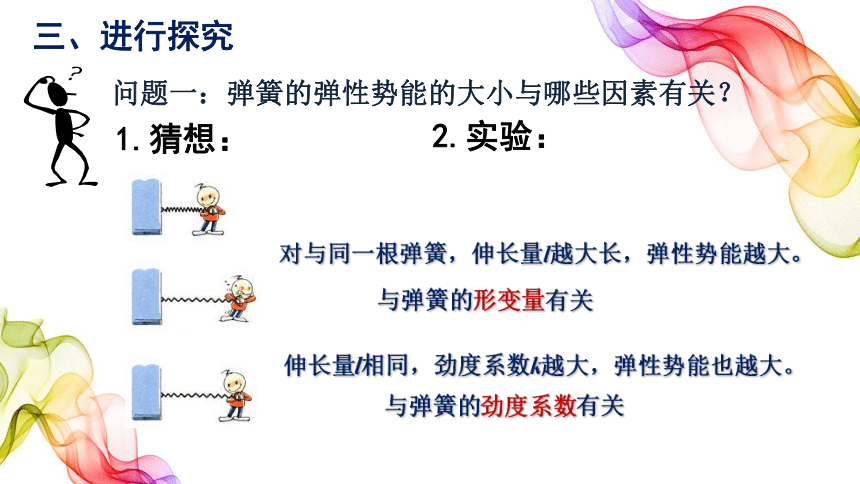
问题一:弹簧的弹性势能的大小与哪些因素有关?
1.猜想:
与弹簧的形变量有关
与弹簧的劲度系数有关
对与同一根弹簧,伸长量l越大长,弹性势能越大。
伸长量l相同,劲度系数k越大,弹性势能也越大。
2.实验:
三、进行探究
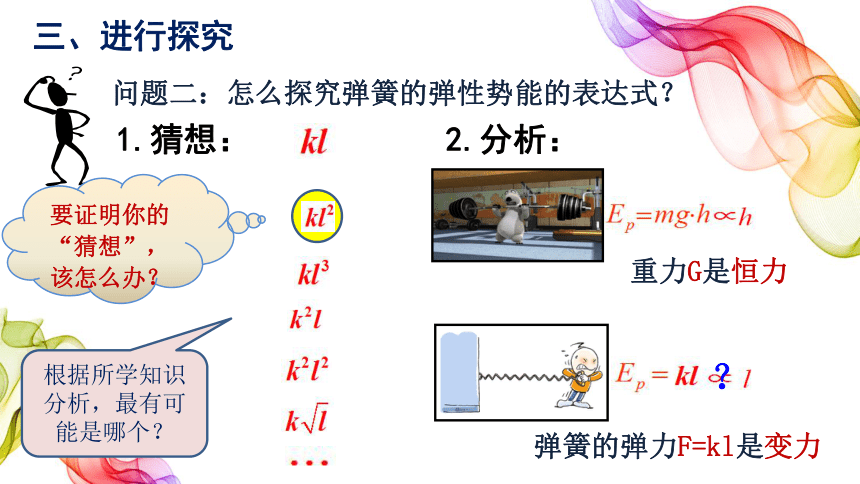
问题二:怎么探究弹簧的弹性势能的表达式?
1.猜想:
2.分析:
重力G是恒力
弹簧的弹力F=kl是变力
根据所学知识分析,最有可能是哪个?
要证明你的“猜想”,该怎么办?
?
三、进行探究
问题二:怎么探究弹簧的弹性势能的表达式?
分析重力做功
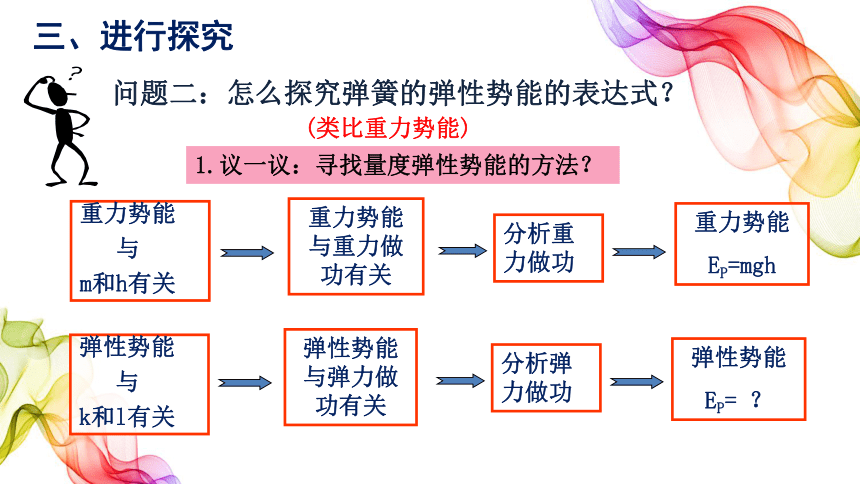
重力势能与重力做功有关
重力势能
EP=mgh
重力势能
与
m和h有关
分析弹力做功
弹性势能与弹力做功有关
弹性势能
EP= ?
弹性势能
与
k和l有关
1.议一议:寻找量度弹性势能的方法?
(类比重力势能)
2.说一说:弹力做功和弹性势能的变化有什么关系?
弹力做正功,弹性势能减少;
弹力做负功,弹性势能增加。
重力做正功,重力势能减少;
重力做负功,重力势能增加。
3.想一想:该怎样选取弹簧的弹性势能的零参考点?
——通常取弹簧处于原长时弹性势能为零
4.探一探:怎样计算弹力做的功?
转化法——缓慢拉动的过程中,拉力做的功等于克服弹力所做的功,等于弹性势能的增加量
怎样解决这个难题?
拉力F 是恒力吗?能用公式W=Flcosa计算吗?
(2)思考讨论:
(1)创设情境:
缓慢拉动弹簧
从A到B分成很多小段
微分思想(化曲为直)
Δl1, Δl2, Δl3…
F1, F2, F3 …
转化思想(化变为恒)
W1=F1Δl1
W2 =F2Δl2
W3=F3Δl3
…
弹力在全过程中所做的功是:
W= W1+W2+W3+…+Wn
F1Δl1
+F2Δl2
+F3Δl3
+…+ FnΔln
=
积分思想
这个式子怎样求和?
(3)联想 I:
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
匀变速直线运动的位移与速度的关系
(4)联想II:
F拉= kl
l
F拉
O
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力做功与弹簧伸长的关系
(5)迁移:
拉力所做的功等于图线与横轴所围的面积!
1.推导:
四、得出结论
o
l
F
拉力所做的功等于图线与横轴所围的面积
拉力做功的表达式:
弹力做功的表达式:
弹力势能的表达式:
2.思考:
通过探究得出的弹簧拉伸时弹性势能的表达式,压缩时适用吗?有无条件限制?
1. 如图所示,小明玩蹦蹦杆。在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是 ( )
A.重力势能减小,弹性势能增大
B.重力势能增大,弹性势能减小
C.重力势能减小,弹性势能减小
D.重力势能不变,弹性势能增大
A
五、巩固练习
2.一物体以初速度v0冲向与竖起墙壁相连的轻质弹簧,墙壁与物体间的弹簧被物体压缩,在此过程中,下列说法正确的是:( )
A. 物体对弹簧的功与弹簧的压缩量成正比
B. 物体向墙壁运动相同的位移,弹力做的功不等
C. 弹力做正功,弹簧的弹性势能减小
D. 弹力做负功,弹簧的弹性势能增加
五、巩固练习
BD
3.如图甲所示,“蹦极”是一项富有刺激性的运动项目。某人身系弹性绳自高空P点自由下落,如图乙所示,a点是弹性绳的原长位置,c点是人所到达的最低点,b点是人静止地悬吊着时的平衡位置。试定性地说明蹦极运动过程中能量的转化情况。
图(甲)
图(乙)
图(丙)
五、巩固练习
与弹力做功的关系
相关因素
表达式
弹性势能
知识层面
方法层面
1. 科学探究方法:
2. 物理思想方法:
类比、迁移、微元法、图像法
六、课堂总结
再见!
5探究弹性势能的
表达式
高一物理
试一试:为什么松手后圆珠笔会跳起来?
有魔力的橡皮筋
想一想:橡皮筋具有魔力的秘密是什么?
三张图中的物体有什么共同点?
弹性形变——弹力
一、建立概念
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
二、提出问题
关于弹性势能,你最想知道哪些知识?
弹性势能的大小与哪些因素有关?
怎么计算弹性势能的大小?
有没有什么表达式?
能解决什么?
……
简化
——从最简单最基本的研究对象入手
——弹簧的弹性势能
?
?
A
B
三、进行探究
问题一:弹簧的弹性势能的大小与哪些因素有关?
1.猜想:
与弹簧的形变量有关
与弹簧的劲度系数有关
对与同一根弹簧,伸长量l越大长,弹性势能越大。
伸长量l相同,劲度系数k越大,弹性势能也越大。
2.实验:
三、进行探究
问题二:怎么探究弹簧的弹性势能的表达式?
1.猜想:
2.分析:
重力G是恒力
弹簧的弹力F=kl是变力
根据所学知识分析,最有可能是哪个?
要证明你的“猜想”,该怎么办?
?
三、进行探究
问题二:怎么探究弹簧的弹性势能的表达式?
分析重力做功
重力势能与重力做功有关
重力势能
EP=mgh
重力势能
与
m和h有关
分析弹力做功
弹性势能与弹力做功有关
弹性势能
EP= ?
弹性势能
与
k和l有关
1.议一议:寻找量度弹性势能的方法?
(类比重力势能)
2.说一说:弹力做功和弹性势能的变化有什么关系?
弹力做正功,弹性势能减少;
弹力做负功,弹性势能增加。
重力做正功,重力势能减少;
重力做负功,重力势能增加。
3.想一想:该怎样选取弹簧的弹性势能的零参考点?
——通常取弹簧处于原长时弹性势能为零
4.探一探:怎样计算弹力做的功?
转化法——缓慢拉动的过程中,拉力做的功等于克服弹力所做的功,等于弹性势能的增加量
怎样解决这个难题?
拉力F 是恒力吗?能用公式W=Flcosa计算吗?
(2)思考讨论:
(1)创设情境:
缓慢拉动弹簧
从A到B分成很多小段
微分思想(化曲为直)
Δl1, Δl2, Δl3…
F1, F2, F3 …
转化思想(化变为恒)
W1=F1Δl1
W2 =F2Δl2
W3=F3Δl3
…
弹力在全过程中所做的功是:
W= W1+W2+W3+…+Wn
F1Δl1
+F2Δl2
+F3Δl3
+…+ FnΔln
=
积分思想
这个式子怎样求和?
(3)联想 I:
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
匀变速直线运动的位移与速度的关系
(4)联想II:
F拉= kl
l
F拉
O
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力做功与弹簧伸长的关系
(5)迁移:
拉力所做的功等于图线与横轴所围的面积!
1.推导:
四、得出结论
o
l
F
拉力所做的功等于图线与横轴所围的面积
拉力做功的表达式:
弹力做功的表达式:
弹力势能的表达式:
2.思考:
通过探究得出的弹簧拉伸时弹性势能的表达式,压缩时适用吗?有无条件限制?
1. 如图所示,小明玩蹦蹦杆。在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是 ( )
A.重力势能减小,弹性势能增大
B.重力势能增大,弹性势能减小
C.重力势能减小,弹性势能减小
D.重力势能不变,弹性势能增大
A
五、巩固练习
2.一物体以初速度v0冲向与竖起墙壁相连的轻质弹簧,墙壁与物体间的弹簧被物体压缩,在此过程中,下列说法正确的是:( )
A. 物体对弹簧的功与弹簧的压缩量成正比
B. 物体向墙壁运动相同的位移,弹力做的功不等
C. 弹力做正功,弹簧的弹性势能减小
D. 弹力做负功,弹簧的弹性势能增加
五、巩固练习
BD
3.如图甲所示,“蹦极”是一项富有刺激性的运动项目。某人身系弹性绳自高空P点自由下落,如图乙所示,a点是弹性绳的原长位置,c点是人所到达的最低点,b点是人静止地悬吊着时的平衡位置。试定性地说明蹦极运动过程中能量的转化情况。
图(甲)
图(乙)
图(丙)
五、巩固练习
与弹力做功的关系
相关因素
表达式
弹性势能
知识层面
方法层面
1. 科学探究方法:
2. 物理思想方法:
类比、迁移、微元法、图像法
六、课堂总结
再见!
