人教版数学八年级上册 (11.1 11.2)三角形有关的边和角讲义(3课时 无答案)
文档属性
| 名称 | 人教版数学八年级上册 (11.1 11.2)三角形有关的边和角讲义(3课时 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览


文档简介
教师辅导讲义
学员编号: 年 级:初一 课 时 数: 3 学员姓名: 辅导科目:数学 学科教师:
授课类型 T同步( 三角形 )
授课日期及时段
教学内容
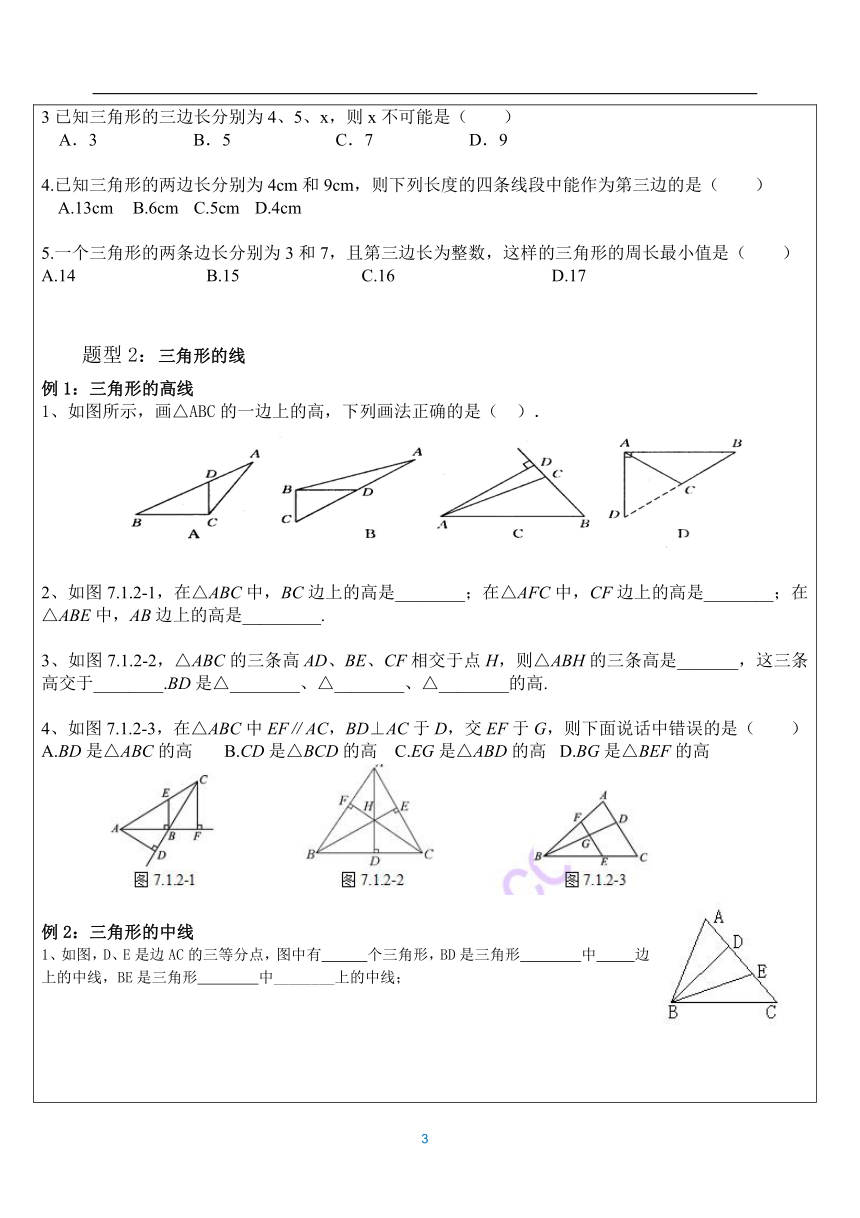
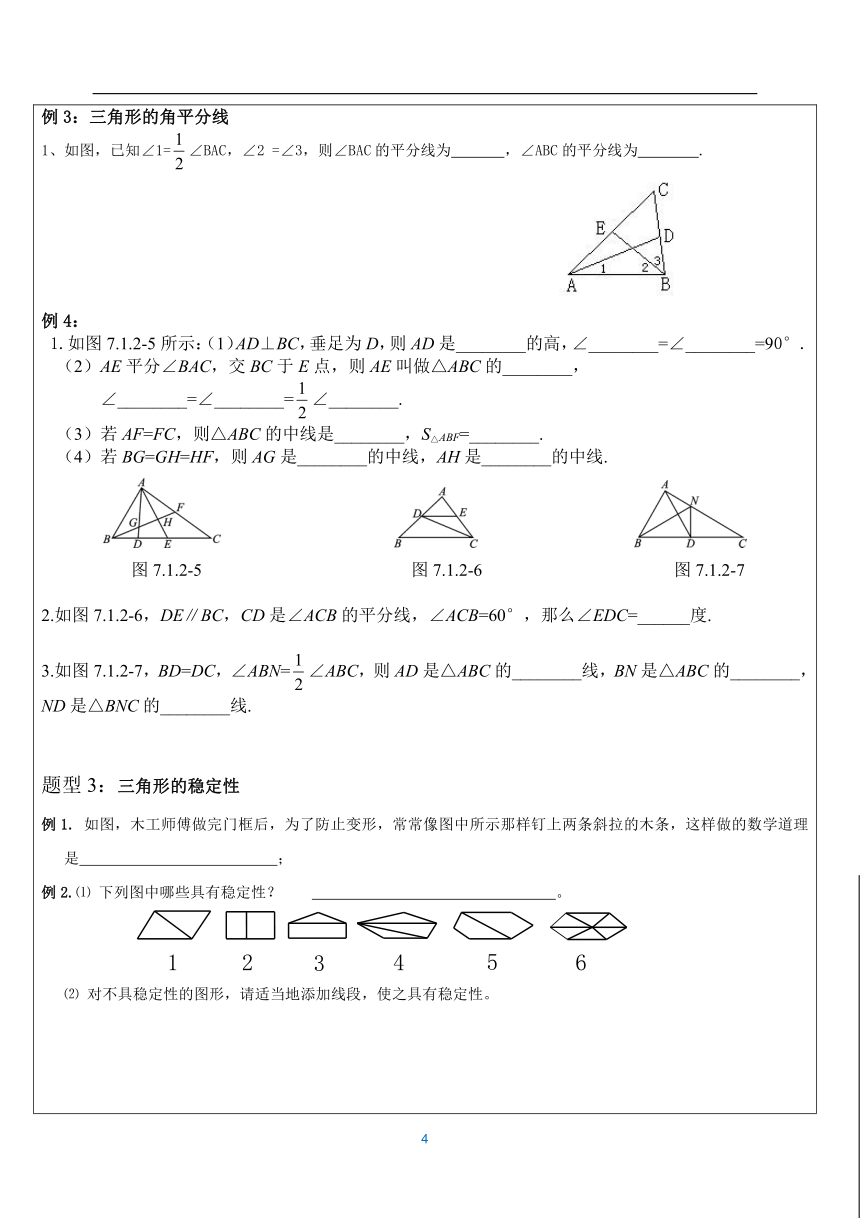
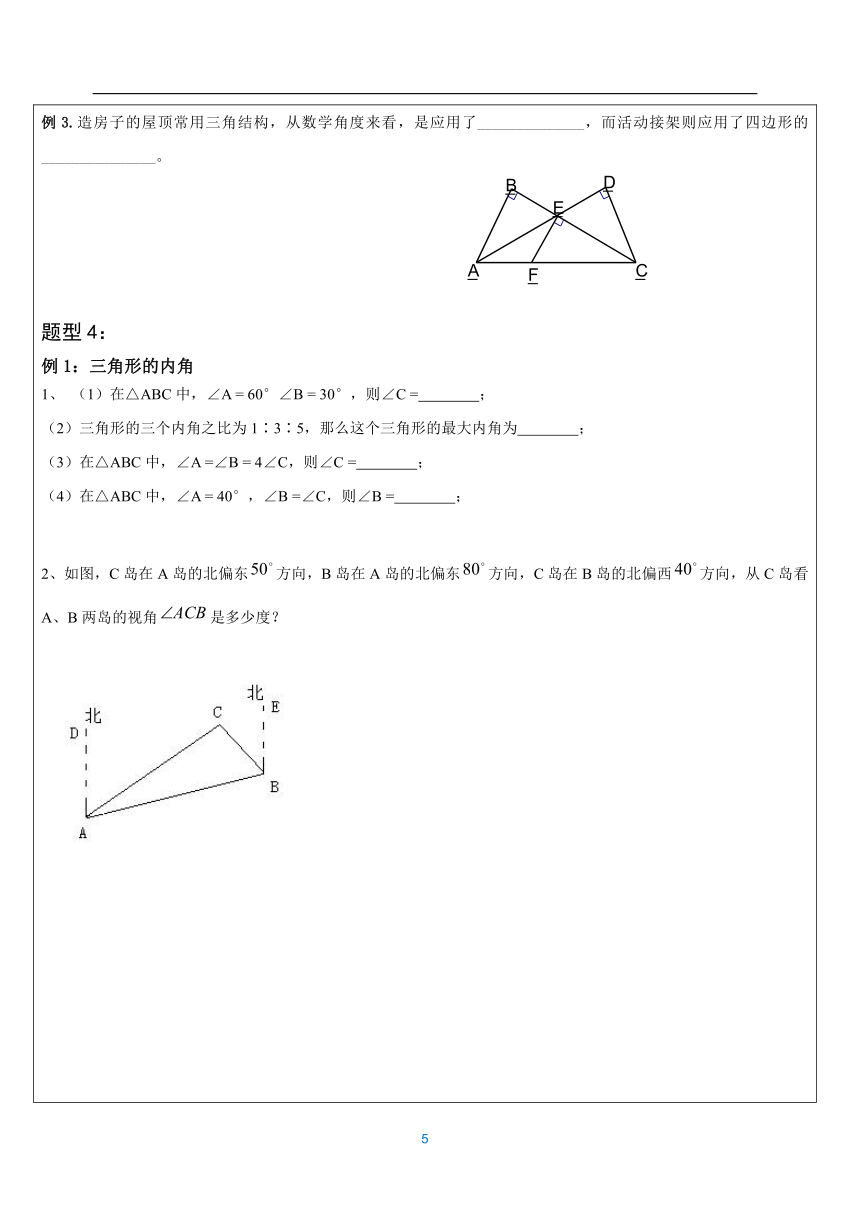
(大脑放电影~) 知识点1:三角形:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。 (用“△”表示) 边:①三边都不相等; 三角形的分类: ②等腰三角形(底边和腰不相等的等腰三角形;等边三角形) 角:①锐角三角形;②直角三角形;③钝角三角形 另两边之差的绝对值<第三边<另两边之和 高线:从三角形的一个顶点向它所对的边所在直线画垂线,顶点和垂足之间的线段 叫做该三角形这条边上的高。(钝角三角形的高线) 中线:三角形,连接一个顶点和它所对的边的中点,所得线段叫做该三角形这条边 上的中线。 角平分线:三角形一个内角的平分线与它的对边相交,所得线段叫做该三角形的角 平分线。 重心:三角形三条中线的交点叫做三角形的重心。 三角形的稳定性:三角形的三条边确定后,三角形的形状就确定不变了。 知识点2:三角形内角和定理:三角形三个内角的和等于180°。 直角三角形的判定:有两个角互余的三角形是直角三角形。 直角三角形的性质:直角三角形的两个锐角互余。 三角形的外角:三角形的一边与另一边的延长线组成的角叫做三角形的外角。 三角形外角的性质:三角形的一个等于与它不相邻的两个内角的和。 (热个身先~~~) 题型1:三角形的三边关系 例1:1、下列长度的三条线段能否组成三角形?为什么? (1)3,4,8; (2)5,6,11; (3)5,6,10有四根木条,长度分别是12cm、10cm、8cm、4cm,选其中三根组成三角形,能组成三角形的个数是_______个。 3、如果三角形的两边长分别是3和5,那么第三边长可能是( ) A、1 B、9 C、3 D、10 4、一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长 例2:1、已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )? A.2cm? B.3cm? C.4cm? D.5cm2.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( ) A.1,2,3 B.2,5,8 C.3,4,5 D.4,5,10 3已知三角形的三边长分别为4、5、x,则x不可能是( )A.3 B.5 C.7 D.94.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( ) A.13cm B.6cm C.5cm D.4cm 5.一个三角形的两条边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )A.14 B.15 C.16 D.17【来源:21·世纪 题型2:三角形的线例1:三角形的高线1、如图所示,画△ABC的一边上的高,下列画法正确的是( ). 2、如图7.1.2-1,在 (?http:?/??/?www.21cnjy.com?)△ABC中,BC边上的高是________;在△AFC中,CF边上的高是________;在△ABE中,AB边上的高是_________.21教育 网3、如图7.1.2-2,△ABC的三条 (?http:?/??/?www.21cnjy.com?)高AD、BE、CF相交于点H,则△ABH的三条高是_______,这三条高交于________.BD是△________、△________、△________的高. W4、如图7.1.2-3,在△ABC中EF∥AC,BD⊥AC于D,交EF于G,则下面说话中错误的是( ) A.BD是△ABC的高 B.CD是△BCD的高 C.EG是△ABD的高 D.BG是△BEF的高 例2:三角形的中线1、如图,D、E是边AC的三等分点,图中有 个三角形,BD是三角形 中 边上的中线,BE是三角形 中________上的中线; 例3:三角形的角平分线1、如图,已知∠1=∠BAC,∠2 =∠3,则∠BAC的平分线为 ,∠ABC的平分线为 . 例4: 1.如图7.1.2-5所示:(1)AD⊥BC,垂足为D,则AD是________的高,∠________=∠________=90°. (2)AE平分∠BAC,交BC于E点,则AE叫做△ABC的________, ∠________=∠________=∠________. (3)若AF=FC,则△ABC的中线是________,S△ABF=________. (4)若BG=GH=HF,则AG是________的中线,AH是________的中线. 图7.1.2-5 图7.1.2-6 图7.1.2-7 如图7.1.2-6,DE∥BC,CD是∠ACB的平分线,∠ACB=60°,那么∠EDC=______度. 3.如图7.1.2-7,BD=DC,∠ABN=∠ABC,则AD是△ABC的________线,BN是△ABC的________,ND是△BNC的________线. 题型3:三角形的稳定性例1. 如图,木工师傅做完门框后,为了防止变形,常常像图中所示那样钉上两条斜拉的木条,这样做的数学道理是 ;例2.⑴ 下列图中哪些具有稳定性? 。 ⑵ 对不具稳定性的图形,请适当地添加线段,使之具有稳定性。 例3.造房子的屋顶常用三角结构,从数学角度来看,是应用了______________,而活动接架则应用了四边形的_______________。 题型4:例1:三角形的内角1、 (1)在△ABC中,∠A = 60°∠B = 30°,则∠C = ; (2)三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为 ; (3)在△ABC中,∠A =∠B = 4∠C,则∠C = ;(4)在△ABC中,∠A = 40°,∠B =∠C,则∠B = ; 2、如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度? 例2:三角形的外角1.若三角形的外角中有一个是锐角,则这个三角形是________三角形. 2.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”). 3.如图1,x=______. (1) (2) (3) 4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________. 5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数 6.如图所示,AE∥BD,∠1=95°,∠2=28°,求∠C 例3:判断题(1) 三角形中最大的角是,那么这个三角形是锐角三角形( ) (2) 一个三角形中最多只有一个钝角或直角( ) (3)一个等腰三角形一定是锐角三角形( ) (4) 一个三角形最少有一个角不大于( ) (你都掌握了没有呢~~~) 检测题:1、如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于 ( )A.50° B.60°C.65° D.90°2、如图,在△ABC中,已知∠A=80°, ∠B=60°,DE∥BC,那么∠CED的大小是 ( )A.40° B.60°C.120° D.140°3、在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是 ( )A.等边三角形 B.锐角三角形C.直角三角形 D.钝角三角形 4、若一个三角形三个内角度数的比为2︰3︰4,那么这个三角形是 ( )A.直角三角形 B.锐角三角形C.钝角三角形 D.等边三角形5、如图,∠1+∠2+∠3+∠4= . 6、已知△ABC的一个外角为50°,则△ABC一定是 ( )A.锐角三角形 B.钝角三角形C.直角三角形 D.锐角三角形或钝角三角形 7、如图所示,将△ABC沿EF折叠,使点C落到点C'处,试探求∠1,∠2与∠C的数量关系. (?http:?/??/?www.21cnjy.com?)若等腰三角形的一边长为3cm,另一边长为4cm,则它的周长为 cm. 9、若等腰三角形的一角为70度?,则它的顶角为 度 直角三角形一直角边是5,斜边上的中线等于6.5,则另一直角 边等于 11、直角三角形的两锐角的平分线相交而成的钝角为 度. 等腰三角形中,和顶角相邻的外角平分线和底边的位置关系是 。 13、在Rt△ABC中,∠B=Rt∠,AB=2cm,AC=3cm,则BC= cm。 14、在△ABC中,AB=AC,BD是角平分线,如果∠A=500,那么∠BDC= 度。 15、三角形的三边分别为、、且满足,则这个三角形(按边分类)一定是 三角形 16、等腰三角形的底边长为10cm,一腰上的中线把这个三角形的周长分为两部分,这两部分之差为4cm,那么这个等腰三角形的腰长是 cm 17、在△ABC中,AB及AC边的垂直平分线相交于O点,∠A=800,则∠BOC= 度。 18、在△ABC中,AB=AC,下列推理中错误的是……………………( )。 A、如果AD是中线,那么AD⊥BC,∠BAD=∠DAC; B、如果BD是高,那么BD是角平分线; C、如果AD是高,那么∠BAD=∠DAC、BD=DC; D、如果AD是角平分线,那么AD也是BC边的垂直平分线 19、下列各组数中,可作为直角三角形的三边长的是 ……………… ( )(A) 2,3,4 (B) 2,2,3 (C) 2,1.5,2.5 (D) 2,1999,2001 20、等腰三角形一腰上的高与底边所夹的角等于……………………( )。 A、顶角 B、顶角的一半 C、顶角的2倍 D、底角的一半 21、AB∥CD,AC⊥BC图中与∠CAB互余的角有几个?请把它们写出来,并说明理由。 22、如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数. 23、已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.www-2-1-cnjy-com 24、、如图,已知△ABC中,∠ABC和∠ACB的平分线BD、CE相交于点O,且∠A=60°,求∠BOC的度数. 21*cnjy*com ( 画竹必先成竹于胸!) 题型一:三角形三边关系1、现有两根木棒的长度分别为40厘米和50厘米,若要钉成一个三角形框架,那么所需木棒的长一定为( ) A.10厘米 B.40厘米 C.90厘米 D.100厘米 2、下面各组中的三条线段能组成三角形的是( ) A、2cm、3cm,5cm B、1cm、6cm、6cm C、2cm、6cm、9cm D、5cm、3cm、10cm有下列长度(cm)的三条小木棒,如果首尾顺次连接,能钉成三角形的是( )
A. 10、14、24 B. 12、16、32
C. 16、6、4 D. 8、10、12 4、如果一个三角形的两边为2和7,且第三边为奇数,则三角形的周长为_______ 5、若等腰三角形两边长分别为2和5,那它的周长是______________. 6、若a,b,c是△ABC的三边,则化简|a﹣b﹣c|+|a﹣c+b|+|a+b+c|=_________. 7、已知△ABC的两条边长分别为4和7,则第三边c的取值范围是_______ 8、一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是( ) A、14 B、15 C、16 D、17 题型二:三角形有关的线段1、三角形三条高的交点一定在( ) A.三角形的内部B.三角形的外部 C.三角形的内部或外部 D.三角形的内部、外部或顶点2、下面四个图形中,线段BE是△ABC的高的图是( ) 3、锐角三角形的三条高都在_______________,钝角三角形有_________条高在三角形外,直角三角形有两条高恰好是它的_______.6、如图,BD是△ABC的中线,AB=6 cm,BC=4 cm,则△ABD和△BCD的周长差为 cm. 7、如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长. 8、画图题:如图所示,在△ABC中,画: (1)AC边上的中线BD,(2)AC边上的高BE,(3)BC边上的高AF。9、如图,在△ABC中,BE⊥AC,BC=5 cm,AC=8 cm,BE=3 cm. (1)求△ABC的面积; (2)画出△ABC中的BC边上的高AD,并求出AD的值. 题型三:与三角形有关的角1、具备下列条件的三角形ABC中,不为直角三角形的是( ) A.∠A+∠B=∠C B.∠A=∠B=∠C C.∠A=90°﹣∠B D.∠A﹣∠B=90° 2、三角形的三个内角中,最小的角不大于( ) A.50° B.30° C.60° D.90° 3、一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( ) A.直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形4、如图,BD平分∠ABC,CD⊥BD,垂足为D,∠C=55°,则∠ABC的度数是( )A.35° B.55° C.60° D.70°5、在△ABC中,∠A=60°,∠C=2∠B,则∠C=______________.6、已知三角形三个内角的度数比是2∶3∶4,则这个三角形中最大角的度数是 . 7、将一副三角板如图叠放,如图中∠为_______°. 8、如图,AB∥CD,∠B=72°,∠D=32°,则∠F=_______________. 9、如图,点P是△ABC内一点,连接BP并延长交AC于D,连接PC,把∠1、∠2、∠A从大到小排列为:( )>( )>( )。 10、如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A=_________°. 12、已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC,求证:AD∥BC。 13、如图B点在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B北偏东80°方向,求∠ACB。 14、如图,已知△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线.求:∠DAE的度数.(写出推导过程) (?http:?/??/?www.jyeoo.com?/??) 15、如图,若AB∥CD,EF与AB,CD分别相交于点E,F, EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,则∠EPF的度数。 稳定性1、下列图形中具有稳定性的是( ) A、正方形 B、长方形 C、钝角三角形 D、菱形2、如图所示是一个起重机的示意图,在起重架中间增加了很多斜条,它所运用的几何原理是________. 三、课堂达标检测1、以下列各组线段为边,能组成三角形的是( ) A. B. C. D. 2、如图,图中共有三角形的个数是( ) A. 3 B. 4 C. 5 D. 6 3、一个三角形的两边长分别是3和8,周长是偶数,那么第三边边长是 .4、长度分别为2、7、的三条线段能组成一个三角形,的值可以是( ) A.4 B.5 C.6 D.95、已知△ABC的两条边长分别为4和7,则第三边c的取值范围是___________6、若是△ABC的三边,请化简___________.如图1四个图形中,线段BE是△ABC的高的图是( )8、如图所示,AD是△ABC的高,延长BC至E,使CE=BC,△ABC的面积为S1 ,△ACE的面积为S2 ,那么( ) A.S1 >S2 B.S1 =S2 C.S1 <S2 D.不能确定 第8题 9、已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为20,则△ABE的面积为( )A.5 B.10 C.15 D.18 10、已知△ABC中,为钝角.请你按要求作图(不写作法,但要保留作图痕迹): (1)过点A作BC的垂线AD;(2)作的角平分线交AC于E;(3)取AB中点F,连结CF. 11、一个三角形的三个内角中( ) A、至少有一个角等于90° B、至少有一个角大于90° C、不可能有两个角都大于89° D、不可能都小于60° 12、适合条件∠A=∠B=∠C的三角形一定是( )A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形 13、如图,AD是几个三角形的高?( )A.?4 B.?5? C.?6 D.?7 14、设△ABC的三边长分别为a、b、c,其中a、b满足|a+b-4|+(a-b+2)2=0,则第三边的长c的取值范围是( )A.?3<c<5 ?B.?2<c<3 C.?1<c<4 D.?2<c<4 15、一个三角形的两边的长分别为3和8,第三边的长为奇数,则第三边的长为( )A.?5或7 B.?7 C.?9 D.?7或9 16、如果三角形的两边长分别为3和5,则周长L的取值范围是( )A.?6<L<15 B.?6<L<16 C.?11<L<13 D.?10<L<16 17、如图,△ABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD与BE交于点F,则∠AFB的度数是( ) A.126° B.120° C.116° D.110° 18、如图,∠D=30°,∠O=50°,∠C=35°,则∠AEC等于_________ 19、如图,已知点D为△ABC的边BC延长线上一点,DF⊥AB于点F交AC于点E,∠A=35°,∠D=42°.求∠ACD的度数. 20、如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数。 21、用两种方法证明“三角形的外角和等于360°”:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°. 专题精讲1、一个五角星ABCDE,如图(1)所示,你能求出∠A+∠B+∠C+∠D+∠E的度数吗? (2)变式一:如果B点向下移动到AC上,如图(2)所示,你能求出∠A+∠EBD+∠C+∠D+∠E的度数吗? (3)变式二:如果B点继续向下,移到AC的另一侧,如图(3)所示,变式一中的结果还成立吗? 2、一个正六边形和两个等边三角形的位置如图所示,∠3=70°,则∠1+∠2= . 3、已知:△ABC,如图,若P点是∠ABC和∠ACB的角平分线的交点,求证:∠P=90°+∠A. 4、如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°?∠A. 5、如图,点P为△ABC内角平分线BP与外角平分线CP的交点,请写出∠BPC与∠A的关系; 专题过关1、如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=_________ 2、如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为________ 3、如图,△ABC的内角平分线BP与外角平分线CP交于P,∠A=68?,则∠P=( )
A.?22 B.?34 C.?68 D.?564、如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018=_________.5、如图所示,∠1+∠2+∠3+∠4+∠5+∠6=_________度.
T同步——三角形同步训练
同步知识梳理
同步题型分析
教师备课札记
1
2
3
4
5
6
_
F
_
A
_
D
_
C
_
B
_
E
课堂达标检测
C专题——三角形模型
知识典例
