人教版数学八年级下册19.1变量与函数讲义(2课时 无答案)
文档属性
| 名称 | 人教版数学八年级下册19.1变量与函数讲义(2课时 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 481.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 16:22:37 | ||
图片预览

文档简介
教师辅导讲义
学员编号: 年 级: 初二 课 时 数: 学员姓名: 辅导科目: 数学 学科教师:
授课类型 T同步( 函数 ) C专题( 函数图像 )
授课日期及时段 2020年
教学内容
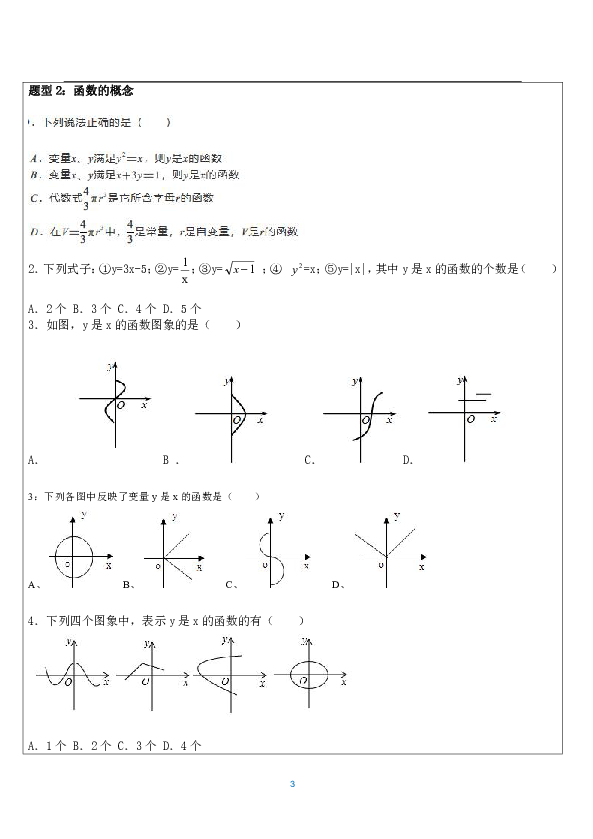
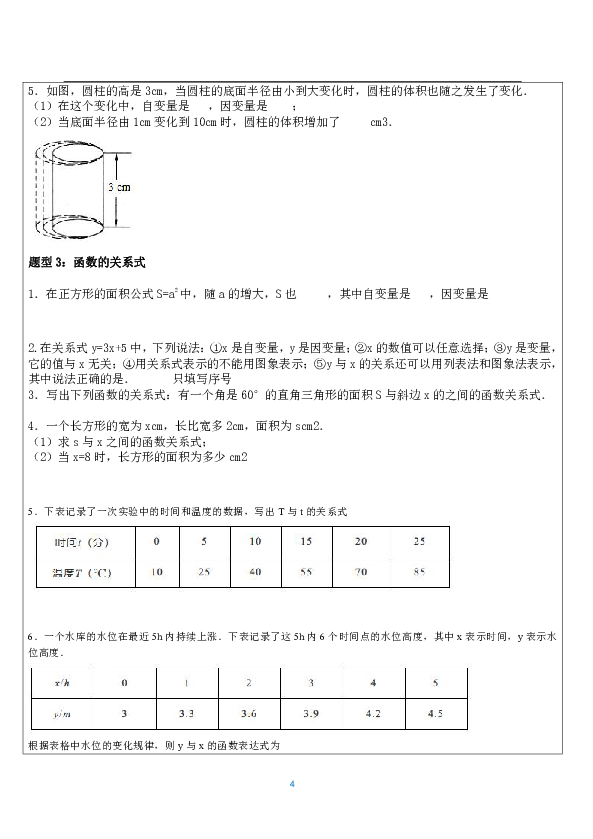
(大脑放电影~) 1.变量的定义:在某一变化过程中,我们称数值发生变化的量为变量。 变量还分为自变量和因变量。 自变量:引起变化的量。因变量:某些特定的数会随另一个(或另几个)会变动的数的变动而变动,就称为因变量。常量的定义:在某一变化过程中,有些量的数值始终不变,我们称它们为常量。 3.函数的定义:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数,y的值称为函数值. 4.函数的三种表示法:(1)表达式法(解析式法);(2)列表法;(3)图象法.用数学式子表示函数的方法叫做表达式法(解析式法)。由一个函数的表达式,列出函数对应值表格来表示函数的方法叫做列表法。把这些对应值(有序的)看成点坐标,在坐标平面内描点,进而画出函数的图象来表示函数的方法叫做图像法。 5.求函数的自变量取值范围的方法.(1)要使函数的表达式有意义:整式(多项式和单项式)时为全体实数;分式时,让分母≠0;含二次根号时,让被开方数≠0 。(2)对实际问题中的函数关系,要使实际问题有意义。注意可能含有隐含非负或大于0的条件。 6.求函数值方法:把所给自变量的值代入函数表达式中,就可以求出相应的函数值.7.描点法画函数图象的一般步骤如下: Step1:列表(表中给出一些自变量的值及其对应的函数值); Step2:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点); Step3:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来). 8.判断y是不是x的函数的题型给出解析式让你判断:可给x值来求y的值,若y的值唯一确定,则y是x的函数;否则不是。给出图像让你判断:过x轴做垂线,垂线与图像交点多余一个(≥2)时,y不是x的函数;否则y是x的函数。 (热个身先~~~) 题型1:常量与变量1.表示两个变量之间的关系,下列说法错误的是( ) A.用表格可以表示任意两个变量之间的关系 B.用关系式可以表示任意两个变量之间的关系 C.用图象可以表示任意两个变量之间的关系 D.在某一变化过程中,数值始终不变的量叫常量 2.在圆的周长C=2πR中,常量与变量分别是( ) A.2是常量,C、π、R是变量 B.2π是常量,C、R是变量 C.C、2是常量,R是变量 D.2是常量,C、R是变量 水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长与直径的比)为π,指出其中的变量为 .4.矩形的面积为,则长和宽之间的关系为 ,当长一定时, 是常量, 是变量. 题型2:函数的概念 2.下列式子:①y=3x-5;②y=;③y= ;④=x;⑤y=|x|,其中y是x的函数的个数是( ) A.2个 B.3个 C.4个 D.5个 3.如图,y是x的函数图象的是( ) B . C.D.3:下列各图中反映了变量y是x的函数是( )? B、? C、? D、? 4.下列四个图象中,表示y是x的函数的有( ) A.1个 B.2个 C.3个 D.4个 5.如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化. (1)在这个变化中,自变量是 ,因变量是 ; (2)当底面半径由1cm变化到10cm时,圆柱的体积增加了 cm3.题型3:函数的关系式 1.在正方形的面积公式S=a2中,随a的增大,S也 ,其中自变量是 ,因变量是 2.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是. 只填写序号 3.写出下列函数的关系式:有一个角是60°的直角三角形的面积S与斜边x的之间的函数关系式. 4.一个长方形的宽为xcm,长比宽多2cm,面积为scm2. (1)求s与x之间的函数关系式; (2)当x=8时,长方形的面积为多少cm2 5.下表记录了一次实验中的时间和温度的数据,写出T与t的关系式 6.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度. 根据表格中水位的变化规律,则y与x的函数表达式为 7.在一次实验中,马达同学把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值. (1)上表反映了哪两个变量之间的关系, 自变量是 , 因变量是 . (2)当所挂物体重量为3千克时,弹簧长 ;不挂重物时弹簧长 . (3)弹簧长度y与所挂物体质量x之间的关系可以用式子表示为: 题型4:函数的自变量取值范围1.函数中自变量的取值范围为 .2.函数,自变量x的取值范围 。3.圆的面积中,自变量的取值范围是 . 4.函数的自变量x取值范围是 5.若整数x满足|x|≤4,则使函数y=有意义的x的值是 (只需填一个).6.已知等腰三角形的周长为20,设三角形的腰长为x,底边长为y,求y关于x的函数关系式,并写出自变量x的取值范围?题型5:函数值 1.函数中,当时, ,当时, . 2.对于函数y=,当y=2时,x= 3.已知f(x)=,如果f(a)=,那么a= 4.设函数f(x)=x(x-1),以下结论正确的是( ) A.f(a)+f(-a)=0 B.若f(a)=a,则a=0 C.f(a)f( )=1 D.f(a)=f(1-a) 5.某计算程序编辑如图所示,当输入x= 时,输出的y=3. 6.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y=,如果某一温度的摄氏度数是25℃,那么它的华氏度数是 ℉. 7.根据下面的运算程序,若输入x=2-时,输出的结果y= 8.已知水池中有800立方米的水,每小时抽50立方米. (1)写出剩余水的体积立方米与时间(时)之间的函数关系式. (2)写出自变量的取值范围. (3)10小时后,池中还有多少水? (4)几小时后,池中还有100立方米的水? 题型6:函数的图像 1.如图,一个函数的图象由射线BA、线段BC、射线CD组成,其中点A(-2,2),B(1,3),C(2,1),D(6,5),则此函数( ) A.当x<2时,y随x的增大而增大 B.当x<2时,y随x的增大而减小 C.当x>2时,y随x的增大而增大 D.当x>2时,y随x的增大而减小 2.如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( ) A. B. C. D. 3、摩天轮可抽象成一个圆,圆上一点离地面的高度()与旋转时间()之间的关系如图所示。(1)根据图填表。?(2)变量是的函数吗?为什么。(3)根据图中的信息,请写出摩天轮的直径。 4.某市第五中学校办工厂今年产值是15万元,计划今后每年增加2万元.(1)写出年产值(万元)与今后年数之间的函数关系式. (2)画出函数图象. (3)求5年后的年产值. 5.请用学过的方法研究一类新函数(为常数,)的图象和性质。(1)在给出的平面直角坐标系中画出函数的图象。(2)对于函数,当自变量的值增大时,函数值怎样变化。 题型7:动点问题的函数图像 1.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式 .2.如图(1),在矩形ABCD中,动点M从点B出发,沿B→C→D→A方向运动至点A处停止,设点M运动的路程为x,△ABM的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( ) A.55 B.30 C.16 D.6 3.如图,正方形ABCD的边长为4,P为正方形边上一动点,它沿A→D→C→B→A的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映变量y与变量x的关系图象的是( ) A. B. C.D. 4.芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( ) 5.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为千米/小时,特快车的速度为千米/小时,甲、乙两地之间的距离为千米,两车同时出发,则图中折线大致表示两车之间的距离(千米)与快车行驶时间(小时)之间的函数图象是(??)。A:? B:? C:? D:?6.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家的距离与时间之间的关系的图象是 .(只需填序号)(你都掌握了没有呢~~~) 1.矩形的面积为,则长和宽之间的关系为 ,当长一定时, 是常量, 是变量. 2.飞船每分钟转30转,用函数解析式表示转数和时间之间的关系式是 . 3.函数中自变量的取值范围是 . 4.函数中,当时, ,当时, .5.点在函数的图象上,则点的坐标是 .6.函数中自变量的取值范围为 .7.下列:①;②;③;④,具有函数关系(自变量为)的是 .8.圆的面积中,自变量的取值范围是 .9.在圆的周长公式中,下列说法错误的是( ) A.是变量,2是常量 B.是变量,是常量 C.是自变量,是的函数 D.将写成,则可看作是自变量,是的函数 10.在下表中,设表示乘公共汽车的站数,表示应付的票价(元)(站) 1 2 3 4 5 6 7 8 9 10 (元) 1 1 2 2 2 3 3 3 4 4 根据此表,下列说法正确的是( ) A.是的函数 B.不是的函数 C.是的函数 D.以上说法都不对 11.边形的内角和,其中自变量的取值范围是( ) A.全体实数 B.全体整数 C. D.大于或等于3的整数 12.油箱中有油20升,油从管道中匀速流出,100分钟流成.油箱中剩油量(升)与流出的时间(分)间的函数关系式是( ) A. B. C. D.13.根据下表写出函数解析式( ) A. B. C. D.14.如果每盒圆珠笔有12支,售价为18元,那么圆珠笔的售价(元)与支数之间的函数关系式为( ) A. B. C. D.15.设等腰三角形(两底角相等的三角形)顶角的度数为,底角的度数为,则有( )A.(为全体实数) B. C. D.16.下列有序实数对中,是函数中自变量与函数值的一对对应值的是( ) A. B. C. D. 17.如图3所示,结合表格中的数据回答问题: 梯形个数 1 2 3 4 5… 图形周长 5 8 11 14 17… (1)设图形的周长为,梯形的个数为,试写出与的函数解析式. (2)求当时的图形的周长.
T同步——函数同步训练
同步知识梳理
同步题型分析
课堂达标检测
1
