人教版必修二 7.7动能和动能定理(共26张PPT)
文档属性
| 名称 | 人教版必修二 7.7动能和动能定理(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 820.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-25 20:13:17 | ||
图片预览







文档简介
(共26张PPT)
第七章 机械能守恒定律
7.7 动能和动能定理
知识回顾
功能思想:做功与能量变化相关联
特殊情况下力对物体做的功与速度变化的关系
即W∝V 2
一、动能表达式包含的因子
1.动能表达式可能包含V 2这个因子。
2.动能表达式还包含物体自身质量这个因子。
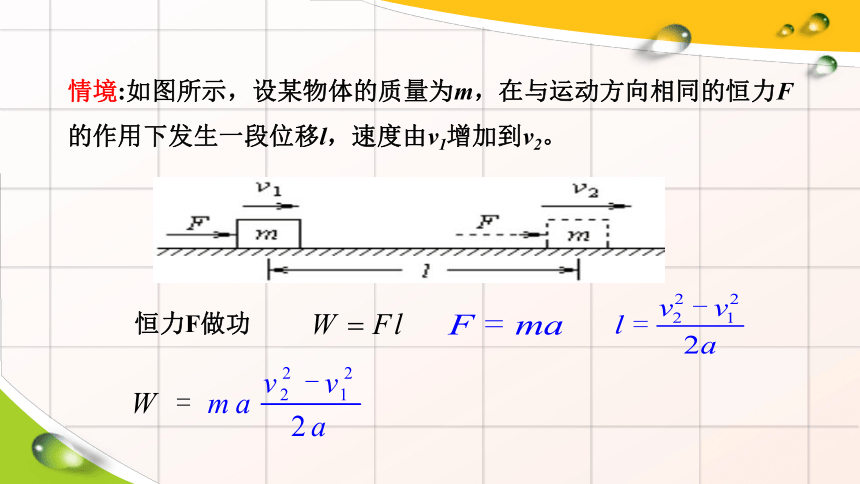
情境:如图所示,设某物体的质量为m,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到v2。
恒力F做功
思考:“ ”是否具有特殊意义的物理量?
这个量在过程终了与过程开始的差正好等于对物体做的功。
上节课的实验表明,力对初速度为0的物体所做的功与物体速度的二次方成正比,可以相互印证。
应该是我们寻找的动能的表达式。
证据:
结论:
2.表达式:
二、动能
1.概念:物体由于运动而具有的能叫做动能。物体的动能等于物体的质量与物体速度的二次方的乘积的一半。
3.单位:焦(J)
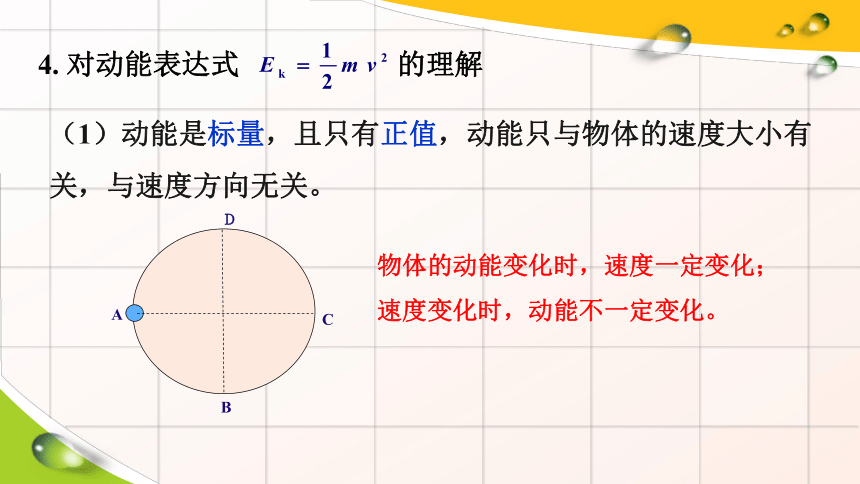
(1)动能是标量,且只有正值,动能只与物体的速度大小有关,与速度方向无关。
4. 对动能表达式 的理解
A
D
C
B
物体的动能变化时,速度一定变化;
速度变化时,动能不一定变化。
(2)动能是状态量,v是瞬时速度。
在某一时刻,物体具有一定的速度,物体的运动状态一定, 物体的动能一定,动能是反映物体本身运动状态的物理量。
4. 对动能表达式 的理解
(3)动能具有相对性,对不同的参考系,物体速度有不同的瞬时值,也就具有不同的动能,不作说明一般都以地面为参考系研究物体的运动。
运动是相对的。当鸟儿与飞机相对而行时,虽然鸟儿的速度不是很大,但是飞机的飞行速度很大,这样对于飞机来说,鸟儿的动能就很大。如果是一只1.8千克的鸟撞在速度为每小时 700千米的飞机上,产生的冲击力比炮弹的冲击力还要大。
鸟击落飞机
4. 对动能表达式 的理解
三、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化,这个结论叫做动能定理。
末状态动能
初状态动能
(1)如果物体受到几个力作用,动能定理中的W表示的物理意义是什么?
2.对动能定理的理解
动能定理表述为:合 力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
合力所做的总功。
W合=Ek2-Ek1
W=W1+W2+W3+…
W=F合lcos α
2.对动能定理的理解
(2)动能是标量,只有正值,但ΔEk有正负之分
当外力做正功时,W>0, ΔEk>0,Ek2>Ek1,即动能增加;
当外力做负功时,W<0,ΔEk<0,Ek22.对动能定理的理解
(3)对状态与过程关系的理解
功是过程量,而动能是状态量;
动能定理表示了过程量等于状态量的改变量的定量关系。
2.对动能定理的理解
(4)动能定理是否可以应用于变力做功或物体做曲线运动的情况?
根据化变为恒、化曲为直的思想,把过程分解为无穷对小段,认为物体在每小段运动中受到的力处理成恒力,运动的轨迹处理成一小段直线,这样累积后就能得到动能定理,因此动能定理可以应用于变力或曲线运动。
(1)明确研究对象及所研究的物理过程。
(2)对研究对象进行受力分析,并确定各力所做的功,求出这些力的功的代数和。
(4)求解方程、分析结果。
3.应用动能定理解题的步骤:
(3)确定始、末状态的动能(未知量用符号表示),根据动能定理列出方程 。
W合=Ek2-Ek1
例1.下列几种情况中,甲、乙两物体的动能相等的是( )
A.甲的速度是乙的2倍,乙的质量是甲的2倍
B.甲的质量是乙的2倍,乙的速度是甲的2倍
C.甲的质量是乙的4倍,乙的速度是甲的2倍
D.质量相同,速度大小也相同,但甲向东运动,乙向西运动
CD
例2.一个小球从高处自由落下,则球在下落过程中的动能( )
A.与它下落的距离成正比
B.与它下落距离的平方成正比
C.与它运动的时间成正比
D.与它运动时间的平方成正比
AD
例3. 如图所示,在高为H的平台上以初速v0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( )
A.
B.
C.
D.
D
m
例4.一架喷气式飞机,质量m=5×103 kg,当起飞过程中从静止开始滑跑的路程为l=5.3×102m时,达到起飞速度v=60m/s,在此过程中飞机受到的平均阻力是飞机重量的k倍(k =0.02),求飞机受到的牵引力。
解:方法一
1找对象(常是单个物体)
方法二 解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F1
F2
3确定各力做功
4运动情况分析
5建方程
2受力分析
解:
例5.在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为( )
C
不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关,在涉及有关的力学问题,优先应用动能定理。
例6.一质量为?m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置B点很缓慢地移动到A点,细线偏离竖直方向的角度为α,如图所示。则拉力F做的功是( )
A. mgLcos θ
B. mgL(1-cos θ)
C. Flcos θ
D. FL
B
例7.质量为m的跳水运动员从高为H的跳台上以速率v1 起跳,落水时的速率为v2 ,运动中遇有空气阻力,那么运动员起跳后在空中运动克服空气阻力所做的功是多少?
V1
H
V2
解:
对象—运动员
过程---从起跳到落水
受力分析---如图所示
f
mg
由动能定理
f
G
G
H
h
分析:小球的下落过程根据受力情况可分为两段:
例8.一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
因此可以分两段求解,也可以按全过程求解
接触地面前做自由落体运动,只受重力G作用;
接触地面后做减速运动,受重力G和阻力f作用。
接触地面前
(2)全过程:
解:以球为研究对象,在下落的过程中受力如图,根据动能定理有
解得:
(1)分段求解
设小球在接触地面时的速度为v,则
接触地面后
G
f
G
H
h
课堂小结
一、动能
1.定义:物体由于运动而具有的能量叫做动能.
2.表达式:
3.单位:焦耳(J)
二、动能定理
1.内容:合力所做的功等于物体动能的变化
2.表达式:
W合=Ek2-Ek1
第七章 机械能守恒定律
7.7 动能和动能定理
知识回顾
功能思想:做功与能量变化相关联
特殊情况下力对物体做的功与速度变化的关系
即W∝V 2
一、动能表达式包含的因子
1.动能表达式可能包含V 2这个因子。
2.动能表达式还包含物体自身质量这个因子。
情境:如图所示,设某物体的质量为m,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到v2。
恒力F做功
思考:“ ”是否具有特殊意义的物理量?
这个量在过程终了与过程开始的差正好等于对物体做的功。
上节课的实验表明,力对初速度为0的物体所做的功与物体速度的二次方成正比,可以相互印证。
应该是我们寻找的动能的表达式。
证据:
结论:
2.表达式:
二、动能
1.概念:物体由于运动而具有的能叫做动能。物体的动能等于物体的质量与物体速度的二次方的乘积的一半。
3.单位:焦(J)
(1)动能是标量,且只有正值,动能只与物体的速度大小有关,与速度方向无关。
4. 对动能表达式 的理解
A
D
C
B
物体的动能变化时,速度一定变化;
速度变化时,动能不一定变化。
(2)动能是状态量,v是瞬时速度。
在某一时刻,物体具有一定的速度,物体的运动状态一定, 物体的动能一定,动能是反映物体本身运动状态的物理量。
4. 对动能表达式 的理解
(3)动能具有相对性,对不同的参考系,物体速度有不同的瞬时值,也就具有不同的动能,不作说明一般都以地面为参考系研究物体的运动。
运动是相对的。当鸟儿与飞机相对而行时,虽然鸟儿的速度不是很大,但是飞机的飞行速度很大,这样对于飞机来说,鸟儿的动能就很大。如果是一只1.8千克的鸟撞在速度为每小时 700千米的飞机上,产生的冲击力比炮弹的冲击力还要大。
鸟击落飞机
4. 对动能表达式 的理解
三、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化,这个结论叫做动能定理。
末状态动能
初状态动能
(1)如果物体受到几个力作用,动能定理中的W表示的物理意义是什么?
2.对动能定理的理解
动能定理表述为:合 力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
合力所做的总功。
W合=Ek2-Ek1
W=W1+W2+W3+…
W=F合lcos α
2.对动能定理的理解
(2)动能是标量,只有正值,但ΔEk有正负之分
当外力做正功时,W>0, ΔEk>0,Ek2>Ek1,即动能增加;
当外力做负功时,W<0,ΔEk<0,Ek2
(3)对状态与过程关系的理解
功是过程量,而动能是状态量;
动能定理表示了过程量等于状态量的改变量的定量关系。
2.对动能定理的理解
(4)动能定理是否可以应用于变力做功或物体做曲线运动的情况?
根据化变为恒、化曲为直的思想,把过程分解为无穷对小段,认为物体在每小段运动中受到的力处理成恒力,运动的轨迹处理成一小段直线,这样累积后就能得到动能定理,因此动能定理可以应用于变力或曲线运动。
(1)明确研究对象及所研究的物理过程。
(2)对研究对象进行受力分析,并确定各力所做的功,求出这些力的功的代数和。
(4)求解方程、分析结果。
3.应用动能定理解题的步骤:
(3)确定始、末状态的动能(未知量用符号表示),根据动能定理列出方程 。
W合=Ek2-Ek1
例1.下列几种情况中,甲、乙两物体的动能相等的是( )
A.甲的速度是乙的2倍,乙的质量是甲的2倍
B.甲的质量是乙的2倍,乙的速度是甲的2倍
C.甲的质量是乙的4倍,乙的速度是甲的2倍
D.质量相同,速度大小也相同,但甲向东运动,乙向西运动
CD
例2.一个小球从高处自由落下,则球在下落过程中的动能( )
A.与它下落的距离成正比
B.与它下落距离的平方成正比
C.与它运动的时间成正比
D.与它运动时间的平方成正比
AD
例3. 如图所示,在高为H的平台上以初速v0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( )
A.
B.
C.
D.
D
m
例4.一架喷气式飞机,质量m=5×103 kg,当起飞过程中从静止开始滑跑的路程为l=5.3×102m时,达到起飞速度v=60m/s,在此过程中飞机受到的平均阻力是飞机重量的k倍(k =0.02),求飞机受到的牵引力。
解:方法一
1找对象(常是单个物体)
方法二 解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F1
F2
3确定各力做功
4运动情况分析
5建方程
2受力分析
解:
例5.在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为( )
C
不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关,在涉及有关的力学问题,优先应用动能定理。
例6.一质量为?m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置B点很缓慢地移动到A点,细线偏离竖直方向的角度为α,如图所示。则拉力F做的功是( )
A. mgLcos θ
B. mgL(1-cos θ)
C. Flcos θ
D. FL
B
例7.质量为m的跳水运动员从高为H的跳台上以速率v1 起跳,落水时的速率为v2 ,运动中遇有空气阻力,那么运动员起跳后在空中运动克服空气阻力所做的功是多少?
V1
H
V2
解:
对象—运动员
过程---从起跳到落水
受力分析---如图所示
f
mg
由动能定理
f
G
G
H
h
分析:小球的下落过程根据受力情况可分为两段:
例8.一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
因此可以分两段求解,也可以按全过程求解
接触地面前做自由落体运动,只受重力G作用;
接触地面后做减速运动,受重力G和阻力f作用。
接触地面前
(2)全过程:
解:以球为研究对象,在下落的过程中受力如图,根据动能定理有
解得:
(1)分段求解
设小球在接触地面时的速度为v,则
接触地面后
G
f
G
H
h
课堂小结
一、动能
1.定义:物体由于运动而具有的能量叫做动能.
2.表达式:
3.单位:焦耳(J)
二、动能定理
1.内容:合力所做的功等于物体动能的变化
2.表达式:
W合=Ek2-Ek1
