2020年春季苏科版数学八下第9章《中心对称图形——平行四边形》单元检测试题(带详细答案)
文档属性
| 名称 | 2020年春季苏科版数学八下第9章《中心对称图形——平行四边形》单元检测试题(带详细答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览


文档简介
2020年春季苏科新版八下第9章《中心对称图形——平行四边形》
单元检测试题
满分100分
班级___________姓名____________学号____________
题号 一 二 三 总分
得分
一.选择题(共8小题,每小题3分,满分24分)
1.下列我国著名企业商标图案中,是中心对称图形的是( )
A. B.
C. D.
2.在俄罗斯方块游戏中,已拼好的图案如图所示,现出现一小方格体正向下运动,你必须进行以下( )操作,才能拼成一个完整图案,使所有图案消失.
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
3.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是( )
A.6 B.5 C.4 D.3
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AB∥CD,∠B=∠D D.AB∥CD,AD=BC
5.如图,平行四边形ABCD中,∠ABC的平分线BE交AD于E,AB=3,BC=8,则DE的长( )
A.4 B.5 C.5.5 D.6
6.下列说法正确的是( )
A.有两个角为直角的四边形是矩形
B.矩形的对角线相等
C.平行四边形的对角线相等
D.对角线互相垂直的四边形是菱形
7.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为( )
A.2 B.3 C.4 D.5
8.如图,平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
A.1 次 B.2次 C.3次 D.4次
二.填空题(共8小题,每小题3分,满分24分)
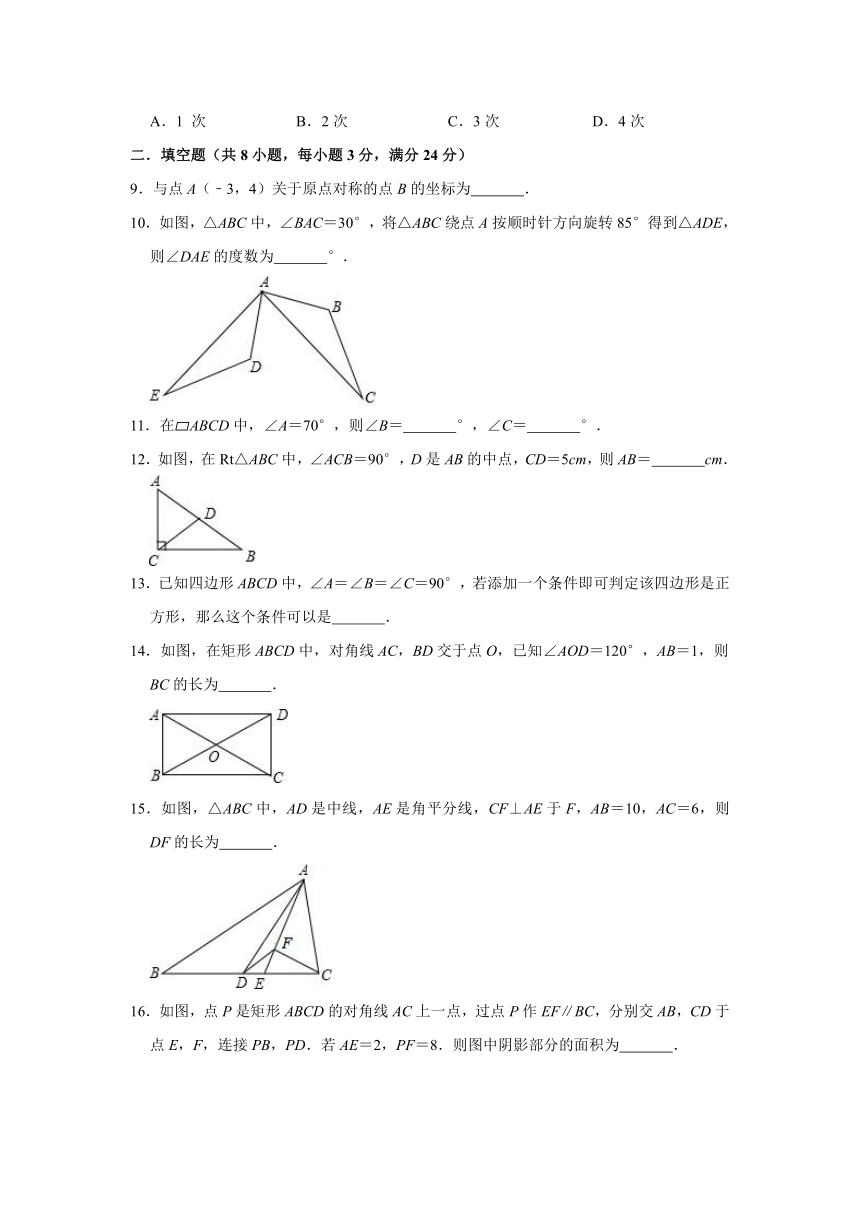
9.与点A(﹣3,4)关于原点对称的点B的坐标为 .
10.如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°得到△ADE,则∠DAE的度数为 °.
11.在?ABCD中,∠A=70°,则∠B= °,∠C= °.
12.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=5cm,则AB= cm.
13.已知四边形ABCD中,∠A=∠B=∠C=90°,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是 .
14.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为 .
15.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为 .
16.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 .
三.解答题(共6小题,17-20每小题8分,21-22每小题10分,满分52分)
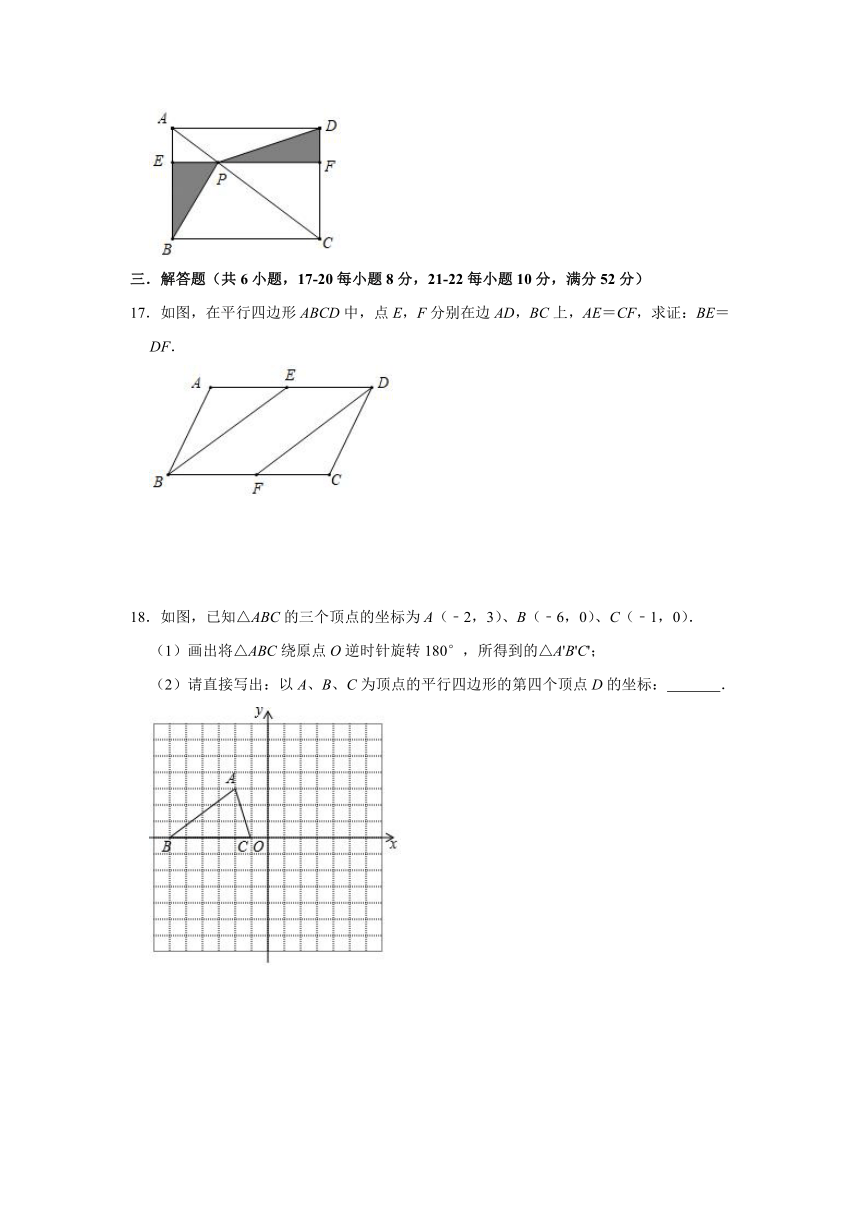
17.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:BE=DF.
18.如图,已知△ABC的三个顶点的坐标为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出将△ABC绕原点O逆时针旋转180°,所得到的△A'B'C';
(2)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标: .
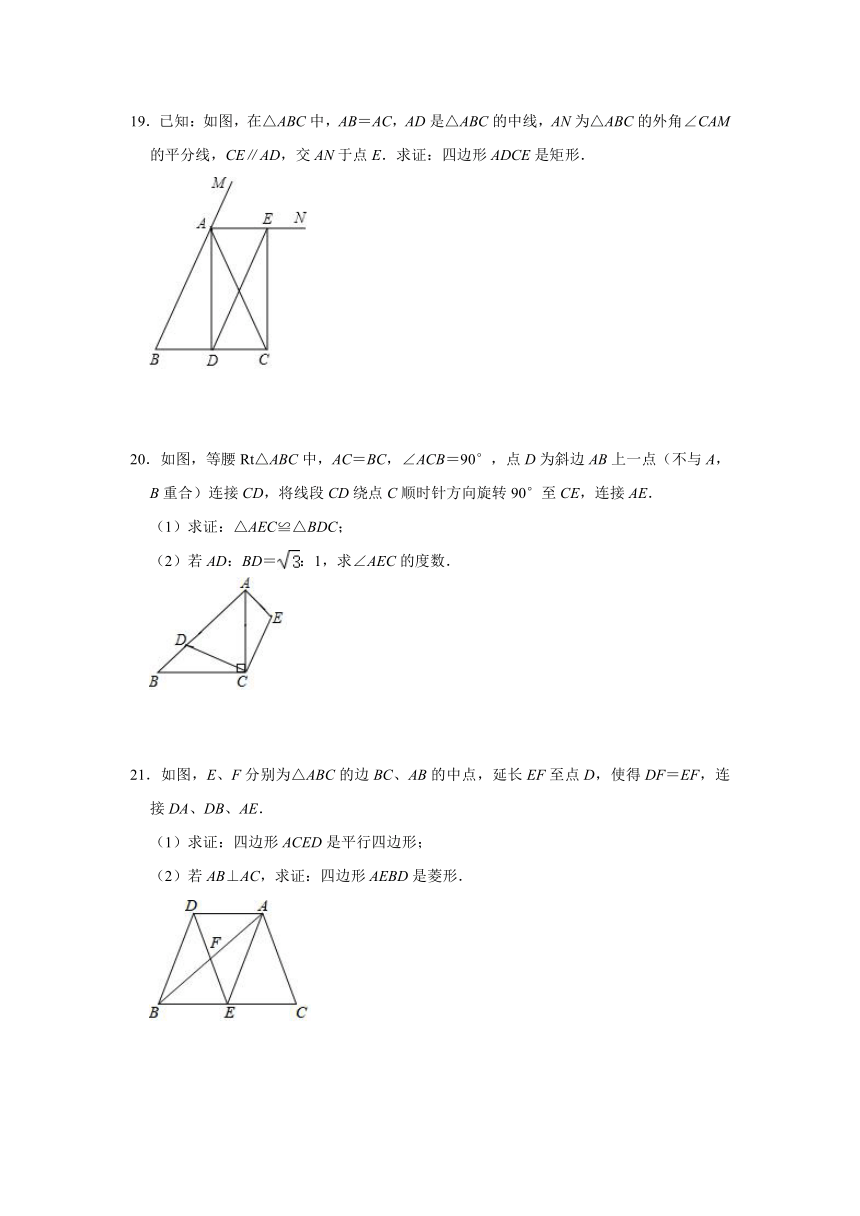
19.已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
20.如图,等腰Rt△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点(不与A,B重合)连接CD,将线段CD绕点C顺时针方向旋转90°至CE,连接AE.
(1)求证:△AEC≌△BDC;
(2)若AD:BD=:1,求∠AEC的度数.
21.如图,E、F分别为△ABC的边BC、AB的中点,延长EF至点D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ACED是平行四边形;
(2)若AB⊥AC,求证:四边形AEBD是菱形.
22.如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
参考答案
一.选择题(共8小题,每小题3分,满分24分)
1.【解答】解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误.
故选:B.
2.【解答】解:顺时针旋转90°,向右平移.
故选:A.
3.【解答】解:∵在△ABC中,D,E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∵DE=2,
∴BC的长度是:4.
故选:C.
4.【解答】解:A、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,故此选项不合题意;
C、∵AB∥CD,∠B=∠D,∴四边形ABCD是平行四边形,故此选项不合题意;
D、∵AB∥CD,AD=BC,不能得出四边形ABCD是平行四边形,故此选项符合题意;
故选:D.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∴DE=AD﹣AE=8﹣3=5
故选:B.
6.【解答】解:A、错误.有3个角为直角的四边形是矩形.
B、正确.矩形的对角线相等.
C、错误.平行四边形的对角线不一定相等.
D、错误.对角线互相垂直的四边形不一定是菱形.
故选:B.
7.【解答】解:根据作图,AC=BC=OA,
∵OA=OB,
∴OA=OB=BC=AC,
∴四边形OACB是菱形,
∵AB=2cm,四边形OACB的面积为4cm2,
∴AB?OC=×2×OC=4,
解得OC=4cm.
故选:C.
8.【解答】解:∵四边形ABCD为平行四边形,
∴PD∥BQ.
若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.
设运动时间为t.
当0<t<时,AP=t,PD=10﹣t,CQ=4t,BQ=10﹣4t,
∴10﹣t=10﹣4t,
方程无解;
当<t<5时,AP=t,PD=10﹣t,BQ=4t﹣10,
∴10﹣t=4t﹣10,
解得:t=4;
当5<t<时,AP=t,PD=10﹣t,CQ=4t﹣20,BQ=30﹣4t,
∴10﹣t=30﹣4t,
解得:t=;
当<t<10时,AP=t,PD=10﹣t,BQ=4t﹣30,
∴10﹣t=4t﹣30,
解得:t=8.
综上所述:当运动时间为4秒、秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.
故选:C.
二.填空题(共8小题,每小题3分,满分24分)
9.【解答】解:∵点B与点A关于原点对称,
∴点B的坐标为(3,﹣4).
故答案为:(3,﹣4).
10.【解答】解:∵△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,
∴∠DAE=∠BAC=30°.
故答案为30°.
11.【解答】解:∵在?ABCD中,∠A=70°,
∴∠B=180°﹣70°=110°,∠A=∠C=70°.
故答案为:110,70.
12.【解答】解:∵在Rt△ABC中,∠ACB=90°,D是AB的中点,
∴线段CD是斜边AB上的中线;
又∵CD=5cm,
∴AB=2CD=10cm.
故答案是:10.
13.【解答】解:由∠A=∠B=∠C=90°可知四边形ABCD是矩形,根据根据有一组邻边相等或对角线互相垂直的矩形是正方形,得到应该添加的条件为:AB=AD或AC⊥BD等.
故答案为:AB=AD或AC⊥BD等.
14.【解答】解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=1,
∴AC=2OA=2,
∴BC===;
故答案为:.
15.【解答】解:延长CF交AB于点G,
∵AE平分∠BAC,
∴∠GAF=∠CAF,
∵AF垂直CG,
∴∠AFG=∠AFC,
在△AFG和△AFC中,
,
∴△AFG≌△AFC(ASA),
∴AC=AG,GF=CF,
又∵点D是BC中点,
∴DF是△CBG的中位线,
∴DF=BG=(AB﹣AG)=(AB﹣AC)=2.
故答案为:2.
16.【解答】解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故答案为16
三.解答题(共6小题,17-20每小题8分,21-22每小题10分,满分52分)
17.【解答】证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC,
∵AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
18.【解答】解:(1)如图,△A′B′C为所作;
(2)点D的坐标为(3,3)或(﹣8,3)或(﹣5,﹣3).
故答案为(3,3)或(﹣8,3)或(﹣5,﹣3).
19.【解答】证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE∥AD,
∴∠AEC=90°,
∴四边形ADCE为矩形.
20.【解答】解:∵将线段CD绕点C顺时针方向旋转90°至CE,
∴∠ACB=∠DCE=90°,DC=CE,
∴∠BCD=∠ACE
而BC=AC,
∴△ACE≌△BCD(SAS);
(2)连接DE,
∵∠DCE=90°,DC=CE,
∴∠DEC=45°,
由(1)知△ACE≌△BCD,
∴BD=AE,∠B=∠CAE=45°,
∴∠BAE=∠BAC+∠CAE=45°+45°=90°,
∵AD:BD=:1,
∴AD:AE=,
∴∠AED=60°,
∴∠AEC=∠AED+∠DEC=60°+45°=105°.
21.【解答】证明:(1)∵E、F分别为△ABC的边BC、BA的中点,
∴EF∥AC,EF=AC,
∵DF=EF,
∴EF=DE,
∴AC=DE,
∴四边形ACED是平行四边形;
(2)∵四边形ACED是平行四边形,
∴AD∥EC,DE∥AC,
AD=EC,
∵BE=EC,
∴AD=BE,AD∥BE,
∴四边形AEBD是平行四边形,
∵AC⊥AB,AC∥DE,
∴AB⊥ED,
∴四边形AEBD是菱形.
22.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD的中点,
∴DO=BO,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,
∴PD=8﹣t,
(3)∵PB=PD,
∴PB2=PD2,
即AB2+AP2=PD2,
∴62+t2=(8﹣t)2,
解得 t=,
∴当t=时,PB=PD.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
