18.1 勾股定理课件 (共24张PPT)
文档属性
| 名称 | 18.1 勾股定理课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
18.1 勾股定理
沪科版 八年级下
新知导入
小故事:有一次,法国数学家毕达哥拉斯去他老朋友家做客,看到他朋友家地砖铺成的地面(如图),回家后,他想:正方形A、B、C的面积之间会不会有什么样的数量关系呢?同学们,你们是怎么想的呢?
新知讲解
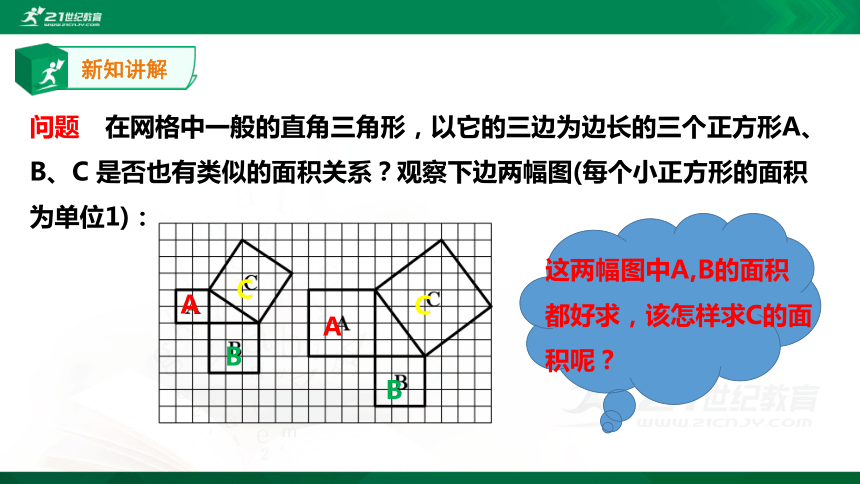
问题 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
A
B
C
A
B
C
新知讲解
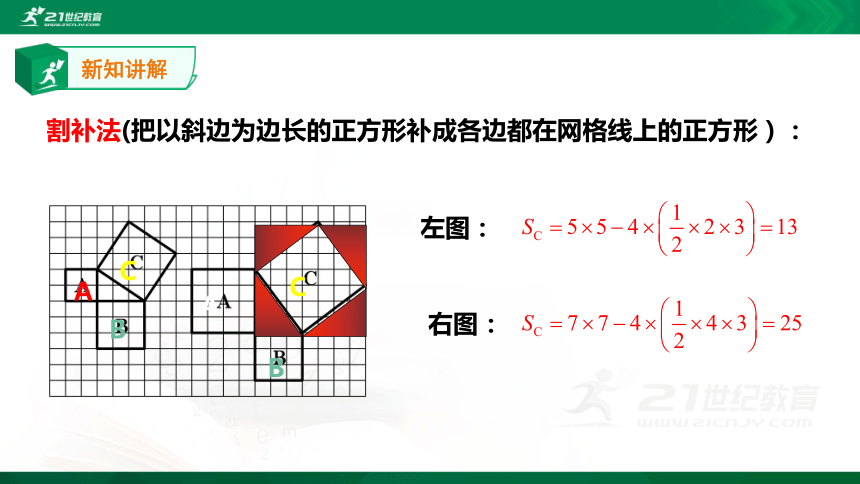
割补法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
A
B
C
C
A
B
新知讲解
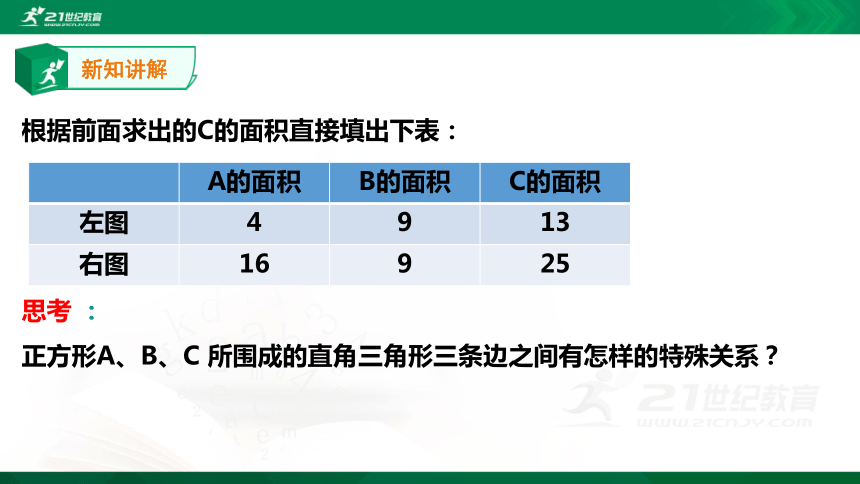
根据前面求出的C的面积直接填出下表:
思考 :
正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
新知讲解
猜想: 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
新知讲解
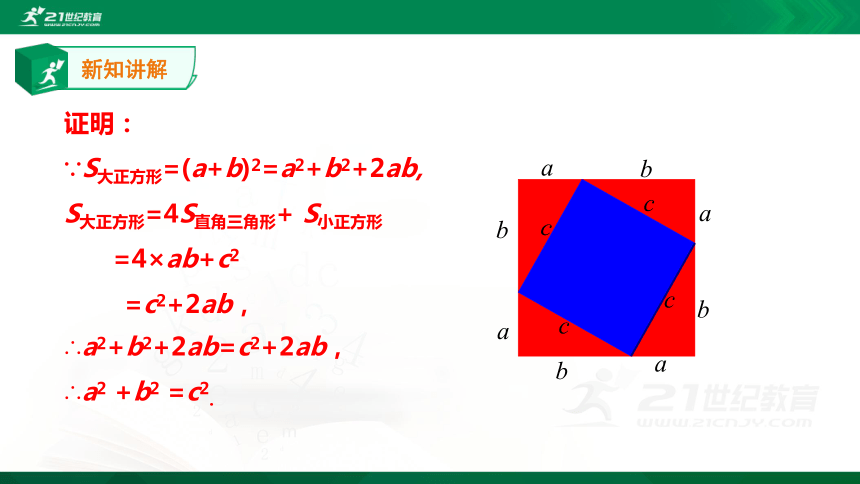
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4×ab+c2
=c2+2ab,
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
新知讲解
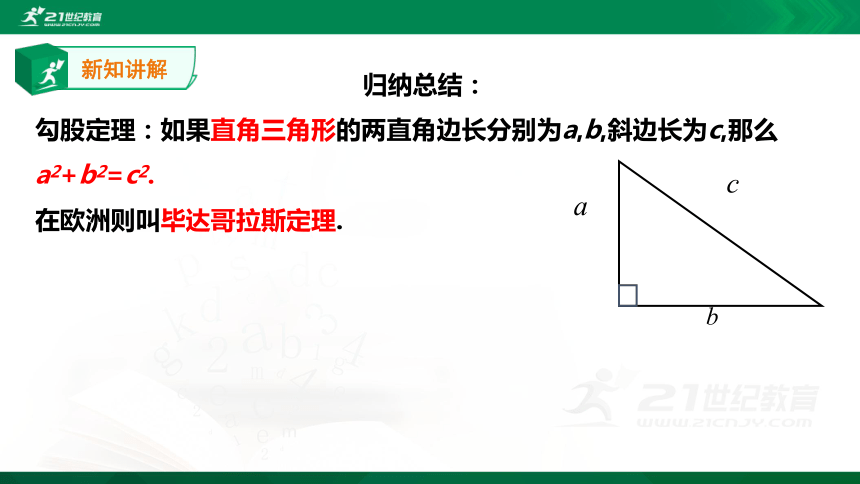
归纳总结:
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
在欧洲则叫毕达哥拉斯定理.
新知讲解
例1.在?ABC中,∠C=900,AB=c, BC=a, AC=b.
(1)a=6,b=8,求c
(2)a=8,c=17,求b
解:(1)根据勾股定理:c2=a2+b2=62+82=100
又∵c>0,∴c=10
(2)根据勾股定理:b2=c2-a2=172-82=225
又∵b>0,∴b=15
新知讲解
例2.已知:如图,在Rt△ABC中,两条直角边AC=5,BC=12.求斜边上的高CD的长.
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=52+122=169,
又∵AB>0,∴AB=13.
S△ABC= AC*BC= AB*CD,
∴
新知讲解
例3.如图,A市气象站测得台风中心在A市正东方向200km的B处,以
km/h的速度向北偏西600的BF方向移动,距台风中心120km范围
内是受台风影响的区域.
(1)A市是否受台风影响?写出你的结论并给予说明;
(2)如果A市受台风影响,
那么受台风影响的时间有多长?
新知讲解
解:(1)A市受台风影响,理由如下:
过点A作AC⊥BF于C,
由题意得:∠ABC=300,AB=200km,则AC= AB=100km.
∵100< 120,∴A市会受到台风的影响.
(2)以A为圆心,120km为半径作弧交BF于C1,C2两点
连接AC1,AC2.
∵AC⊥BF, ∴ C1C2=2C1C.
在Rt△ACC1中,
新知讲解
C1C2=1202-1002=4400
又∵C1C>0,∴C1C= km
∴C1C2= km
∴A市受台风影响的时间为
÷ =8(h).
答:A市受台风影响的时间为8h.
课堂练习
1.如图,在Rt△ABC中,∠C=900,若AC=3,BC=4,求AB.
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=32+42=25,
又∵AB>0,∴AB=5.
课堂练习
2.一棵树在距地面1米处折断,树尖A恰好碰到地面,经过测量AC=2米,则树高为( )
A. 米 B. 米 C. 米 D.3米
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=22+12=5,
又∵AB>0,∴AB= .
则树高为 ( +1)米,故选C
C
课堂练习
3.如图,在Rt△ABC中,它的两边长分别为3和4,求第三边的长.
解:本题有两种情况
(1)如果3和4是两条直角边,那么第三边则为斜边.
在Rt△ABC中,根据勾股定理:不妨设AC=3,BC=4,
∴AB2=AC2+BC2=32+42=25,
又∵AB>0,∴AB=5.
课堂练习
(2)如果3和4是一条直角边,一条斜边,那么第三边则为直角边.
不妨设AC=3,AB=4,
在Rt△ABC中,根据勾股定理:
∴BC2=AB2-AC2=42-32=7,
又∵BC>0,∴BC= .
答:第三边长为
拓展提高
4.如图,圆柱底面圆周长为6㎝,AC是底面圆的直径,高BC=6㎝,点P是母线BC上一点且PC=2/3BC,你能求出一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离吗?
解:把圆柱沿着A--C--P--B展开得到下图:
A
C
P
拓展提高
∵圆柱底面圆周长为6㎝
∴由题意得AC=3㎝
∵BC=6㎝
∴PC=2/3BC= ×6=4㎝
在Rt△ACP中,根据勾股定理:
AP2=AC2+BP2=32+42=25,
又∵AP>0,∴AP=5 .
∴蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离5㎝
中考链接
5.(吉林 中考)如图,每个小正方形的边长为1,△ABC的
三边a,b,c的大小关系式为( )
A. aC.c
A
B
C
b
a
c
c
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
又叫毕达哥拉斯定理.
板书设计
18.1 勾股定理
1.勾股定理
2.例1... 例2... 例3...
作业布置
课本 P57 习题18.1
第2,5,6,7题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.1 勾股定理
沪科版 八年级下
新知导入
小故事:有一次,法国数学家毕达哥拉斯去他老朋友家做客,看到他朋友家地砖铺成的地面(如图),回家后,他想:正方形A、B、C的面积之间会不会有什么样的数量关系呢?同学们,你们是怎么想的呢?
新知讲解
问题 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
A
B
C
A
B
C
新知讲解
割补法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
A
B
C
C
A
B
新知讲解
根据前面求出的C的面积直接填出下表:
思考 :
正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
新知讲解
猜想: 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
新知讲解
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4×ab+c2
=c2+2ab,
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
新知讲解
归纳总结:
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
在欧洲则叫毕达哥拉斯定理.
新知讲解
例1.在?ABC中,∠C=900,AB=c, BC=a, AC=b.
(1)a=6,b=8,求c
(2)a=8,c=17,求b
解:(1)根据勾股定理:c2=a2+b2=62+82=100
又∵c>0,∴c=10
(2)根据勾股定理:b2=c2-a2=172-82=225
又∵b>0,∴b=15
新知讲解
例2.已知:如图,在Rt△ABC中,两条直角边AC=5,BC=12.求斜边上的高CD的长.
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=52+122=169,
又∵AB>0,∴AB=13.
S△ABC= AC*BC= AB*CD,
∴
新知讲解
例3.如图,A市气象站测得台风中心在A市正东方向200km的B处,以
km/h的速度向北偏西600的BF方向移动,距台风中心120km范围
内是受台风影响的区域.
(1)A市是否受台风影响?写出你的结论并给予说明;
(2)如果A市受台风影响,
那么受台风影响的时间有多长?
新知讲解
解:(1)A市受台风影响,理由如下:
过点A作AC⊥BF于C,
由题意得:∠ABC=300,AB=200km,则AC= AB=100km.
∵100< 120,∴A市会受到台风的影响.
(2)以A为圆心,120km为半径作弧交BF于C1,C2两点
连接AC1,AC2.
∵AC⊥BF, ∴ C1C2=2C1C.
在Rt△ACC1中,
新知讲解
C1C2=1202-1002=4400
又∵C1C>0,∴C1C= km
∴C1C2= km
∴A市受台风影响的时间为
÷ =8(h).
答:A市受台风影响的时间为8h.
课堂练习
1.如图,在Rt△ABC中,∠C=900,若AC=3,BC=4,求AB.
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=32+42=25,
又∵AB>0,∴AB=5.
课堂练习
2.一棵树在距地面1米处折断,树尖A恰好碰到地面,经过测量AC=2米,则树高为( )
A. 米 B. 米 C. 米 D.3米
解:在Rt△ABC中,根据勾股定理:
AB2=AC2+BC2=22+12=5,
又∵AB>0,∴AB= .
则树高为 ( +1)米,故选C
C
课堂练习
3.如图,在Rt△ABC中,它的两边长分别为3和4,求第三边的长.
解:本题有两种情况
(1)如果3和4是两条直角边,那么第三边则为斜边.
在Rt△ABC中,根据勾股定理:不妨设AC=3,BC=4,
∴AB2=AC2+BC2=32+42=25,
又∵AB>0,∴AB=5.
课堂练习
(2)如果3和4是一条直角边,一条斜边,那么第三边则为直角边.
不妨设AC=3,AB=4,
在Rt△ABC中,根据勾股定理:
∴BC2=AB2-AC2=42-32=7,
又∵BC>0,∴BC= .
答:第三边长为
拓展提高
4.如图,圆柱底面圆周长为6㎝,AC是底面圆的直径,高BC=6㎝,点P是母线BC上一点且PC=2/3BC,你能求出一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离吗?
解:把圆柱沿着A--C--P--B展开得到下图:
A
C
P
拓展提高
∵圆柱底面圆周长为6㎝
∴由题意得AC=3㎝
∵BC=6㎝
∴PC=2/3BC= ×6=4㎝
在Rt△ACP中,根据勾股定理:
AP2=AC2+BP2=32+42=25,
又∵AP>0,∴AP=5 .
∴蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离5㎝
中考链接
5.(吉林 中考)如图,每个小正方形的边长为1,△ABC的
三边a,b,c的大小关系式为( )
A. a
A
B
C
b
a
c
c
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
又叫毕达哥拉斯定理.
板书设计
18.1 勾股定理
1.勾股定理
2.例1... 例2... 例3...
作业布置
课本 P57 习题18.1
第2,5,6,7题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
