19.1.2 函数的三种表示方法第2课时课课练(含答案)
文档属性
| 名称 | 19.1.2 函数的三种表示方法第2课时课课练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 22:05:55 | ||
图片预览


文档简介
人教版数学八年级下册﹒课课练
第十九章 一次函数
19.1 函数
19.1.2 函数的图象
第2课时 函数的三种表示方法
一、选择题
1.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数解析式是( )
A.y=0.05x B.y=5x C.y=100x D.y=0.05x+100
2.直角三角形中一个锐角的度数y与另一个锐角的度数x的函数解析式为( )
A.y=180°-x(0°C.y=180°-x(0°≤x≤90°) D.y=90°-x(0°≤x≤90°)
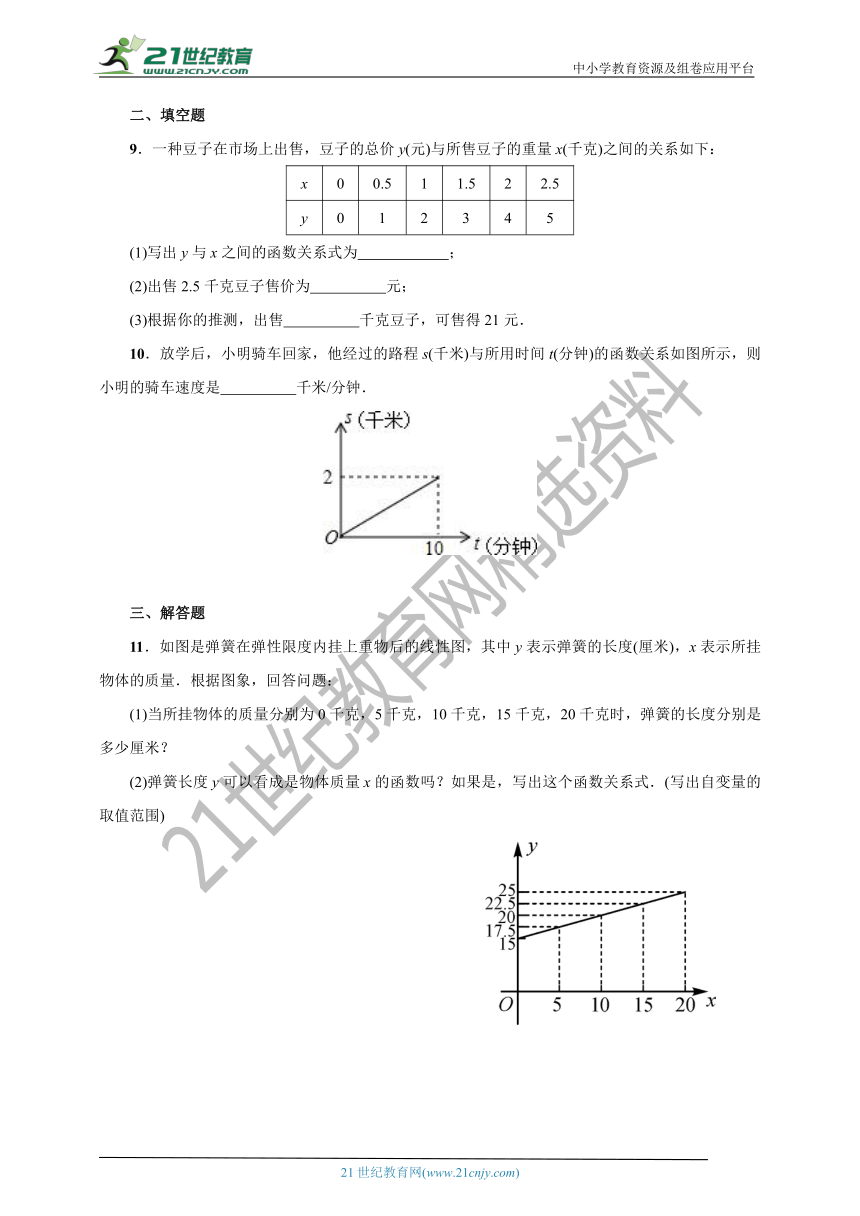
3.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( )
A.y= B.y=-2x+24
C.y=2x-24 D.y=x-12
4.已知汽车油箱内有油30 L,每行驶100 km耗油10 L,则汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的函数解析式是( )
A.Q=30- B.Q=30+
C.Q=30- D.Q=30+
5.弹簧挂上物体后会伸长,测得一根弹簧的长度y(cm)与所挂物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法中,不正确的是( )
A.x是自变量,y是x的函数
B.弹簧不挂重物时长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为13.5 cm
6.下面的表格列出了一个实验的统计数据,表示将皮球从高h处落下,弹跳高度m与下降高度h的关系.
h
50
80
100
150
m
25
40
50
75
则m关于h的函数解析式为( )
A.m=h2 B.m=2h C.m= D.m=h+25
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
A B C D
8.为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:①若每户居民每月用电量不超过100度,则按0.60元/度计算;②若每户居民每月用电量超过100度,则超过部分按0.8元/度计算(未超过部分仍按每度电0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
A B C D
二、填空题
9.一种豆子在市场上出售,豆子的总价y(元)与所售豆子的重量x(千克)之间的关系如下:
x
0
0.5
1
1.5
2
2.5
y
0
1
2
3
4
5
(1)写出y与x之间的函数关系式为 ;
(2)出售2.5千克豆子售价为 元;
(3)根据你的推测,出售 千克豆子,可售得21元.
10.放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
三、解答题
11.如图是弹簧在弹性限度内挂上重物后的线性图,其中y表示弹簧的长度(厘米),x表示所挂物体的质量.根据图象,回答问题:
(1)当所挂物体的质量分别为0千克,5千克,10千克,15千克,20千克时,弹簧的长度分别是多少厘米?
(2)弹簧长度y可以看成是物体质量x的函数吗?如果是,写出这个函数关系式.(写出自变量的取值范围)
12.某校办工厂年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的函数解析式,并画出函数图象;
(2)估计5年后该工厂的产值.
13.一根蜡烛长20 cm,蜡烛的燃烧速度是5 cm/s.
(1)写出蜡烛的剩余长度h与燃烧时间t之间的函数关系式;
(2)画出这个函数的图象.
14.一根合金棒在不同的温度下,其长度也不同,合金棒的长度和温度之间有如下关系:
温度(℃)
…
-5
0
5
10
15
…
长度(cm)
…
9.995
10
10.005
10.01
10.015
…
(1)如果合金棒的长度大于10.05 cm小于10.15 cm,根据表中的数据推测,此时的温度应在什么范围内?
(2)假设温度为x ℃时,合金棒的长度为y cm,根据表中数据写出y与x之间的关系式;
(3)当温度为-20 ℃或100 ℃,分别推测合金棒的长度.
15.已知点P(x,y)是第一象限内的点,且x+y=8,点A的坐标为(10,0).设△OAP的面积为S.
(1)求S与x之间的函数解析式,并写出自变量的取值范围;
(2)画出函数图象.
参 考 答 案
1. B 2. B 3. A 4. C 5. B 6. C 7. D 8. C
9. (1)y=2x (2)5 (3)10.5
10. 0.2
11. 解:(1)15,17.5,20,22.5,25.
(2)可以,y=15+0.5x(0≤x≤20).
12. 解:(1)y=15+2x(x≥0),图象如下:
(2)当x=5时,y=15+2×5=25. ∴估计5年后该工厂的产值为25万元.
13. 解:(1)h=20-5t(0≤t≤4).
(2)列表:
t
0
1
2
3
4
h
20
15
10
5
0
描点、连线,如图.
14. 解:(1) 从表格上可知温度每升高1 ℃合金棒的长度就增加0.001 cm,∴如果合金棒的长度大于10.05 cm小于10.15 cm,根据表中的数据推测,此时的温度应在50 ~150 ℃.
(2)y=0.001x+10.
(3)当x=-20时,y=0.001×(-20)+10=9.98;当x=100时,y=0.001×100+10=10.1.
15. 解:(1)∵P(x,y)在第一象限内,∴x>0,y>0. ∵x+y=8,∴y=8-x. ∴S=OA·y=×10×(8-x),即S=-5x+40. x的取值范围是0(2)图象如图.
第十九章 一次函数
19.1 函数
19.1.2 函数的图象
第2课时 函数的三种表示方法
一、选择题
1.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数解析式是( )
A.y=0.05x B.y=5x C.y=100x D.y=0.05x+100
2.直角三角形中一个锐角的度数y与另一个锐角的度数x的函数解析式为( )
A.y=180°-x(0°
3.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( )
A.y= B.y=-2x+24
C.y=2x-24 D.y=x-12
4.已知汽车油箱内有油30 L,每行驶100 km耗油10 L,则汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的函数解析式是( )
A.Q=30- B.Q=30+
C.Q=30- D.Q=30+
5.弹簧挂上物体后会伸长,测得一根弹簧的长度y(cm)与所挂物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法中,不正确的是( )
A.x是自变量,y是x的函数
B.弹簧不挂重物时长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为13.5 cm
6.下面的表格列出了一个实验的统计数据,表示将皮球从高h处落下,弹跳高度m与下降高度h的关系.
h
50
80
100
150
m
25
40
50
75
则m关于h的函数解析式为( )
A.m=h2 B.m=2h C.m= D.m=h+25
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
A B C D
8.为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:①若每户居民每月用电量不超过100度,则按0.60元/度计算;②若每户居民每月用电量超过100度,则超过部分按0.8元/度计算(未超过部分仍按每度电0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
A B C D
二、填空题
9.一种豆子在市场上出售,豆子的总价y(元)与所售豆子的重量x(千克)之间的关系如下:
x
0
0.5
1
1.5
2
2.5
y
0
1
2
3
4
5
(1)写出y与x之间的函数关系式为 ;
(2)出售2.5千克豆子售价为 元;
(3)根据你的推测,出售 千克豆子,可售得21元.
10.放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
三、解答题
11.如图是弹簧在弹性限度内挂上重物后的线性图,其中y表示弹簧的长度(厘米),x表示所挂物体的质量.根据图象,回答问题:
(1)当所挂物体的质量分别为0千克,5千克,10千克,15千克,20千克时,弹簧的长度分别是多少厘米?
(2)弹簧长度y可以看成是物体质量x的函数吗?如果是,写出这个函数关系式.(写出自变量的取值范围)
12.某校办工厂年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的函数解析式,并画出函数图象;
(2)估计5年后该工厂的产值.
13.一根蜡烛长20 cm,蜡烛的燃烧速度是5 cm/s.
(1)写出蜡烛的剩余长度h与燃烧时间t之间的函数关系式;
(2)画出这个函数的图象.
14.一根合金棒在不同的温度下,其长度也不同,合金棒的长度和温度之间有如下关系:
温度(℃)
…
-5
0
5
10
15
…
长度(cm)
…
9.995
10
10.005
10.01
10.015
…
(1)如果合金棒的长度大于10.05 cm小于10.15 cm,根据表中的数据推测,此时的温度应在什么范围内?
(2)假设温度为x ℃时,合金棒的长度为y cm,根据表中数据写出y与x之间的关系式;
(3)当温度为-20 ℃或100 ℃,分别推测合金棒的长度.
15.已知点P(x,y)是第一象限内的点,且x+y=8,点A的坐标为(10,0).设△OAP的面积为S.
(1)求S与x之间的函数解析式,并写出自变量的取值范围;
(2)画出函数图象.
参 考 答 案
1. B 2. B 3. A 4. C 5. B 6. C 7. D 8. C
9. (1)y=2x (2)5 (3)10.5
10. 0.2
11. 解:(1)15,17.5,20,22.5,25.
(2)可以,y=15+0.5x(0≤x≤20).
12. 解:(1)y=15+2x(x≥0),图象如下:
(2)当x=5时,y=15+2×5=25. ∴估计5年后该工厂的产值为25万元.
13. 解:(1)h=20-5t(0≤t≤4).
(2)列表:
t
0
1
2
3
4
h
20
15
10
5
0
描点、连线,如图.
14. 解:(1) 从表格上可知温度每升高1 ℃合金棒的长度就增加0.001 cm,∴如果合金棒的长度大于10.05 cm小于10.15 cm,根据表中的数据推测,此时的温度应在50 ~150 ℃.
(2)y=0.001x+10.
(3)当x=-20时,y=0.001×(-20)+10=9.98;当x=100时,y=0.001×100+10=10.1.
15. 解:(1)∵P(x,y)在第一象限内,∴x>0,y>0. ∵x+y=8,∴y=8-x. ∴S=OA·y=×10×(8-x),即S=-5x+40. x的取值范围是0
