沪科版七年级下册数学:8.2.3 多项式与多项式相乘 课件 (共15张PPT)
文档属性
| 名称 | 沪科版七年级下册数学:8.2.3 多项式与多项式相乘 课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-27 10:51:41 | ||
图片预览






文档简介
课件15张PPT。复习、导入一.如何计算单项式与单项式相乘? 单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。如:复习、导入二.如何计算单项式与多项式相乘? 单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加。如:= aX+bX (a+b) ·X 当 X=m+n 时, (a+b)X 怎么计算?
当 X=m+n 时, (a+b)X =(a+b)(m+n)
复习、导入8.2.3 多项式与多项式相乘 讨论、探究 当 X=m+n 时, (a+b)X 怎么计算?
当 X=m+n 时, (a+b)X =(a+b)(m+n)
(a+b)X=aX+bX 讨论、探究
由上一题知 (a+b)X=aX+bX
于是,当 X=m+n 时
(a+b)X=(a+b)(m+n)
=a(m+n)+b(m+n)
=am+an+bm+bn
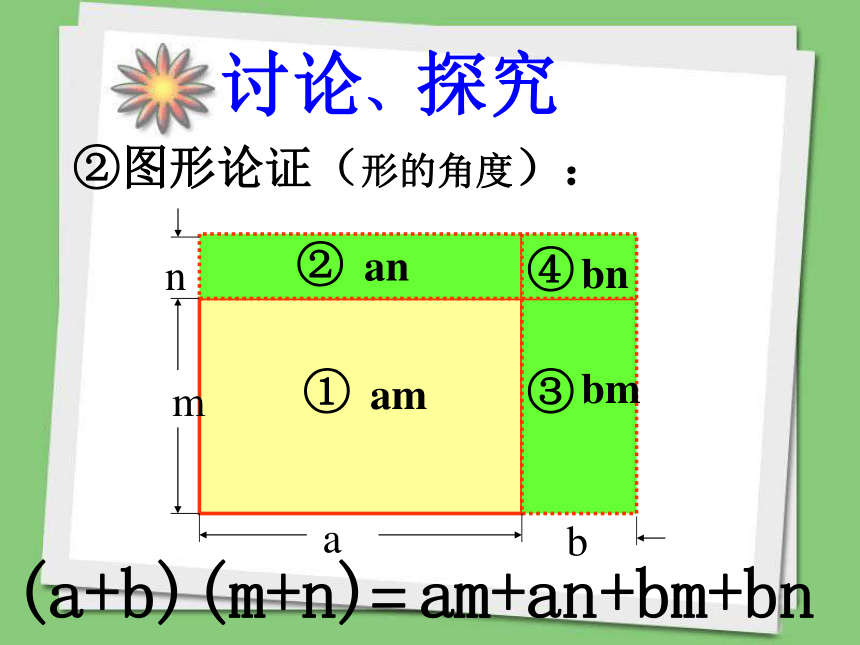
即 (a+b)(m+n)=am+an+bm+bn ①换元代入(数的角度): 讨论、探究②图形论证(形的角度):④②①③(a+b)(m+n)ambmanbnam+an+bm+bn=1234(a+b)(m+n)=am+an+bm+bn 观察、发现(a+b)(m+n)=am1234 an bm bn 观察、发现+++归纳、总结
多项式与多项式相乘, 先用一个多项式的每一项与另一个多项式的每一项相乘, 再把所得的积相加.
多项式与多项式的乘法法则:提示:
在运算还未熟练时,算之前可以先把多项式包含的每一项拆分出来.
﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍ 例 计算: (1) (x+2y)(5a+3b) ;拆分成多个单项式:(x,2y)(5a,3b)按法则算得:x·5a , x·3b , 2y·5a , 2y·3b积相加得:x·5a+x·3b+2y·5a+2y·3b解:(x+2y)(5a+3b) =x ·5a +x ·3b +2y ·5a +2y ·3b=5ax+3bx+10ay+6by示范、应用﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍
(2) (-2x–3)(x-4) ;拆分成多个单项式:(-2x,-3)(x,-4)按法则算得:-2x·x, -2x·(-4), -3·x , -3×(-4)积相加得:-2x·x+(-2x)·(-4)+(-3)·x
+(-3)×(-4)解:(-2x–3)(x-4)-2x2 +8x –3x +12= -2x2 +5x=+12示范、应用
(1) (2n+6)(n–3)练习、巩固 (2) (3x-y)(3x+y)(3) (x+y)(x2–xy+y2)概括、小结⑴多项式的乘法法则:
⑵计算多项式相乘的一般步骤:
①拆;
②乘;③加。P65 4 (4)(5)(6)
P66 10 (2) 12
课堂、作业
当 X=m+n 时, (a+b)X =(a+b)(m+n)
复习、导入8.2.3 多项式与多项式相乘 讨论、探究 当 X=m+n 时, (a+b)X 怎么计算?
当 X=m+n 时, (a+b)X =(a+b)(m+n)
(a+b)X=aX+bX 讨论、探究
由上一题知 (a+b)X=aX+bX
于是,当 X=m+n 时
(a+b)X=(a+b)(m+n)
=a(m+n)+b(m+n)
=am+an+bm+bn
即 (a+b)(m+n)=am+an+bm+bn ①换元代入(数的角度): 讨论、探究②图形论证(形的角度):④②①③(a+b)(m+n)ambmanbnam+an+bm+bn=1234(a+b)(m+n)=am+an+bm+bn 观察、发现(a+b)(m+n)=am1234 an bm bn 观察、发现+++归纳、总结
多项式与多项式相乘, 先用一个多项式的每一项与另一个多项式的每一项相乘, 再把所得的积相加.
多项式与多项式的乘法法则:提示:
在运算还未熟练时,算之前可以先把多项式包含的每一项拆分出来.
﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍ 例 计算: (1) (x+2y)(5a+3b) ;拆分成多个单项式:(x,2y)(5a,3b)按法则算得:x·5a , x·3b , 2y·5a , 2y·3b积相加得:x·5a+x·3b+2y·5a+2y·3b解:(x+2y)(5a+3b) =x ·5a +x ·3b +2y ·5a +2y ·3b=5ax+3bx+10ay+6by示范、应用﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍
(2) (-2x–3)(x-4) ;拆分成多个单项式:(-2x,-3)(x,-4)按法则算得:-2x·x, -2x·(-4), -3·x , -3×(-4)积相加得:-2x·x+(-2x)·(-4)+(-3)·x
+(-3)×(-4)解:(-2x–3)(x-4)-2x2 +8x –3x +12= -2x2 +5x=+12示范、应用
(1) (2n+6)(n–3)练习、巩固 (2) (3x-y)(3x+y)(3) (x+y)(x2–xy+y2)概括、小结⑴多项式的乘法法则:
⑵计算多项式相乘的一般步骤:
①拆;
②乘;③加。P65 4 (4)(5)(6)
P66 10 (2) 12
课堂、作业
