五年级上册数学试题 -组合图形的面积 沪教版 含答案
文档属性
| 名称 | 五年级上册数学试题 -组合图形的面积 沪教版 含答案 |

|
|
| 格式 | zip | ||
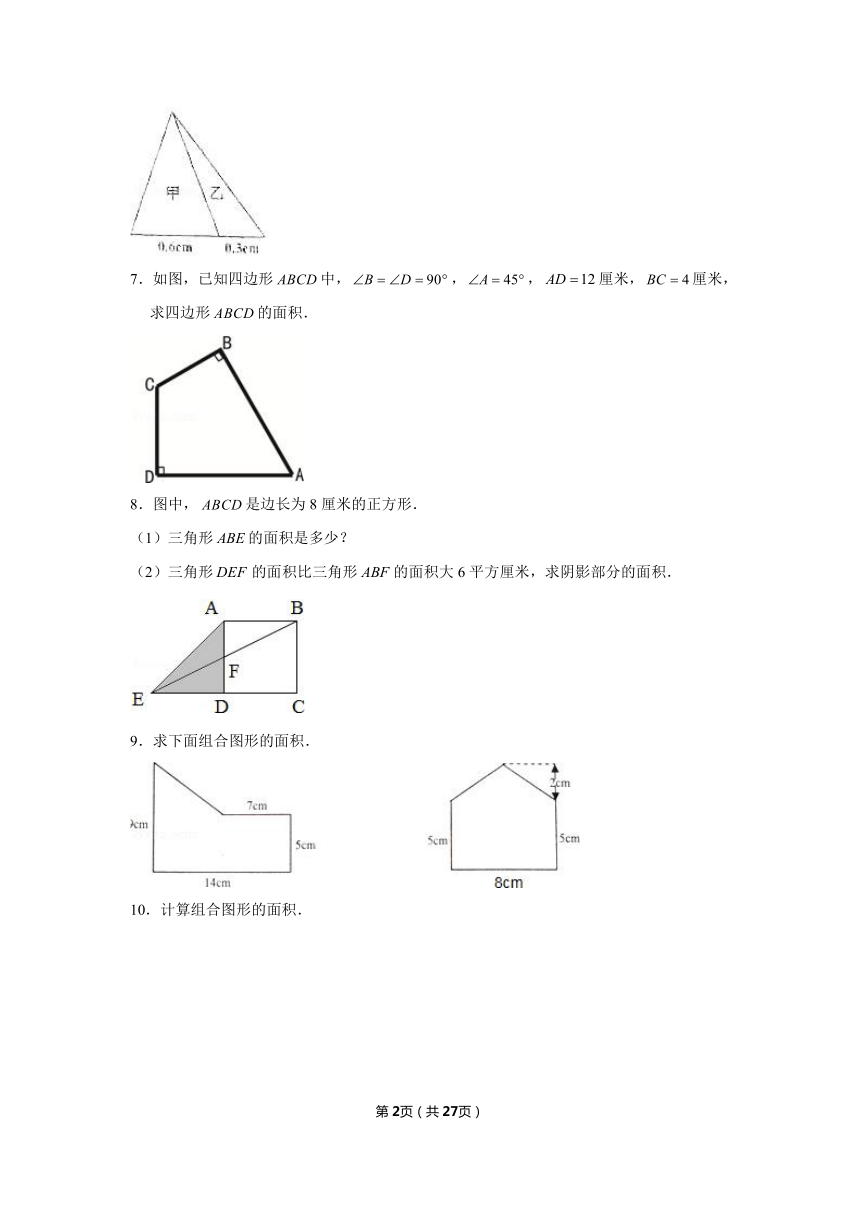
| 文件大小 | 865.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览

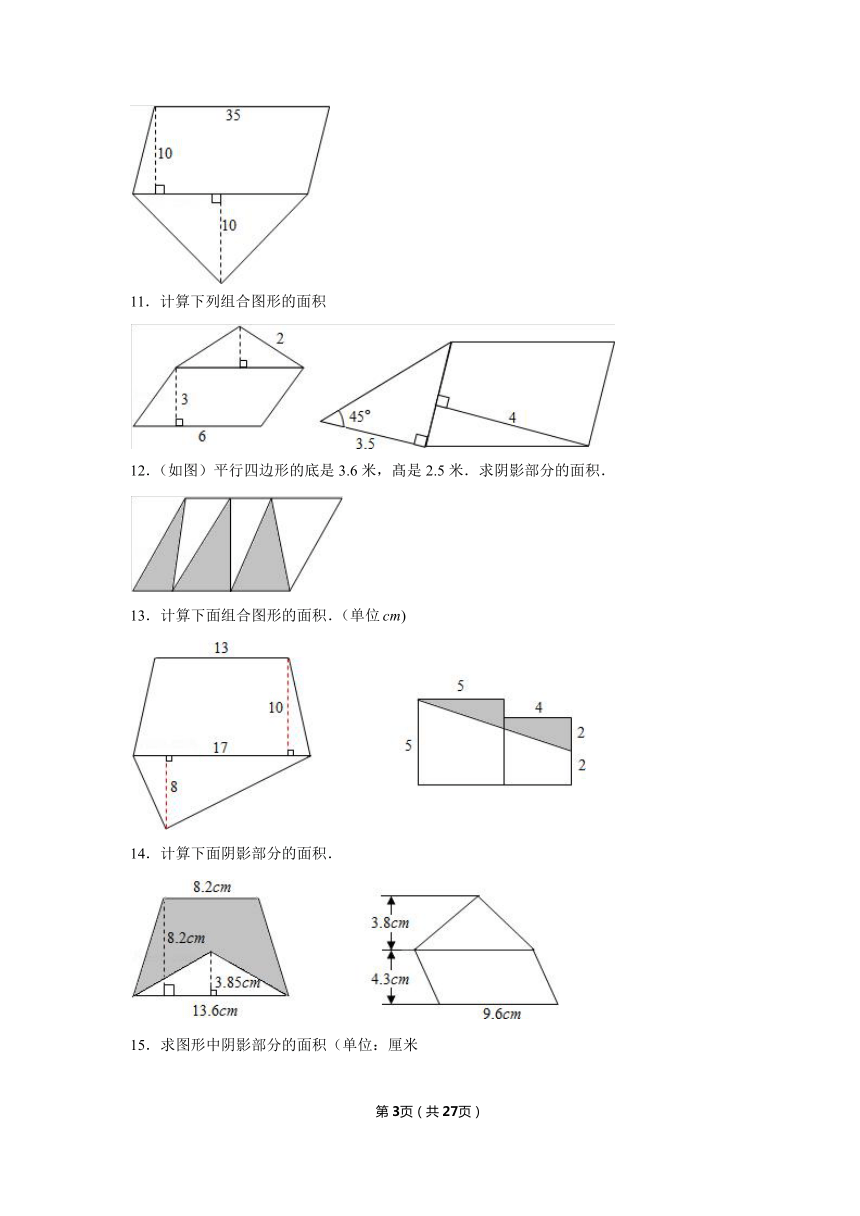
文档简介
沪教版五年级上册《组合图形的面积》2019年同步练习卷
一.组合图形的面积(共40小题)
1.下图中的两个正方形的边长分别为8厘米和5厘米,求阴影部分的面积.
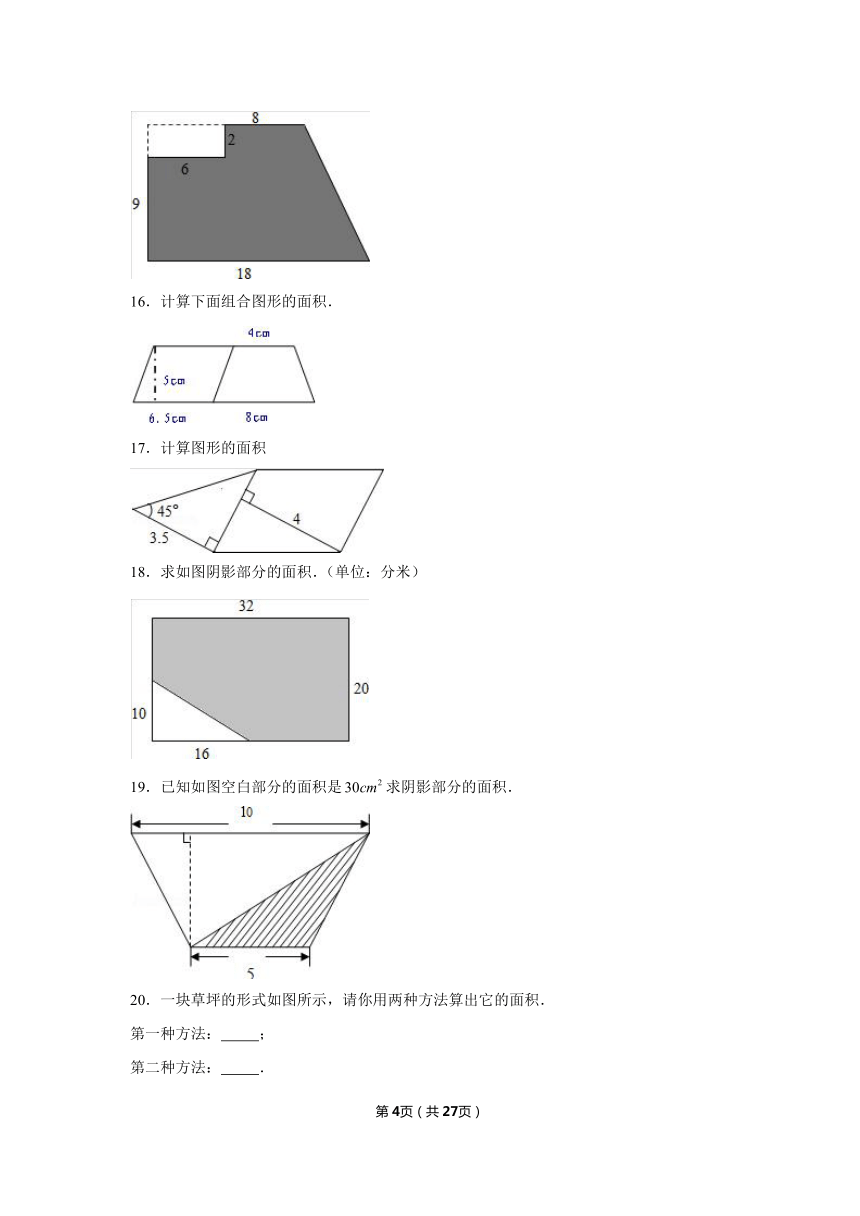
2.北京某四合院子正好是个边长10米的正方形,在院子中央修了一条宽2米的“十字形”的路,如图.这条“十字形”路的面积是多少平方米?
3.求梯形中阴影部分的面积.(单位:厘米)
4.如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.长方形的面积是多少?
5.如图所示,直角梯形的面积为225平方厘米,厘米,厘米,三角形的面积为100平方厘米.阴影部分的面积是多少平方厘米?
6.如图的三角形分成两部分,甲的面积是,乙的面积是 .
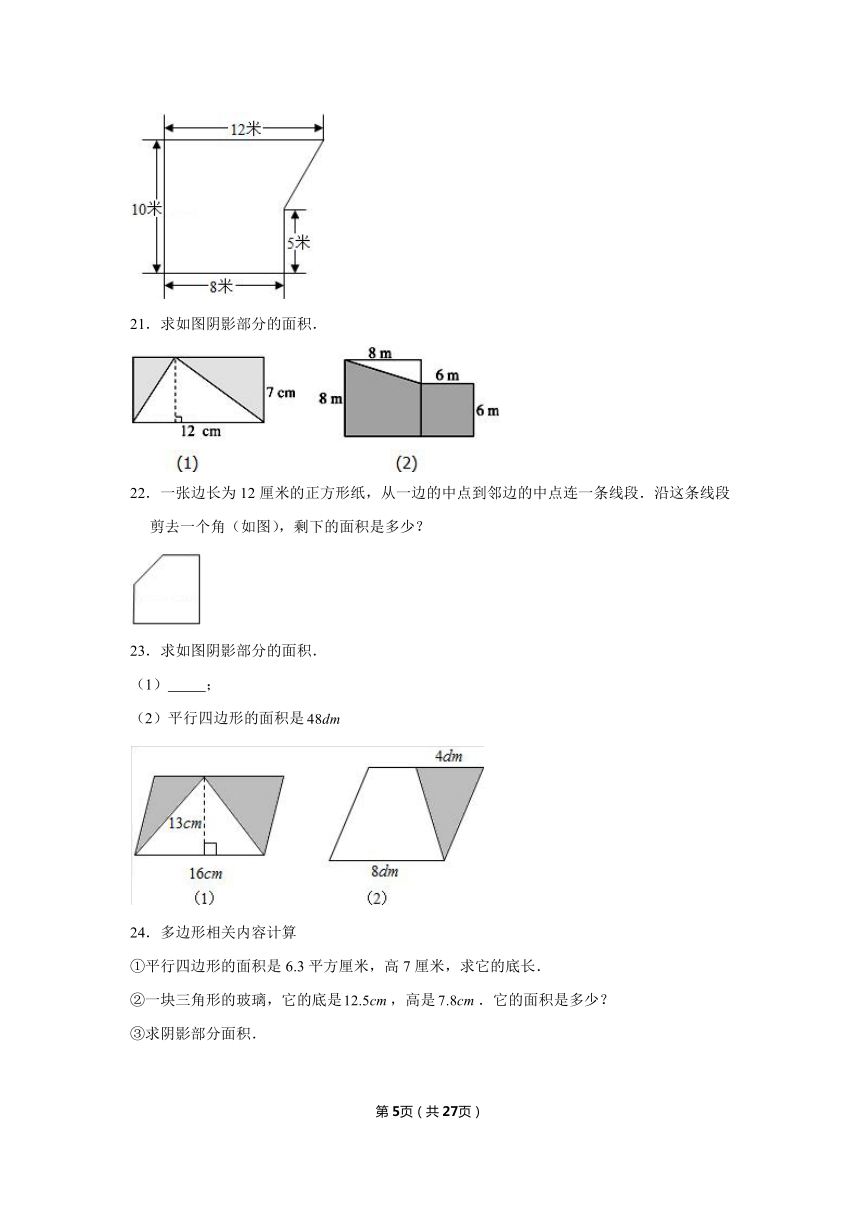
7.如图,已知四边形中,,,厘米,厘米,求四边形的面积.
8.图中,是边长为8厘米的正方形.
(1)三角形的面积是多少?
(2)三角形的面积比三角形的面积大6平方厘米,求阴影部分的面积.
9.求下面组合图形的面积.
10.计算组合图形的面积.
11.计算下列组合图形的面积
12.(如图)平行四边形的底是3.6米,髙是2.5米.求阴影部分的面积.
13.计算下面组合图形的面积.(单位
14.计算下面阴影部分的面积.
15.求图形中阴影部分的面积(单位:厘米
16.计算下面组合图形的面积.
17.计算图形的面积
18.求如图阴影部分的面积.(单位:分米)
19.已知如图空白部分的面积是求阴影部分的面积.
20.一块草坪的形式如图所示,请你用两种方法算出它的面积.
第一种方法: ;
第二种方法: .
21.求如图阴影部分的面积.
22.一张边长为12厘米的正方形纸,从一边的中点到邻边的中点连一条线段.沿这条线段剪去一个角(如图),剩下的面积是多少?
23.求如图阴影部分的面积.
(1) ;
(2)平行四边形的面积是
24.多边形相关内容计算
①平行四边形的面积是6.3平方厘米,高7厘米,求它的底长.
②一块三角形的玻璃,它的底是,高是.它的面积是多少?
③求阴影部分面积.
25.计算图中阴影部分的面积.
26.如图,两个正方形的边长分别为6厘米和4厘米,求阴影部分的面积是多少?
27.计算下列图形阴影部分的面积(单位:分米)
28.如图:在梯形中,厘米,厘米,的面积是10平方厘米米,求阴影部分的面积.
29.图中阴影部分的面积是 平方厘米.
30.一个长方形(如图),阴影部分面积是45平方米,这个大长方形的面积是
平方米.
31.如图中,四边形的面积是 .
32.如图,平行四边形的面积是72平方米,那么图中阴影部分的面积是 平方米.
33.如图,长方形中,,,是的中点,,为上任意一点,则阴影部分的总面积是 .
34.在正方形中,切去四个三角形得到一个五边形(如图,其中所标的数表示各线段的长度),线段将五边形分成两个面积相等的部分,那么的长度是 .
35.两个相同的长方形,长为20厘米,宽为9厘米,按如图叠放在一起.这个图形的面积是多少平方厘米?
36.如图(单位:厘米)是两个相同的直角梯形重叠在一起.求阴影部分的面积.
37.如图,把一张长19厘米,宽13厘米的长方形白纸折成右图形壮,厘米,求阴影部分的面积.
38.求如图组合图形的面积.(单位:厘米)
39.一个长方形与一个平行四边形交叠在一起,如图所示.(单位:厘米)
①阴影部分是一个特殊的四边形,它是 形.
②求阴影部分的面积.
40.如图:长方形面积是40平方米,点是一边上的中点,那么两个三角形的总面积是 平方米.
沪教版五年级上册《组合图形的面积》2019年同步练习卷
参考答案与试题解析
一.组合图形的面积(共40小题)
【分析】根据题意,阴影部分的面积等于梯形的面积减去三角形的面积,根据梯形的面积公式和三角形的面积公式进行计算即可得到答案.
【解答】解:如图
梯形的面积为:
,
,
(平方厘米),
三角形的面积为:
,
(平方厘米),
阴影部分的面积为:(平方厘米),
答:阴影部分的面积为52.5平方厘米.
【点评】解答此题的关键是将阴影部分与三角形看作是一个梯形,然后再用梯形的面积减去三角形的面积即可.
【分析】此题可以利用平移,把除路以外的地方利用平移拼成一个新的正方形,其边长即为原正方形的边长减去路宽,然后用原正方形的面积减去新正方形的面积即可得到路的面积.
【解答】解:
(平方米);
答:这条“十字形”路的面积是36平方米.
【点评】本题实质上是利用了转化的思想方法,结合平移,把不规则图形的面积转化为规则图形的面积的和或差来解决.
【分析】根据图意可知,阴影部分的面积等于梯形的面积减去空白三角形的面积,据此代入数据计算即可解答.
【解答】解:
(平方厘米)
答:阴影部分的面积是135平方厘米.
【点评】本题主要考查组合图形的面积,熟练找出阴影部分是由哪几部分的和或差得到的是解答本题的关键.
【分析】如图所示,由题意可知:三角形①、②、③、④应均为等腰直角三角形,且①和③组成1个边长为4厘米的正方形,②和④能组成1个边长为12厘米的正方形,用大正方形的面积分别减去这两个小正方形的面积,就是长方形的面积.
【解答】解:由题意可得:(厘米),
(厘米),
所以长方形的面积是:
,
,
(平方厘米);
答:长方形的面积是96平方厘米.
【点评】解答此题的关键是:利用其他图形的面积和或差求出长方形的面积.
【分析】直角梯形的面积和上、下底已知,则可以利用梯形的面积公式求出的长度,又因三角形的面积和底边已知,则可以求出边上的高的长度,进而可以求出三角形的边上的高,于是即可求出三角形的面积,用梯形的面积分别减去两个空白三角形的面积,就是阴影部分的面积.
【解答】解:如图所示:
的长度:
(厘米);
的长度:
(厘米);
的长度:
(厘米)
三角形的面积:
(平方厘米);
阴影部分的面积:
(平方厘米)
答:阴影部分的面积是100平方厘米.
【点评】此题主要考查梯形和三角形的面积公式的灵活应用.
【分析】观察图得出甲三角形的底是乙三角形底的2倍,两个三角形的高相等,所以乙三角形的面积是甲三角形的面积的一半.
【解答】解:因为甲三角形的底是乙三角形底的2倍,两个三角形的高相等,
所以乙三角形的面积是:(平方厘米),
答:乙的面积是5平方厘米;
故答案为:5.
【点评】关键是根据题意得出高相等的两个三角形,它们的面积比就是底的比.
【分析】如图,
观察图示可知,四边形的面积底和高为12厘米的大等腰直角三角形面积底和高为4厘米的小等腰直角三角形面积,根据三角形面积公式,代入数据,进一步解答即可.
【解答】解:
(平方厘米)
答:四边形的面积是64平方厘米.
【点评】组合图形的面积计算,可以根据几何图形的特征,通过分割、割补、平移、翻折、对称、旋转等方法,化复杂为简单,变组合图形为基本图形的加减组合.
【分析】(1)三角形的底为8厘米,高为8厘米,运用三角形面积公式:,解决问题.
(2)根据题意,三角形比三角形面积大6平方厘米,那么三角形的面积比正方形的面积大6平方厘米,可利用正方形的面积加上6平方厘米就是三角形的的面积,设为厘米,得,解方程求出的长,再利用三角形面积公式求出阴影部分的面积即可.
【解答】解:(1)
(平方厘米)
答:三角形的面积是32平方厘米.
(2)设为厘米,得:
(平方厘米)
答:阴影部分的面积是38平方厘米.
【点评】此题考查了三角形面积公式的灵活运用.第二问:关键在于求得的长度.
【分析】如图所示:将每个图形分割成一个长方形和一个三角形,然后利用长方形和三角形的面积公式即可求解.
【解答】解:
(平方厘米)
答:这个图形的面积是84平方厘米.
(平方厘米)
答:这个图形的面积是48平方厘米.
【点评】解答此题的关键是将图形分割成规则图形,再根据规则图形的面积公式进行解答即可.
【分析】这个图形的面积三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:
答:这个图形的面积是525.
【点评】此题主要考查三角形和平行四边形的面积公式的灵活应用.
【分析】这两个图形的面积都等于三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:(1)
答:这个图形的面积是24.
(2)
答:这个图形的面积是20.125.
【点评】此题主要考查三角形和平行四边形的面积公式的灵活应用.
【分析】观察图形知道,阴影部分的面积就是底是3.6米,髙是2.5米的三角形的面积,利用三角形的面积公式即可解答.
【解答】解:
(平方米)
答:阴影部分的面积是4.5平方米.
【点评】不同的阴影部分的面积就是平行四边形的面积的一半.
【分析】(1)组合图形的面积平行四边形的面积三角形的面积,利用三角形和平行四边形的面积公式即可求解;
(2)组合图形的面积两个正方形面积之和下面梯形的面积,运用正方形和梯形面积公式解答即可.
【解答】解:(1)
(平方厘米)
答:组合图形的面积是218平方厘米.
(2)
(平方厘米)
答:组合图形的面积是9.5平方厘米.
【点评】解答此题的关键是:将图形分割成规则图形,再利用规则图形的面积和或差求解.
【分析】(1)阴影部分的面积梯形的面积空白部分的面积,于是利用梯形的面积公式和三角形的面积公式即可求解.
(2)阴影部分的面积三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是63.2平方厘米.
(2)
(平方厘米)
答:阴影部分的面积是59.52平方厘米.
【点评】此题主要考查梯形、三角形和平行四边形的面积公式的灵活应用.
【分析】阴影部分的面积梯形形的面积长方形的面积,然后根据梯形的面积公式和长方形的面积公式解答即可.
【解答】解:
(平方厘米)
答:阴影部分的面积是105平方厘米.
【点评】本题考查了圆与组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
【分析】根据题意,组合图形的面积平行四边形的面积梯形的面积,运用平行四边形的面积公式:,梯形的面积公式:,计算即可.
【解答】解:
(平方厘米)
答:组合图形的面积为62.5平方厘米.
【点评】此题也可把此组合图形看作梯形,上底为厘米,下底为厘米,运用梯形面积公式列式为:.
【分析】由图意可知:这个图形由一个三角形和一个平行四边形组成,利用三角形和平行四边形的面积公式即可求解.因为三角形是一个等腰直角三角形,因此平行四边形的底为3.5,然后运用三角形和平行四边形的面积公式解答即可.
【解答】解:
答:图形的面积是20.125.
【点评】此题主要考查利用规则图形的面积和求图形的面积,关键求出平行四边形的底的长度.
【分析】阴影部分的面积等于长方形的面积减去空白三角形的面积,利用长方形的面积公式,和三角形的面积公式即可求解.
【解答】解:
(平方分米)
答:阴影部分的面积是560平方分米.
【点评】此题主要考查长方形和三角形的面积公式的灵活应用.
【分析】由三角形的面积公式可得:,据此即可求出空白部分的高,也就等于知道了阴影部分的高,再利用三角形的面积公式即可求解.
【解答】解:
(厘米)
(平方厘米)
答:阴影部分的面积是15平方厘米.
【点评】此题主要考查三角形的面积公式的灵活应用.
【分析】(1)如图所示:这个图形的面积梯形的面积长方形的面积,据此利用长方形和梯形的面积公式即可求解.
(2)这个图形的面积长方形的面积三角形的面积,据此利用三角方形和梯形的面积公式即可求解.
【解答】解:(1)
(平方米)
答:这块草坪的面积是90平方米.
(2)
(平方米)
答:这块草坪的面积是90平方米.
故答案为:,.
【点评】解答此题的关键是:将图形分割成两个规则图形再解答即可.
【分析】(1)影部分的面积长方形的面积空白三角形的面积.据此解答.
(2)阴影部分的面积大方形面积小正方形面积空白三角形面积.据此解答.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是42平方厘米.
(2)
(平方厘米)
答:阴影部分的面积是92平方厘米.
【点评】在求不规则图形的面积时,一般要把不规则图形的面积转化为几个规则图形的面积相加或相减的方法进行计算.
【分析】剩余部分的面积正方形的面积三角形的面积,正方形的边长是12分米,三角形的两条边是分米,根据正方形和三角形的面积进行计算即可.据此解答.
【解答】解:
(平方分米)
答:剩下的面积是126平方分米.
【点评】本题主要考查了学生对正方形和三角形面积公式的掌握.
【分析】(1)平行四边形和空白部分(三角形)等底等高,所以平行四边形的面积就等于三角形的面积的2倍,也就是说阴影部分和空白部分的面积相等,于是利用三角形的面积公式即可求解;
(2)先用平行四边形的面积48平方分米,除以它的底8分米,即可得出平行四边形的高,也就等于知道了阴影部分的高,于是利用三角形的面积公式即可求解.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是104平方厘米.
(2)
(平方分米)
答:阴影部分的面积是12平方分米.
故答案为:104平方厘米.
【点评】此题主要考查平行四边形和三角形的面积公式的灵活应用.
【分析】(1)根据平行四边形的面积公式可得:平行四边形的底面积高,据此计算即可解答问题.
(2)根据三角形的面积公式底高计算出玻璃的面积即可.
(3)阴影部分的面积等于大长方形的面积减去空白部分梯形的面积,据此代入数据计算即可解答.
【解答】解:①(厘米)
答:它的底长是0.9厘米.
②
(平方厘米)
答:它的面积是48.75平方厘米.
③
(平方米)
答:阴影部分面积是17平方米.
【点评】本题主要考查平行四边形、三角形长方形、梯形的面积公式,熟练掌握公式是解答本题的关键.
【分析】阴影部分可看做两个三角形,直接运用三角形面积公式计算出每个三角形的面积,再相加即可.
【解答】解:
答:阴影部分的面积为51.5.
【点评】此题主要考查学生对三角形面积公式的掌握情况.
【分析】要求阴影部分的面积,我们先求出2个正方形的面积,用2个正方形的面积的和减去大正方形面积的一半,再减去大三角形的面积就是阴影部分的面积.
【解答】解:
(平方厘米)
答:图中阴影部分的面积14平方厘米.
【点评】本题运用正方形的面积公式及三角形的面积公式进行计算,考查了学生灵活解决问题的能力.
【分析】(1)用两个正方形的面积和减去直角三角形的面积即可.
(2)用长方形的面积减去梯形的面积即可解答.
【解答】解:(1),
,
(平方分米);
(2),
,
(平方分米).
【点评】本题主要考查了组合图形的面积,解题关键是熟练掌握长方形、正方形、梯形、三角形的面积公式.
【分析】如图所示,空白三角形的面积已知,利用三角形的面积公式即可求出这个三角形的高,也就等于知道了梯形的高,进而利用梯形的面积公式即可求解.
【解答】解:(厘米),
,
,
,
(平方厘米);
(平方厘米);
答:阴影部分的面积是22.5平方厘米.
【点评】此题主要考查三角形和梯形的面积的计算方法,关键是先求出三角形的高.
【分析】由于平行四边形里的两个三角形是等高的,它们的底加起来是平行四边形的长30,高是平行四边形的高12,所以两个三角形面积之和等于平行四方形面积的一半,根据平行四边形的面积公式,进行解答即可.
【解答】解:
(平方厘米)
答:阴影部分的面积是180平方厘米.
故答案为:180.
【点评】此题考查了三角形面积和平行四边形面积的求法,只要找出它们之间的数量关系进行解答即可.
【分析】依据三角形的面积是与其等底等高的长方形面积的一半,即可进行解答.
【解答】解:(平方米);
答:这个大长方形的面积是90平方米.
故答案为:90.
【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形(长方形)面积的一半.
【分析】如图,延长、,交点为,则得出一个大等腰直角三角形,并画出斜边上的高线,则厘米,所以大等腰直角三角形的面积等于平方厘米,则这个四边形的面积等于大等腰直角三角形的面积,减去上面的直角边长为4厘米的小等腰直角三角形的面积,据此计算即可解答问题.
【解答】解:根据题干分析可得:延长、,交点为,则得出一个大等腰直角三角形,并画出斜边上的高线,则厘米,
(平方厘米)
答:四边形的面积是41平方厘米.
故答案为:41.
【点评】解答此题的关键是画出合适的辅助线,利用等腰直角三角形的性质和三角形的面积公式计算即可解答问题.
【分析】空白三角形与平行四边形等底等高,所以三角形的面积是平行四边形的面积的一半,那么阴影部分的面积是平行四边形的面积的一半,用平行四边形的面积除以2即可求出阴影部分的面积.
【解答】解:(平方米)
答:图中阴影部分的面积是 36平方米.
故答案为:36.
【点评】解决本题关键是明确:三角形的面积是和它等底等高的平行四边形面积的一半.
【分析】我们做一条辅助线即连接,与的高的长度是,因为,所以这两个三角形的面积的和较容易解答了,的面积比较容易解得.
【解答】解:连接,
厘米,
阴影部分的面积是:
,
,
,
,
,
,
(平方厘米);
故答案为:324.
【点评】本题是一道复杂的组合图形,考查了学生对三角形的面积公式的运用情况.
【分析】由题意可知:正方形的面积减去4个三角形的面积,就能得到中间五边形的面积,进而求出四边形的面积,于是即可求得梯形的面积,从而利用梯形的面积公式即可求出的长度,进而得出的长度.
【解答】解:四边形的面积为:
,
,
,
,
;
设的长度为,
则,
,
,
,
;
答:的长度是3.25.
故答案为:3.25.
【点评】解答此题的关键是先求出中间五边形的面积,进而得到梯形的面积,问题即可得解.
【分析】这个图形面积比原来减少了重叠部分的边长为9厘米的正方形的面积,然后根据长方形的面积长宽,求出一个长方形的面积,再乘2,求出两个长方形的面积,然根据正方形的面积边长边长求出正方形的面积,再作差.
【解答】解:
(平方厘米)
答:这个图形的面积是279平方厘米.
【点评】解决本题注意观察图,找清楚这个图形的组成部分,再利用长方形和正方形的面积公式求解.
【分析】由题意可知:阴影部分的面积就等于空白的较大一点的梯形的面积,这个梯形的下底和高已知,上底可以求出,从而可以求其面积,也就求得了阴影部分的面积.
【解答】解:,
,
,
,
(平方厘米);
答:阴影部分的面积是140平方厘米.
【点评】解答此题的关键是明白:阴影部分的面积就等于空白的较大一点的梯形的面积.
【分析】如图所示,阴影部分的面积梯形的面积折过来的部分的面积,又因梯形的上底、下底和高分别为5.5厘米、13厘米和19厘米,折过来的部分的两条直角边分别为厘米、19厘米,从而利用梯形和三角形的面积公式即可求解.
【解答】解:
(平方厘米)
答:阴影部分的面积是49平方厘米.
【点评】解答此题的关键是弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.
【分析】组合图形的面积等于底为6厘米,高为4厘米的三角形面积加长为6厘米,宽为4厘米的长方形的面积,根据三角形和长方形的面积公式解答即可.
【解答】解:
(平方厘米)
答:组合图形的面积是36平方厘米.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
【分析】观察图形,根据梯形的定义可得,阴影部分是一个梯形,而阴影部分梯形的面积与空白处的上底是8厘米、下底是20厘米、高是10厘米的梯形的面积相等,据此利用梯形的面积公式计算出空白处的梯形的面积即可解答问题.
【解答】解:根据题干分析可得,①阴影部分是一个特殊的四边形,它是 梯形.
②求阴影部分的面积是:
(平方厘米)
答:阴影部分的面积是140平方厘米.
故答案为:梯.
【点评】此题主要考查了梯形的定义以及梯形的面积公式的计算应用.
【分析】由题意可知,等底等高的三角形的面积是平行四边形的面积的一半,所以两个三角形的总面积是长方形的面积的一半,据此即可得解.
【解答】解:(平方米);
答:两个三角形的总面积是20平方米.
故答案为:20.
【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/3/25 19:33:52;用户:田老师;邮箱:zlpx8888@xyh.com;学号:36103138
一.组合图形的面积(共40小题)
1.下图中的两个正方形的边长分别为8厘米和5厘米,求阴影部分的面积.
2.北京某四合院子正好是个边长10米的正方形,在院子中央修了一条宽2米的“十字形”的路,如图.这条“十字形”路的面积是多少平方米?
3.求梯形中阴影部分的面积.(单位:厘米)
4.如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.长方形的面积是多少?
5.如图所示,直角梯形的面积为225平方厘米,厘米,厘米,三角形的面积为100平方厘米.阴影部分的面积是多少平方厘米?
6.如图的三角形分成两部分,甲的面积是,乙的面积是 .
7.如图,已知四边形中,,,厘米,厘米,求四边形的面积.
8.图中,是边长为8厘米的正方形.
(1)三角形的面积是多少?
(2)三角形的面积比三角形的面积大6平方厘米,求阴影部分的面积.
9.求下面组合图形的面积.
10.计算组合图形的面积.
11.计算下列组合图形的面积
12.(如图)平行四边形的底是3.6米,髙是2.5米.求阴影部分的面积.
13.计算下面组合图形的面积.(单位
14.计算下面阴影部分的面积.
15.求图形中阴影部分的面积(单位:厘米
16.计算下面组合图形的面积.
17.计算图形的面积
18.求如图阴影部分的面积.(单位:分米)
19.已知如图空白部分的面积是求阴影部分的面积.
20.一块草坪的形式如图所示,请你用两种方法算出它的面积.
第一种方法: ;
第二种方法: .
21.求如图阴影部分的面积.
22.一张边长为12厘米的正方形纸,从一边的中点到邻边的中点连一条线段.沿这条线段剪去一个角(如图),剩下的面积是多少?
23.求如图阴影部分的面积.
(1) ;
(2)平行四边形的面积是
24.多边形相关内容计算
①平行四边形的面积是6.3平方厘米,高7厘米,求它的底长.
②一块三角形的玻璃,它的底是,高是.它的面积是多少?
③求阴影部分面积.
25.计算图中阴影部分的面积.
26.如图,两个正方形的边长分别为6厘米和4厘米,求阴影部分的面积是多少?
27.计算下列图形阴影部分的面积(单位:分米)
28.如图:在梯形中,厘米,厘米,的面积是10平方厘米米,求阴影部分的面积.
29.图中阴影部分的面积是 平方厘米.
30.一个长方形(如图),阴影部分面积是45平方米,这个大长方形的面积是
平方米.
31.如图中,四边形的面积是 .
32.如图,平行四边形的面积是72平方米,那么图中阴影部分的面积是 平方米.
33.如图,长方形中,,,是的中点,,为上任意一点,则阴影部分的总面积是 .
34.在正方形中,切去四个三角形得到一个五边形(如图,其中所标的数表示各线段的长度),线段将五边形分成两个面积相等的部分,那么的长度是 .
35.两个相同的长方形,长为20厘米,宽为9厘米,按如图叠放在一起.这个图形的面积是多少平方厘米?
36.如图(单位:厘米)是两个相同的直角梯形重叠在一起.求阴影部分的面积.
37.如图,把一张长19厘米,宽13厘米的长方形白纸折成右图形壮,厘米,求阴影部分的面积.
38.求如图组合图形的面积.(单位:厘米)
39.一个长方形与一个平行四边形交叠在一起,如图所示.(单位:厘米)
①阴影部分是一个特殊的四边形,它是 形.
②求阴影部分的面积.
40.如图:长方形面积是40平方米,点是一边上的中点,那么两个三角形的总面积是 平方米.
沪教版五年级上册《组合图形的面积》2019年同步练习卷
参考答案与试题解析
一.组合图形的面积(共40小题)
【分析】根据题意,阴影部分的面积等于梯形的面积减去三角形的面积,根据梯形的面积公式和三角形的面积公式进行计算即可得到答案.
【解答】解:如图
梯形的面积为:
,
,
(平方厘米),
三角形的面积为:
,
(平方厘米),
阴影部分的面积为:(平方厘米),
答:阴影部分的面积为52.5平方厘米.
【点评】解答此题的关键是将阴影部分与三角形看作是一个梯形,然后再用梯形的面积减去三角形的面积即可.
【分析】此题可以利用平移,把除路以外的地方利用平移拼成一个新的正方形,其边长即为原正方形的边长减去路宽,然后用原正方形的面积减去新正方形的面积即可得到路的面积.
【解答】解:
(平方米);
答:这条“十字形”路的面积是36平方米.
【点评】本题实质上是利用了转化的思想方法,结合平移,把不规则图形的面积转化为规则图形的面积的和或差来解决.
【分析】根据图意可知,阴影部分的面积等于梯形的面积减去空白三角形的面积,据此代入数据计算即可解答.
【解答】解:
(平方厘米)
答:阴影部分的面积是135平方厘米.
【点评】本题主要考查组合图形的面积,熟练找出阴影部分是由哪几部分的和或差得到的是解答本题的关键.
【分析】如图所示,由题意可知:三角形①、②、③、④应均为等腰直角三角形,且①和③组成1个边长为4厘米的正方形,②和④能组成1个边长为12厘米的正方形,用大正方形的面积分别减去这两个小正方形的面积,就是长方形的面积.
【解答】解:由题意可得:(厘米),
(厘米),
所以长方形的面积是:
,
,
(平方厘米);
答:长方形的面积是96平方厘米.
【点评】解答此题的关键是:利用其他图形的面积和或差求出长方形的面积.
【分析】直角梯形的面积和上、下底已知,则可以利用梯形的面积公式求出的长度,又因三角形的面积和底边已知,则可以求出边上的高的长度,进而可以求出三角形的边上的高,于是即可求出三角形的面积,用梯形的面积分别减去两个空白三角形的面积,就是阴影部分的面积.
【解答】解:如图所示:
的长度:
(厘米);
的长度:
(厘米);
的长度:
(厘米)
三角形的面积:
(平方厘米);
阴影部分的面积:
(平方厘米)
答:阴影部分的面积是100平方厘米.
【点评】此题主要考查梯形和三角形的面积公式的灵活应用.
【分析】观察图得出甲三角形的底是乙三角形底的2倍,两个三角形的高相等,所以乙三角形的面积是甲三角形的面积的一半.
【解答】解:因为甲三角形的底是乙三角形底的2倍,两个三角形的高相等,
所以乙三角形的面积是:(平方厘米),
答:乙的面积是5平方厘米;
故答案为:5.
【点评】关键是根据题意得出高相等的两个三角形,它们的面积比就是底的比.
【分析】如图,
观察图示可知,四边形的面积底和高为12厘米的大等腰直角三角形面积底和高为4厘米的小等腰直角三角形面积,根据三角形面积公式,代入数据,进一步解答即可.
【解答】解:
(平方厘米)
答:四边形的面积是64平方厘米.
【点评】组合图形的面积计算,可以根据几何图形的特征,通过分割、割补、平移、翻折、对称、旋转等方法,化复杂为简单,变组合图形为基本图形的加减组合.
【分析】(1)三角形的底为8厘米,高为8厘米,运用三角形面积公式:,解决问题.
(2)根据题意,三角形比三角形面积大6平方厘米,那么三角形的面积比正方形的面积大6平方厘米,可利用正方形的面积加上6平方厘米就是三角形的的面积,设为厘米,得,解方程求出的长,再利用三角形面积公式求出阴影部分的面积即可.
【解答】解:(1)
(平方厘米)
答:三角形的面积是32平方厘米.
(2)设为厘米,得:
(平方厘米)
答:阴影部分的面积是38平方厘米.
【点评】此题考查了三角形面积公式的灵活运用.第二问:关键在于求得的长度.
【分析】如图所示:将每个图形分割成一个长方形和一个三角形,然后利用长方形和三角形的面积公式即可求解.
【解答】解:
(平方厘米)
答:这个图形的面积是84平方厘米.
(平方厘米)
答:这个图形的面积是48平方厘米.
【点评】解答此题的关键是将图形分割成规则图形,再根据规则图形的面积公式进行解答即可.
【分析】这个图形的面积三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:
答:这个图形的面积是525.
【点评】此题主要考查三角形和平行四边形的面积公式的灵活应用.
【分析】这两个图形的面积都等于三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:(1)
答:这个图形的面积是24.
(2)
答:这个图形的面积是20.125.
【点评】此题主要考查三角形和平行四边形的面积公式的灵活应用.
【分析】观察图形知道,阴影部分的面积就是底是3.6米,髙是2.5米的三角形的面积,利用三角形的面积公式即可解答.
【解答】解:
(平方米)
答:阴影部分的面积是4.5平方米.
【点评】不同的阴影部分的面积就是平行四边形的面积的一半.
【分析】(1)组合图形的面积平行四边形的面积三角形的面积,利用三角形和平行四边形的面积公式即可求解;
(2)组合图形的面积两个正方形面积之和下面梯形的面积,运用正方形和梯形面积公式解答即可.
【解答】解:(1)
(平方厘米)
答:组合图形的面积是218平方厘米.
(2)
(平方厘米)
答:组合图形的面积是9.5平方厘米.
【点评】解答此题的关键是:将图形分割成规则图形,再利用规则图形的面积和或差求解.
【分析】(1)阴影部分的面积梯形的面积空白部分的面积,于是利用梯形的面积公式和三角形的面积公式即可求解.
(2)阴影部分的面积三角形的面积平行四边形的面积,利用三角形的面积公式和平行四边形的面积公式即可求解.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是63.2平方厘米.
(2)
(平方厘米)
答:阴影部分的面积是59.52平方厘米.
【点评】此题主要考查梯形、三角形和平行四边形的面积公式的灵活应用.
【分析】阴影部分的面积梯形形的面积长方形的面积,然后根据梯形的面积公式和长方形的面积公式解答即可.
【解答】解:
(平方厘米)
答:阴影部分的面积是105平方厘米.
【点评】本题考查了圆与组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
【分析】根据题意,组合图形的面积平行四边形的面积梯形的面积,运用平行四边形的面积公式:,梯形的面积公式:,计算即可.
【解答】解:
(平方厘米)
答:组合图形的面积为62.5平方厘米.
【点评】此题也可把此组合图形看作梯形,上底为厘米,下底为厘米,运用梯形面积公式列式为:.
【分析】由图意可知:这个图形由一个三角形和一个平行四边形组成,利用三角形和平行四边形的面积公式即可求解.因为三角形是一个等腰直角三角形,因此平行四边形的底为3.5,然后运用三角形和平行四边形的面积公式解答即可.
【解答】解:
答:图形的面积是20.125.
【点评】此题主要考查利用规则图形的面积和求图形的面积,关键求出平行四边形的底的长度.
【分析】阴影部分的面积等于长方形的面积减去空白三角形的面积,利用长方形的面积公式,和三角形的面积公式即可求解.
【解答】解:
(平方分米)
答:阴影部分的面积是560平方分米.
【点评】此题主要考查长方形和三角形的面积公式的灵活应用.
【分析】由三角形的面积公式可得:,据此即可求出空白部分的高,也就等于知道了阴影部分的高,再利用三角形的面积公式即可求解.
【解答】解:
(厘米)
(平方厘米)
答:阴影部分的面积是15平方厘米.
【点评】此题主要考查三角形的面积公式的灵活应用.
【分析】(1)如图所示:这个图形的面积梯形的面积长方形的面积,据此利用长方形和梯形的面积公式即可求解.
(2)这个图形的面积长方形的面积三角形的面积,据此利用三角方形和梯形的面积公式即可求解.
【解答】解:(1)
(平方米)
答:这块草坪的面积是90平方米.
(2)
(平方米)
答:这块草坪的面积是90平方米.
故答案为:,.
【点评】解答此题的关键是:将图形分割成两个规则图形再解答即可.
【分析】(1)影部分的面积长方形的面积空白三角形的面积.据此解答.
(2)阴影部分的面积大方形面积小正方形面积空白三角形面积.据此解答.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是42平方厘米.
(2)
(平方厘米)
答:阴影部分的面积是92平方厘米.
【点评】在求不规则图形的面积时,一般要把不规则图形的面积转化为几个规则图形的面积相加或相减的方法进行计算.
【分析】剩余部分的面积正方形的面积三角形的面积,正方形的边长是12分米,三角形的两条边是分米,根据正方形和三角形的面积进行计算即可.据此解答.
【解答】解:
(平方分米)
答:剩下的面积是126平方分米.
【点评】本题主要考查了学生对正方形和三角形面积公式的掌握.
【分析】(1)平行四边形和空白部分(三角形)等底等高,所以平行四边形的面积就等于三角形的面积的2倍,也就是说阴影部分和空白部分的面积相等,于是利用三角形的面积公式即可求解;
(2)先用平行四边形的面积48平方分米,除以它的底8分米,即可得出平行四边形的高,也就等于知道了阴影部分的高,于是利用三角形的面积公式即可求解.
【解答】解:(1)
(平方厘米)
答:阴影部分的面积是104平方厘米.
(2)
(平方分米)
答:阴影部分的面积是12平方分米.
故答案为:104平方厘米.
【点评】此题主要考查平行四边形和三角形的面积公式的灵活应用.
【分析】(1)根据平行四边形的面积公式可得:平行四边形的底面积高,据此计算即可解答问题.
(2)根据三角形的面积公式底高计算出玻璃的面积即可.
(3)阴影部分的面积等于大长方形的面积减去空白部分梯形的面积,据此代入数据计算即可解答.
【解答】解:①(厘米)
答:它的底长是0.9厘米.
②
(平方厘米)
答:它的面积是48.75平方厘米.
③
(平方米)
答:阴影部分面积是17平方米.
【点评】本题主要考查平行四边形、三角形长方形、梯形的面积公式,熟练掌握公式是解答本题的关键.
【分析】阴影部分可看做两个三角形,直接运用三角形面积公式计算出每个三角形的面积,再相加即可.
【解答】解:
答:阴影部分的面积为51.5.
【点评】此题主要考查学生对三角形面积公式的掌握情况.
【分析】要求阴影部分的面积,我们先求出2个正方形的面积,用2个正方形的面积的和减去大正方形面积的一半,再减去大三角形的面积就是阴影部分的面积.
【解答】解:
(平方厘米)
答:图中阴影部分的面积14平方厘米.
【点评】本题运用正方形的面积公式及三角形的面积公式进行计算,考查了学生灵活解决问题的能力.
【分析】(1)用两个正方形的面积和减去直角三角形的面积即可.
(2)用长方形的面积减去梯形的面积即可解答.
【解答】解:(1),
,
(平方分米);
(2),
,
(平方分米).
【点评】本题主要考查了组合图形的面积,解题关键是熟练掌握长方形、正方形、梯形、三角形的面积公式.
【分析】如图所示,空白三角形的面积已知,利用三角形的面积公式即可求出这个三角形的高,也就等于知道了梯形的高,进而利用梯形的面积公式即可求解.
【解答】解:(厘米),
,
,
,
(平方厘米);
(平方厘米);
答:阴影部分的面积是22.5平方厘米.
【点评】此题主要考查三角形和梯形的面积的计算方法,关键是先求出三角形的高.
【分析】由于平行四边形里的两个三角形是等高的,它们的底加起来是平行四边形的长30,高是平行四边形的高12,所以两个三角形面积之和等于平行四方形面积的一半,根据平行四边形的面积公式,进行解答即可.
【解答】解:
(平方厘米)
答:阴影部分的面积是180平方厘米.
故答案为:180.
【点评】此题考查了三角形面积和平行四边形面积的求法,只要找出它们之间的数量关系进行解答即可.
【分析】依据三角形的面积是与其等底等高的长方形面积的一半,即可进行解答.
【解答】解:(平方米);
答:这个大长方形的面积是90平方米.
故答案为:90.
【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形(长方形)面积的一半.
【分析】如图,延长、,交点为,则得出一个大等腰直角三角形,并画出斜边上的高线,则厘米,所以大等腰直角三角形的面积等于平方厘米,则这个四边形的面积等于大等腰直角三角形的面积,减去上面的直角边长为4厘米的小等腰直角三角形的面积,据此计算即可解答问题.
【解答】解:根据题干分析可得:延长、,交点为,则得出一个大等腰直角三角形,并画出斜边上的高线,则厘米,
(平方厘米)
答:四边形的面积是41平方厘米.
故答案为:41.
【点评】解答此题的关键是画出合适的辅助线,利用等腰直角三角形的性质和三角形的面积公式计算即可解答问题.
【分析】空白三角形与平行四边形等底等高,所以三角形的面积是平行四边形的面积的一半,那么阴影部分的面积是平行四边形的面积的一半,用平行四边形的面积除以2即可求出阴影部分的面积.
【解答】解:(平方米)
答:图中阴影部分的面积是 36平方米.
故答案为:36.
【点评】解决本题关键是明确:三角形的面积是和它等底等高的平行四边形面积的一半.
【分析】我们做一条辅助线即连接,与的高的长度是,因为,所以这两个三角形的面积的和较容易解答了,的面积比较容易解得.
【解答】解:连接,
厘米,
阴影部分的面积是:
,
,
,
,
,
,
(平方厘米);
故答案为:324.
【点评】本题是一道复杂的组合图形,考查了学生对三角形的面积公式的运用情况.
【分析】由题意可知:正方形的面积减去4个三角形的面积,就能得到中间五边形的面积,进而求出四边形的面积,于是即可求得梯形的面积,从而利用梯形的面积公式即可求出的长度,进而得出的长度.
【解答】解:四边形的面积为:
,
,
,
,
;
设的长度为,
则,
,
,
,
;
答:的长度是3.25.
故答案为:3.25.
【点评】解答此题的关键是先求出中间五边形的面积,进而得到梯形的面积,问题即可得解.
【分析】这个图形面积比原来减少了重叠部分的边长为9厘米的正方形的面积,然后根据长方形的面积长宽,求出一个长方形的面积,再乘2,求出两个长方形的面积,然根据正方形的面积边长边长求出正方形的面积,再作差.
【解答】解:
(平方厘米)
答:这个图形的面积是279平方厘米.
【点评】解决本题注意观察图,找清楚这个图形的组成部分,再利用长方形和正方形的面积公式求解.
【分析】由题意可知:阴影部分的面积就等于空白的较大一点的梯形的面积,这个梯形的下底和高已知,上底可以求出,从而可以求其面积,也就求得了阴影部分的面积.
【解答】解:,
,
,
,
(平方厘米);
答:阴影部分的面积是140平方厘米.
【点评】解答此题的关键是明白:阴影部分的面积就等于空白的较大一点的梯形的面积.
【分析】如图所示,阴影部分的面积梯形的面积折过来的部分的面积,又因梯形的上底、下底和高分别为5.5厘米、13厘米和19厘米,折过来的部分的两条直角边分别为厘米、19厘米,从而利用梯形和三角形的面积公式即可求解.
【解答】解:
(平方厘米)
答:阴影部分的面积是49平方厘米.
【点评】解答此题的关键是弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.
【分析】组合图形的面积等于底为6厘米,高为4厘米的三角形面积加长为6厘米,宽为4厘米的长方形的面积,根据三角形和长方形的面积公式解答即可.
【解答】解:
(平方厘米)
答:组合图形的面积是36平方厘米.
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.
【分析】观察图形,根据梯形的定义可得,阴影部分是一个梯形,而阴影部分梯形的面积与空白处的上底是8厘米、下底是20厘米、高是10厘米的梯形的面积相等,据此利用梯形的面积公式计算出空白处的梯形的面积即可解答问题.
【解答】解:根据题干分析可得,①阴影部分是一个特殊的四边形,它是 梯形.
②求阴影部分的面积是:
(平方厘米)
答:阴影部分的面积是140平方厘米.
故答案为:梯.
【点评】此题主要考查了梯形的定义以及梯形的面积公式的计算应用.
【分析】由题意可知,等底等高的三角形的面积是平行四边形的面积的一半,所以两个三角形的总面积是长方形的面积的一半,据此即可得解.
【解答】解:(平方米);
答:两个三角形的总面积是20平方米.
故答案为:20.
【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/3/25 19:33:52;用户:田老师;邮箱:zlpx8888@xyh.com;学号:36103138
同课章节目录
