三年级上 册数学试题 面积课课练(含答案)沪教版
文档属性
| 名称 | 三年级上 册数学试题 面积课课练(含答案)沪教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-27 00:00:00 | ||
图片预览




文档简介
沪教版三年级上学期《4.3 面积》2020年同步练习卷
一.面积及面积的大小比较(共40小题)
1.如图,阴影部分面积相等答案完成正确的是
A.①② B.①②④ C.①②③ D.①②③④
2.如图是两个形状大小完全一样的长方形.比较两幅图的阴影面积,说法正确的是
A.甲乙 B.甲乙 C.甲乙
3.如图两个平行四边形的面积相等.其中图1的平行四边形由两个同样大小的梯形拼成,阴影部分的梯形与三角形面积比较的结果是
A.梯形面积大 B.三角形面积大 C.面积一样大
4.周长相等的长方形、正方形和圆形,关于它们的面积,下列哪种说法正确
A.长方形的面积最大 B.正方形的面积最大
C.圆形的面积最大 D.无法确定
5.下列选项中 所示的阴影所占的比例和如图长方形中阴影所占的比例最接近.
A. B. C. D.
6.如图是在平行线间的五个图形,它们的面积相比较
A. B. C. D.
E.
7.如图三幅图是在同样大的正方形中分别画出的图形,三幅图中的阴影面积相比较,结果是
A.①面积最小 B.②面积最大 C.③面积最大 D.同样大
8.如图是三个边长都是12厘米的正方形,阴影部分
A.周长相等 B.面积相等
C.面积和周长都相等 D.面积和周长都不相等
9.一个长方体,它的长、宽、高分别是10厘米、8厘米、12厘米,在它的6个面中最大的面的面积是 平方厘米.
A.80 B.96 C.120 D.150
10.比较下面两个图形,说法正确的是
A.甲、乙的面积相等,周长也相等
B.甲、乙的面积相等,但甲的周长长
C.甲、乙的周长相等,但乙的面积大
D.甲的面积小,周长也小
11.比较如图两个图形,说法正确的是
A.甲和乙的面积相等,周长也相等
B.甲和乙的面积相等,但甲的周长长
C.甲和乙的周长相等,但乙的面积大
D.甲的面积小,周长也小
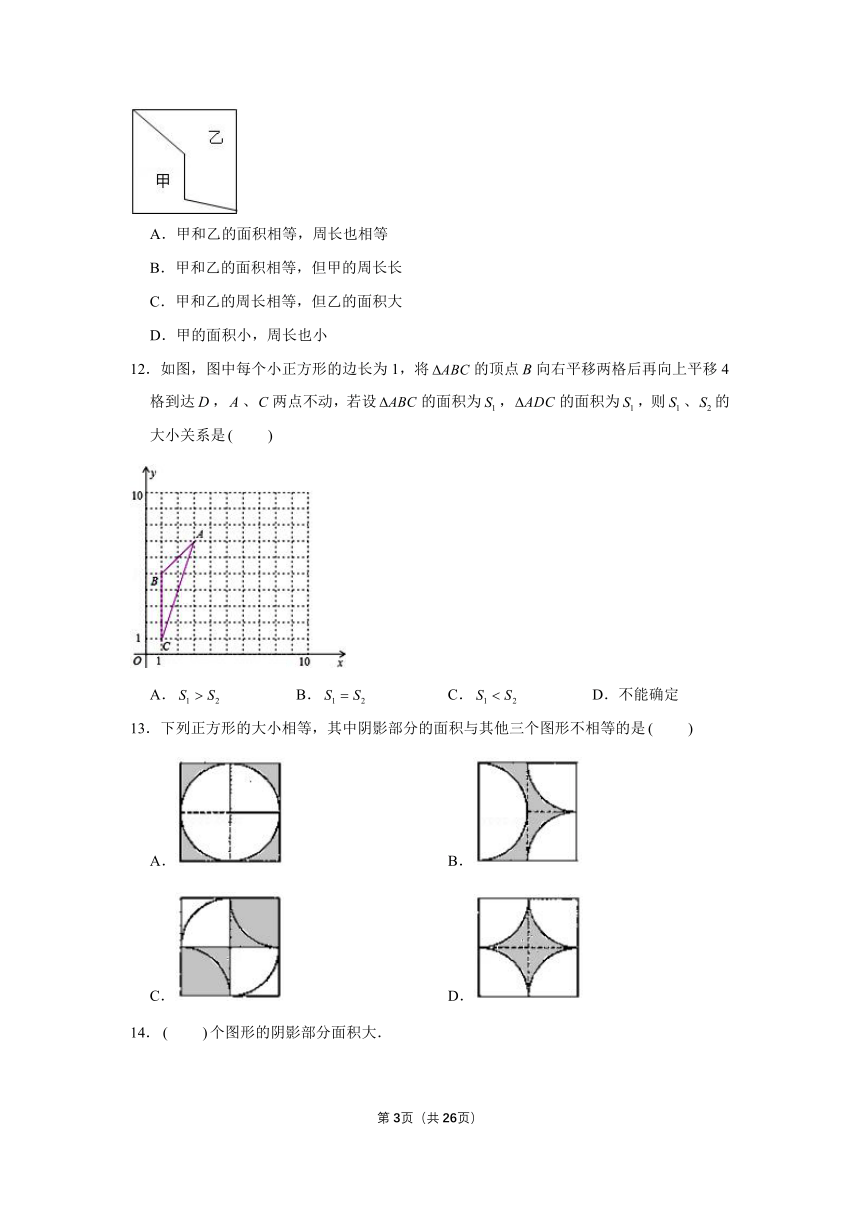
12.如图,图中每个小正方形的边长为1,将的顶点向右平移两格后再向上平移4格到达,、两点不动,若设的面积为,的面积为,则、的大小关系是
A. B. C. D.不能确定
13.下列正方形的大小相等,其中阴影部分的面积与其他三个图形不相等的是
A. B.
C. D.
14. 个图形的阴影部分面积大.
A.图形大 B.图形大 C.一样大
15.用四根木条钉成的长方形,拉成平行四边形后,面积变小了. .
16.甲与乙的周长相比 ,甲与乙的面积相比 .
.甲乙;
.甲乙;
.甲乙.
17. 号图形与的面积一样大.
....
18.如图:阴影甲的面积和阴影乙的面积相差 平方分米.
19.把三张大小相同的正方形卡片、、叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图1摆放时,阴影部分的面积为;若按图2摆放时,阴影部分的面积为,则 (填“”、“ ”或“” .
20.如图所示,圆的直径与相互垂直,以为圆心,为半径画弧.其中和的面积关系是 .,,
21.在图中,长方形地分成两部分,比较甲乙两块地的周长和面积.
甲面积 乙面积;甲周长 乙周长.
22.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等. (判断对错)
23.如果两个正方形的周长相等,那么它的面积也相等. .(判断对错)
24.如图,每个方格表示1平方厘米.
号图的面积最大, 号图的面积最小.
25.如图中,每个方格表示1平方厘米
号图的面积最大, 号图的面积最小.
26.动物王国里,小猴给动物们分地,大家对分配结果都很满意,只有狐狸和狼争论不休.狐狸家分到平行四边形这块地,狼家分到平行四边形这块地,最后小猴的解释让他们满意而归,你知道小猴是怎么解释的吗?
27.如图所示,每个小圆的直径是10厘米,那么黑色部分的面积大还是阴影部分的面积大?
28.仔细观察,在边长20厘米的正方形中,哪几个图阴影部分的面积是相等的?
29.先把图形编号,再数一数,将下列图形的面积从大到小排列.
30.数学小博士.
(1)比一比,谁的面积大,用“”标出.
(2)你能算出阴影部分的面积吗?
31.如图两个边长为的正方形,在其中一个正方形里面画一个最大的圆,在另一个正方形里面画四个一样大的圆,比较两个正方形中圆的面积大小.
32.如图,在两块完全相同的正方形钢板上冲制小圆片,甲钢板上冲制了4个,乙钢板上冲制了9个.剩下的边角料哪一块多?为什么?
33.一个养禽户用一段长16米的篱笆靠一面墙围成一个长方形养鸡场,求占地面积最大时是多少平方米?长与宽取整数.
34.图中每小格的面积是,把图补完整,使格子图中的图形面积为.
35.下面方格中那个图形的面积最大?请打“”
若每格是,图1面积是 ,图2面积是 .
36.如图中与图①面积相等的图形有哪些? .
37.下面图形的面积有什么关系?你是怎样想的?
38.观察与比较
(1)左图中各图形的面积有什么关系,请你写出3条.
(2)你知道哪些比较图形的方法(至少写出三种)
39.向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4中不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植的月季花的面积最大?
40.哪种图形面积最大?
有一根绳子长31.4米,小明、小强和小红想用它在植物园围出一块草地.要使得围出的这块地的面积尽可能大,小明说应该围成长方形,小红认为应该围成正方形.小强认为应该围成圆形,三人争执不下.“实践是检验真理的唯一标准”,他们三人受这句话的启发,决定先一个一个算出面积来.
①如果用这根绳子围成长方形(长和宽不相等),那么这个长方形的面积是多少?例如取长10米(用计算器帮助计算)
②如果用这根绳子围成一个正方形,那么这个正方形的面积是多少?
③如果用这根绳子围成一个圆形,那么这个圆形的面积是多少?
④上面三种形状的图形,哪一种面积最大?
沪教版三年级上学期《4.3 面积》2020年同步练习卷
参考答案与试题解析
一.面积及面积的大小比较(共40小题)
【分析】在平行四边形①②中和长方形③中,阴影部分面积都是平行四边形或者长方形面积的一半,梯形的上底加下底也是4厘米,也等于平行四边形面积的一半,由此即可判断它们面积的大小.
【解答】解:前三图中,阴影部分均为平行四边形(长方形)面积的一半,而三个平行四边形(长方形)的面积相等;
梯形的上底加下底也是4厘米,也等于平行四边形面积的一半;
由此可得:阴影部分的面积都相等.
故选:.
【点评】此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.
【分析】我们分别求出甲乙两个图形的面积,然后进行比较即可.我们设出这两个长方形的长都是宽都是,表示出阴影部分的面积,再进行选择.
【解答】解:甲图阴影部分的面积:
,
;
乙图阴影部分的面积:
,
;
甲图的面积乙图的面积,
即一样大.
故选:.
【点评】本题考查了三角形面积公式的运用,考查了学生灵活运用公式解决问题.
【分析】根据三角形的面积等于和它等底等高的平行四边形面积的一半,又知图1和图2是两个面积相等的平行四边形,那么两幅图的阴影部分的面积相等.
【解答】解:图1和图2是两个面积相等的平行四边形,
图1中,
图2中,
因此阴影部分的梯形与阴影三角形面积一样大;
故选:.
【点评】此题主要根据等底等高的三角形的面积等于平行四边形面积的一半,来解决这个问题.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁的面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的面积为:;
正方形的边长为:,面积为:;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的长方形、正方形和圆形,圆形的面积最大,长方形的面积最小.
故选:.
【点评】此题主要考查长方形、正方形、圆形的面积公式及灵活运用.
【分析】把图中的一个小正方形看作1,则共有18个小正方形,阴影部分为8,由此得出长方形中阴影部分占,由此得出答案.
【解答】解:把图中的一个小正方形看作1,
长方形中阴影部分占,
故选:.
【点评】本题主要考查了求一个数的另一个数的百分之几,用除法列式解答.
【分析】由图意可知:这几个图形的高都相等,可以假设出高,再分别利用梯形、平行四边形、三角形的面积公式求出其面积,即可进行判断.
【解答】解:假设高为6,
则梯形的面积
,
;
2个平行四边形等底等高,所以面积相等,即为;
2个三角形等底等高,所以面积相等,即为;
所以这五个图形的面都相等.
故选:.
【点评】解答此题的关键是:假设出高,分别求其面积,再比较大小即可.
【分析】三幅图,正方形的面积一样大.
图(1)中,阴影的面积等于正方形的面积减去4个圆心角为的扇形的面积,而4个圆心角为的扇形的面积,就是一个圆的面积.
(2)阴影的面积等于正方形的面积减去2个半圆的面积.2个半圆的面积就是一个圆的面积.
(3)阴影的面积等于正方形的面积减去1个圆的面积.
所以三幅图的阴影部分的面积都是正方形的面积减去圆的面积.
【解答】解:由分析可得:
三幅图的阴影部分的面积都是正方形的面积减去圆的面积,所以这三幅图的阴影部分的面积同样大.
故选:.
【点评】本题考查不规则图形面积的计算及大小比较.
【分析】由题意可知:剪法1:剩下的铁皮的面积正方形的面积一个大圆的面积,剪法2:剩下的铁皮的面积正方形的面积个大圆的面积;剪法3:剩下的铁皮的面积正方形的面积个小圆的面积;正方形的边长是12厘米,则能求出正方形的面积和圆的面积,从而求得剩下的铁皮的面积.
【解答】解:剪法1和剪法2:因为正方形的边长是12厘米,
则正方形的面积是:(平方厘米);
剪法1:圆的半径是(厘米);
剩下的铁皮的面积是,
,
(平方厘米);
剪法:3:圆的半径是(厘米);
剩下的铁皮的面积是,
,
(平方厘米);
答:剩下的铁皮面积一样大.
故选:.
【点评】解答此题的关键是明白:剩下的铁皮的面积正方形的面积圆的面积,只要补充上直径的长度,即可求解.
【分析】根据题意可知,它的6个面中最大的面的面积是这个长方体的最大面的面积,即平方厘米.
【解答】解:(平方厘米)
答:在它的6个面中最大的面的面积是120平方厘米.
故选:.
【点评】此题考查的目的是理解掌握长方体的特征,以及长方形的面积的计算方法.
【分析】根据面积和周长的意义知:面积是图形所占平面的大小,周长是围成平面图形线段的长度和.据此解答.
【解答】解:根据周长的意义,甲、乙两图形的周长都是一个长一个宽曲线的长.所以它们的周长相等.
根据面积的意义,图形乙的面积明显大于图形甲的面积.
故它们的面积是乙大于甲.
故选:.
【点评】本题主要考查了学生根据面积和周长意义解答问题的能力.
【分析】由图形可知,甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以乙的面积大于甲的面积;因为甲的周长长方形的两条邻边的和中间的曲线的长,乙的周长长方形的两条邻边和中间的曲线的长,进行解答继而得出结论.
【解答】解:如图:
因为甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,
所以甲的面积小于乙的面积;
甲的周长长方形的两条邻边的和中间的曲线的长,
乙的周长长方形的两条邻边的和中间的曲线的长,
所以甲的周长等于乙的周长;
故选:.
【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.
【分析】先找出点,然后连接、,以为底,高为2,以为底,高为2,即三角形和三角形的高相等,三角形的底是4,三角形的底是2,根据三角形的面积计算公式可以分别求出两个三角形的面积,然后比较即可.
【解答】解:如图:
三角形的面积,
三角形的面积,
因为,
所以;
故选:.
【点评】此题考查了面积及面积大小比较,明确三角形的面积计算公式,是解答此题的关键.
【分析】选项、、中的阴影部分的面积都等于正方形的面积减去空白部分圆的面积,这三个图形中阴影部分的面积是相等,而选项中的阴影部分的面积等于正方形的面积减去空白部分两个小正方形的面积,所以选项的阴影部分的面积与其他三个图形不相等.
【解答】解:、、中的阴影部分的面积都等于正方形的面积减去空白部分圆的面积,而选项中的阴影部分的面积等于正方形的面积减去空白部分两个小正方形的面积,所以选项的阴影部分的面积与其他三个图形不相等.
故选:.
【点评】此题考查了面积及等积变换,将阴影面积转化为易求的图形的面积的差或和是解题的常用方法.
【分析】分别数出两个图形中阴影小方格的数量,然后把小方格的数量进行比较,即可.
【解答】解:的面积是8个小方格的面积,的面积是8个小方格的面积,
所以和的面积相等;
故选:.
【点评】数出两个图形中阴影小方格的数量,是解答此题的关键.
【分析】由题意可知:用四根木条钉成的长方形,拉成平行四边形后,四条边的长度不变,但是高变短了,也就是原来长方形的宽变短了,则依据长方形和平行四边形的面积公式可知,图形的面积变小了,据此解答即可.
【解答】解:用四根木条钉成的长方形,拉成平行四边形后,四条边的长度不变,但是高变短了,
也就是原来长方形的宽变短了,
则依据长方形和平行四边形的面积公式可知,图形的面积变小了,
故答案为:.
【点评】解答此题的关键是明白:每条边的长度及高的变化情况,进而依据面积公式,即可判断.
【分析】则甲的周长长方形的长宽中间折线的长,乙的周长长方形的长宽中间折线的长,可知甲乙周长一样;连接,因为图中虚线两旁的面积各占长方形面积的一半,则显然甲的面积大于乙的面积.
【解答】解;如图作辅助线
甲的周长长方形的长宽中间折线的长,乙的周长长方形的长宽中间折线的长,可知甲乙周长一样;
因为虚线两旁的长方形面积相等,
则可知甲的面积乙的面积.
故选:、.
【点评】本题考查了面积与面积的大小比较以及周长与周长的大小比较,解题时要善于灵活应用长方形的性质.
【分析】本题采用割补的方法,将图上面的凸出部分补到图形的右边凹进部分,即可形成与长、宽相等的长方形.于是和的面积一样大;将的右边凸出部分补到左边凹进部分,也得到和一样的长方形.所以和的面积也一样大;可以看作的四角各去掉一个小长方形后得到的图形,因此的面积比要小.
【解答】解:由以上分析可知,如下图所示:
、的面积和的面积一样大,的面积比小.
故选:.
【点评】根据图形特点,适当的进行割补是解答此题的关键.
【分析】因为空白三角形的面积既属于小正方形的面积,又属于大正方形的面积,所以求阴影甲的面积和阴影乙的面积的差,也就是求大正方形和小正方形的面积差,根据:正方形的面积边长边长,分别求出大正方形和小正方形的面积,然后用大正方形的面积小正方形的面积即可.
【解答】解:
(平方分米)
答:阴影甲的面积和阴影乙的面积相差9平方分米.
故答案为:9.
【点评】明确阴影甲的面积和阴影乙的面积的差,也就是求大正方形和小正方形的面积差,是解答此题的关键;用到的知识点:正方形面积计算公式的应用.
【分析】根据正方形的性质,可以把两块阴影部分合并后计算面积,然后,比较和的大小.
【解答】解:设底面的正方形的边长为,正方形卡片,,的边长为,
由图1,得
,
由图2,得
,
所以
故答案为:.
【点评】本题主要考查了列代数式的知识,解题的关键是根据正方形四条边相等的性质得出和的面积,难度不大.
【分析】设圆的半径为,则的面积等于两个直角边长为的等腰直角三角形面积之和,即.但这个面积又等于,故;弯月形的面积等于,再减去以直角为中心角的扇形的面积,即;故弯月形面积与面积相等;据此解答.
【解答】解:根据以上分析知:
设圆的半径是,
.
又,
所以.
弯月形面积半圆的面积.
所以的面积等于弯月形的面积;
故答案为:.
【点评】本题的关键是根据图形之间的关系,进行分析解答问题的能力.
【分析】如下图,根据周长是指围成一个图形的所有边长的总和,由此知道乙的周长是曲线的长度,甲图形的周长是曲线的长度,再根据长方形的特征,知道,,由此得出甲、乙两个图形的周长相等.乙的面积大于长方形面积的一半,甲的面积小于长方形面积的一半,由此得出:一定面积大于甲的面积.
【解答】解:因为,乙图形的周长是:曲线的长度,
甲图形的周长是:曲线的长度,
而,,
所以,甲、乙两个图形的周长相等;
乙的面积大于长方形面积的一半,甲的面积小于长方形面积的一半.
所以乙的面积比甲大;
故答案为:小于,等于.
【点评】此题主要考查了周长的定义、面积的定义及长方形的特征.
【分析】因为太极图是旋转对称图形,即一条白鱼和黑鱼的面积相等,然后同时加上一个小圆的面积(眼睛),可得:图中阴阳(即圈内黑白)两部分的面积相等;由此即可判断.
【解答】解:由分析可知:图中阴阳(即圈内黑白)两部分的面积相等;
故答案为:.
【点评】本题考查了旋转对称图形:如果某一个图形围绕某一点旋转一定的角度(小于后能与原图形重合,那么这个图形就叫做旋转对称图形.常见的旋转对称图形有:线段,正多边形,平行四边形,圆等.
【分析】根据“两个正方形的周长相等”,用周长除以4得边长,可知它们的边长一定相等;边长一定相等了,那么面积用边长乘边长,也一定相等.
【解答】解:两个正方形的周长相等,面积也相等.
故答案为:.
【点评】此题考查正方形周长与面积的计算方法.
【分析】因为每个小方格表示1平方厘米,分别数出3个图形所占的小方格的个数,进而得出三个图形的面积,然后比较即可.
【解答】解:由图可知:①中小方格共有9个,面积是9平方厘米,
②中小方格共有10个,面积是10平方厘米,
③中大方格共有3个,相当于6个小方格面积,面积是6平方厘米,
因为,
所以②号图的面积最大,③号图的面积最小.
故答案为:②,③.
【点评】此题考查了面积及面积大小比较,数出每个图形中小方格的个数,是解答此题的关键.
【分析】图一为梯形,用长5厘米、宽为3厘米的长方形的面积底为3厘米、高为3厘米的三角形底为3厘米、高为3厘米的三角形底为1厘米、高为1厘米的三角形;
图二先根据梯形的面积计算公式:梯形的面积(上底下底)高,求出梯形的面积,用梯形的面积,减去一个小正方形的面积即可;
图三用长5厘米、宽为3厘米的长方形的面积个小正方形的面积即可;
然后比较三个图形的面积即可.
【解答】解:①的面积
(平方厘米);
②的面积:
(平方厘米);
③的面积:(平方厘米);
因为8平方厘米平方厘米平方厘米,
所以(3)号图的面积最大,(1)号图的面积最小.
故答案为:(3),(1).
【点评】此题主要考查梯形的面积(上底下底)高、长方形的面积长宽,三角形的面积底高.
【分析】因为三角形和平行四边形等底等高,所以三角形的面积是平行四边形面积的一半;因为三角形又和平行四边形等底等高,所以三角形的面积是平行四边形面积的一半;由此即可得出结论.
【解答】解:因为三角形和平行四边形等底等高,所以三角形的面积平行四边形面积;
因为三角形和平行四边形等底等高,所以三角形的面积平行四边形面积;
所以平行四边形和平行四边形面积面积相等.
【点评】明确三角形的面积等于和它等高的平行四边形面积的一半,是解答此题的关键.
【分析】设小圆的交叉部分的面积和为,在小圆外、大圆内阴影部分的面积和为,解答本题只需表示出,即可得出和的大小关系.
【解答】解:大圆的半径为10,则小圆半径是,
即.
答:黑色部分的面积等于阴影部分的面积.
【点评】本题考查面积及等积变换,比较简单,关键是在表示的大小注意计算了两次,别忘了减去后才是的大小
【分析】由题意可知:四个图中阴影部分的面积正方形的面积圆的面积,由此即可判断.
【解答】解:四个图中阴影部分的面积正方形的面积圆的面积,因为边长相等,圆的直径相等,所以四个图形中阴影部分的面积相等.
【点评】明确每个图中阴影部分的面积正方形的面积圆的面积,是解答此题的关键.
【分析】根据数方格可知:①的面积是9,②的面积是3,③的面积是4,④的面积是5,⑤的面积是6;然后根据数的大小比较的方法,按照从大到小的顺序进行排列即可.
【解答】解:①的面积是9,②的面积是3,③的面积是4,④的面积是5,⑤的面积是6;
因为,
所以①⑤④③②.
【点评】此题考查里面积及面积大小比较,明确每个图形的面积,是解答此题的关键.
【分析】(1)假设每个小正方形的边长为1厘米,分别计算出每个图形的面积,即可比较大小;左图的面积为长6厘米、宽2厘米的长方形的面积加上底8厘米、高3厘米的三角形的面积再加上上底1厘米、下底2厘米、高1厘米的梯形的面积;右图的面积为底为2厘米、高1厘米的三角形的面积加上底4厘米、高2厘米的三角形的面积再加上长4厘米、宽2厘米的长方形的面积.利用长方形、三角形和梯形的面积公式,代入数据求出即可.
(2)观察图形可知,阴影部分的面积等于长为100米、宽为60米的长方形的面积减去长为米、宽为米的长方形的面积.
【解答】解:(1)假设每个小正方形的边长为1厘米,
则左图的面积为:
(平方厘米),
右图的面积:
(平方厘米),
因为,
所以左图的面积大;
(2)
(平方米),
答:阴影部分的面积是3200平方米.
故答案为:(1)
(2)3200平方米.
【点评】(1)分别计算出每个图形的面积,是解答本题的关键.(2)关键是善于利用规则图形的面积的和差来求出不规则图形的面积.
【分析】在其中一个正方形里面画一个最大的圆,圆的直径等于正方形的边长,根据圆的面积公式可求面积;在另一个正方形里面画四个一样大的圆,圆的直径等于正方形的边长除以2,根据圆的面积公式可求1个的面积,再乘以4可求4个的面积;再比较大小即可求解.
【解答】解:
故两个正方形中圆的面积大小相等.
【点评】考查了圆的面积计算,本题关键是得到两个图形中圆的直径的长度.
【分析】根据题干,只要比较出剩下的边角料的面积大小即可解决问题.剩下边角料的面积正方形的面积冲制的圆的面积之和.
【解答】解:设两个正方形的边长为,则甲中圆的半径为:,乙中的圆的半径为,
甲剩下的部分为:
;
乙剩下的部分为:
,
,
,
所以甲乙剩下部分的面积相等,即剩下的边角料一样多.
答:剩下的边角料一样多.
【点评】此题考查了在正方体中切割等圆的方法,得出每个圆的半径是解决此类问题的关键.设边长是是为了半径是整数,方便计算.
【分析】设养鸡场宽为米,则长为米,利用列表法列举出组成长方形的长与宽,由面积公式分别计算出它们的面积即可解决问题.
【解答】解:设养鸡场宽为米,则长为米,根据题意,将可以组成的长方形的长与宽列举出来,并计算出它们的面积如下:
由表可知,占地面积最大时是32平方米.
答:占地面积最大时是32平方米.
【点评】本题主要考查长方形面积的大小比较,借助列表法来解决实际问题比较简单,关键是根据题意设出宽,并表示出长,再根据实际讨论这个长方形的长与宽的各种不同情况并计算出相应的面积再进行比较即可.
【分析】根据题意,图中每小格的面积是1平方厘米,只要在图中画出一个包含13个小格的图形即可.
【解答】解:
【点评】此题考查的目的是掌握利用数方格的方法求平面图形的面积的方法,不满格的按半格计算.
【分析】每个小正方形的边长已知,则计算几个图形的面积所需要的线段的长度就可求,从而可以求出它们的面积.
【解答】解:如图所示:
第一个图形的面积:;
图1面积是:;
图2面积是:;
第四个图形的面积:.
故答案为:8,9.
【点评】此题主要考查长方形、正方形、梯形和三角形面积的计算方法,关键是先求出计算面积所需要的线段的长度.
【分析】先分别求出各图形的面积,然后进行比较即可得出结论.
【解答】解:图①:;
图②:;
图③:;
图④:;
图⑤:进行平移、拼接,得到的图⑤的面积是:;
图⑥:;
和图①面积相等的是图③④;
故答案为:③④.
【点评】此题考查的知识点:三角形、长方形、正方形、梯形的面积计算公式.
【分析】设相邻两个点之间的距离为1,则可以判断出每个图形的长宽(或底高),分别根据各自的面积公式求出面积即可判断.
【解答】解:设相邻两个点之间的距离为1,那么
(1)第一个图形是长宽分别为4和5的长方形,其面积为:;
(2)第二个图形是底和高分别为4和5的平行四边形,其面积为:;
(3)第三个图形是底和高分别为4和5的三角形,其面积为:;
(4)第四个图形是上底为1下底为3高为5的梯形,其面积为:;
所以各图形面积之间的关系是:前两个图形面积相等,后两个图形面积相等,且前两个图形的面积等于后两个图形的面积的2倍.
【点评】本题考查了面积及面积的大小比较,表示出各个图形的面积是解决问题的关键.
【分析】图形的面积有3种关系,即大于,等于,小于;比较图形的方法有:①计算法.②拼合法.③方格计算法.
【解答】解:(1)左图中各图形的面积有三种情况:
第一组:①③的和等于④,
第二组:①②的和等于④,
第三组:①②的和等于③,
(2)比较图形的方法有:
①计算法.
②拼合法.
③方格计算法.
【点评】面积有3种关系大于,等于,小于.比较图形的方法有:①计算法.②拼合法.③方格计算法.
【分析】设正方形边长为,将第1个图形中的半圆的面积相加为以半径为的圆,种植月季花的面积即正方形的面积减去半径为的圆的面积;第2个图形种植月季花的面积即正方形的面积减去半径为的圆的面积,第3个图形中4个扇形的面积相加为以半径为的圆,即种植月季花的面积即正方形的面积减去半径为的圆的面积;故第1,2,3个图形阴影的面积都为正方形的面积减去以为半径的圆的面积;第4个图形的面积为正方形的面积减去空白面积,即两个半径为的圆的面积和减去边长为的正方形的面积,由此计算后比较即可.
【解答】解:第1,2,3个图形的面积为:;
第4个图形的面积为:
;
因为,
所以方案④种植月季花的面积最大.
【点评】本题主要考查了面积及面积大小比较,解决本题的关键是将每个图形阴影部分面积求出,然后进行比较.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是10米,
则圆的面积为:(米;
正方形的边长为:,面积为:(平方米);
长方形长宽越接近面积越大,就取长为3宽为2,面积为:(平方米),
当长方形的长和宽最接近时面积也小于6.25平方米;
所以周长相等的正方形、长方形和圆形,圆面积最大.
答:如果用这根绳子围成长方形(长和宽不相等),那么这个长方形的面积是6平方米;
如果用这根绳子围成一个正方形,那么这个正方形的面积是6.25平方米;
如果用这根绳子围成一个圆形,那么这个圆形的面积是7.96平方米;
上面三种形状的图形,圆的面积最大.
【点评】此题主要考查长方形、正方形、圆形的面积公式及灵活运用,解答此题可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/3/25 19:27:55;用户:田老师;邮箱:zlpx8888@xyh.com;学号:36103138
第1页(共1页)
一.面积及面积的大小比较(共40小题)
1.如图,阴影部分面积相等答案完成正确的是
A.①② B.①②④ C.①②③ D.①②③④
2.如图是两个形状大小完全一样的长方形.比较两幅图的阴影面积,说法正确的是
A.甲乙 B.甲乙 C.甲乙
3.如图两个平行四边形的面积相等.其中图1的平行四边形由两个同样大小的梯形拼成,阴影部分的梯形与三角形面积比较的结果是
A.梯形面积大 B.三角形面积大 C.面积一样大
4.周长相等的长方形、正方形和圆形,关于它们的面积,下列哪种说法正确
A.长方形的面积最大 B.正方形的面积最大
C.圆形的面积最大 D.无法确定
5.下列选项中 所示的阴影所占的比例和如图长方形中阴影所占的比例最接近.
A. B. C. D.
6.如图是在平行线间的五个图形,它们的面积相比较
A. B. C. D.
E.
7.如图三幅图是在同样大的正方形中分别画出的图形,三幅图中的阴影面积相比较,结果是
A.①面积最小 B.②面积最大 C.③面积最大 D.同样大
8.如图是三个边长都是12厘米的正方形,阴影部分
A.周长相等 B.面积相等
C.面积和周长都相等 D.面积和周长都不相等
9.一个长方体,它的长、宽、高分别是10厘米、8厘米、12厘米,在它的6个面中最大的面的面积是 平方厘米.
A.80 B.96 C.120 D.150
10.比较下面两个图形,说法正确的是
A.甲、乙的面积相等,周长也相等
B.甲、乙的面积相等,但甲的周长长
C.甲、乙的周长相等,但乙的面积大
D.甲的面积小,周长也小
11.比较如图两个图形,说法正确的是
A.甲和乙的面积相等,周长也相等
B.甲和乙的面积相等,但甲的周长长
C.甲和乙的周长相等,但乙的面积大
D.甲的面积小,周长也小
12.如图,图中每个小正方形的边长为1,将的顶点向右平移两格后再向上平移4格到达,、两点不动,若设的面积为,的面积为,则、的大小关系是
A. B. C. D.不能确定
13.下列正方形的大小相等,其中阴影部分的面积与其他三个图形不相等的是
A. B.
C. D.
14. 个图形的阴影部分面积大.
A.图形大 B.图形大 C.一样大
15.用四根木条钉成的长方形,拉成平行四边形后,面积变小了. .
16.甲与乙的周长相比 ,甲与乙的面积相比 .
.甲乙;
.甲乙;
.甲乙.
17. 号图形与的面积一样大.
....
18.如图:阴影甲的面积和阴影乙的面积相差 平方分米.
19.把三张大小相同的正方形卡片、、叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图1摆放时,阴影部分的面积为;若按图2摆放时,阴影部分的面积为,则 (填“”、“ ”或“” .
20.如图所示,圆的直径与相互垂直,以为圆心,为半径画弧.其中和的面积关系是 .,,
21.在图中,长方形地分成两部分,比较甲乙两块地的周长和面积.
甲面积 乙面积;甲周长 乙周长.
22.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等. (判断对错)
23.如果两个正方形的周长相等,那么它的面积也相等. .(判断对错)
24.如图,每个方格表示1平方厘米.
号图的面积最大, 号图的面积最小.
25.如图中,每个方格表示1平方厘米
号图的面积最大, 号图的面积最小.
26.动物王国里,小猴给动物们分地,大家对分配结果都很满意,只有狐狸和狼争论不休.狐狸家分到平行四边形这块地,狼家分到平行四边形这块地,最后小猴的解释让他们满意而归,你知道小猴是怎么解释的吗?
27.如图所示,每个小圆的直径是10厘米,那么黑色部分的面积大还是阴影部分的面积大?
28.仔细观察,在边长20厘米的正方形中,哪几个图阴影部分的面积是相等的?
29.先把图形编号,再数一数,将下列图形的面积从大到小排列.
30.数学小博士.
(1)比一比,谁的面积大,用“”标出.
(2)你能算出阴影部分的面积吗?
31.如图两个边长为的正方形,在其中一个正方形里面画一个最大的圆,在另一个正方形里面画四个一样大的圆,比较两个正方形中圆的面积大小.
32.如图,在两块完全相同的正方形钢板上冲制小圆片,甲钢板上冲制了4个,乙钢板上冲制了9个.剩下的边角料哪一块多?为什么?
33.一个养禽户用一段长16米的篱笆靠一面墙围成一个长方形养鸡场,求占地面积最大时是多少平方米?长与宽取整数.
34.图中每小格的面积是,把图补完整,使格子图中的图形面积为.
35.下面方格中那个图形的面积最大?请打“”
若每格是,图1面积是 ,图2面积是 .
36.如图中与图①面积相等的图形有哪些? .
37.下面图形的面积有什么关系?你是怎样想的?
38.观察与比较
(1)左图中各图形的面积有什么关系,请你写出3条.
(2)你知道哪些比较图形的方法(至少写出三种)
39.向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4中不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植的月季花的面积最大?
40.哪种图形面积最大?
有一根绳子长31.4米,小明、小强和小红想用它在植物园围出一块草地.要使得围出的这块地的面积尽可能大,小明说应该围成长方形,小红认为应该围成正方形.小强认为应该围成圆形,三人争执不下.“实践是检验真理的唯一标准”,他们三人受这句话的启发,决定先一个一个算出面积来.
①如果用这根绳子围成长方形(长和宽不相等),那么这个长方形的面积是多少?例如取长10米(用计算器帮助计算)
②如果用这根绳子围成一个正方形,那么这个正方形的面积是多少?
③如果用这根绳子围成一个圆形,那么这个圆形的面积是多少?
④上面三种形状的图形,哪一种面积最大?
沪教版三年级上学期《4.3 面积》2020年同步练习卷
参考答案与试题解析
一.面积及面积的大小比较(共40小题)
【分析】在平行四边形①②中和长方形③中,阴影部分面积都是平行四边形或者长方形面积的一半,梯形的上底加下底也是4厘米,也等于平行四边形面积的一半,由此即可判断它们面积的大小.
【解答】解:前三图中,阴影部分均为平行四边形(长方形)面积的一半,而三个平行四边形(长方形)的面积相等;
梯形的上底加下底也是4厘米,也等于平行四边形面积的一半;
由此可得:阴影部分的面积都相等.
故选:.
【点评】此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.
【分析】我们分别求出甲乙两个图形的面积,然后进行比较即可.我们设出这两个长方形的长都是宽都是,表示出阴影部分的面积,再进行选择.
【解答】解:甲图阴影部分的面积:
,
;
乙图阴影部分的面积:
,
;
甲图的面积乙图的面积,
即一样大.
故选:.
【点评】本题考查了三角形面积公式的运用,考查了学生灵活运用公式解决问题.
【分析】根据三角形的面积等于和它等底等高的平行四边形面积的一半,又知图1和图2是两个面积相等的平行四边形,那么两幅图的阴影部分的面积相等.
【解答】解:图1和图2是两个面积相等的平行四边形,
图1中,
图2中,
因此阴影部分的梯形与阴影三角形面积一样大;
故选:.
【点评】此题主要根据等底等高的三角形的面积等于平行四边形面积的一半,来解决这个问题.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁的面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的面积为:;
正方形的边长为:,面积为:;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的长方形、正方形和圆形,圆形的面积最大,长方形的面积最小.
故选:.
【点评】此题主要考查长方形、正方形、圆形的面积公式及灵活运用.
【分析】把图中的一个小正方形看作1,则共有18个小正方形,阴影部分为8,由此得出长方形中阴影部分占,由此得出答案.
【解答】解:把图中的一个小正方形看作1,
长方形中阴影部分占,
故选:.
【点评】本题主要考查了求一个数的另一个数的百分之几,用除法列式解答.
【分析】由图意可知:这几个图形的高都相等,可以假设出高,再分别利用梯形、平行四边形、三角形的面积公式求出其面积,即可进行判断.
【解答】解:假设高为6,
则梯形的面积
,
;
2个平行四边形等底等高,所以面积相等,即为;
2个三角形等底等高,所以面积相等,即为;
所以这五个图形的面都相等.
故选:.
【点评】解答此题的关键是:假设出高,分别求其面积,再比较大小即可.
【分析】三幅图,正方形的面积一样大.
图(1)中,阴影的面积等于正方形的面积减去4个圆心角为的扇形的面积,而4个圆心角为的扇形的面积,就是一个圆的面积.
(2)阴影的面积等于正方形的面积减去2个半圆的面积.2个半圆的面积就是一个圆的面积.
(3)阴影的面积等于正方形的面积减去1个圆的面积.
所以三幅图的阴影部分的面积都是正方形的面积减去圆的面积.
【解答】解:由分析可得:
三幅图的阴影部分的面积都是正方形的面积减去圆的面积,所以这三幅图的阴影部分的面积同样大.
故选:.
【点评】本题考查不规则图形面积的计算及大小比较.
【分析】由题意可知:剪法1:剩下的铁皮的面积正方形的面积一个大圆的面积,剪法2:剩下的铁皮的面积正方形的面积个大圆的面积;剪法3:剩下的铁皮的面积正方形的面积个小圆的面积;正方形的边长是12厘米,则能求出正方形的面积和圆的面积,从而求得剩下的铁皮的面积.
【解答】解:剪法1和剪法2:因为正方形的边长是12厘米,
则正方形的面积是:(平方厘米);
剪法1:圆的半径是(厘米);
剩下的铁皮的面积是,
,
(平方厘米);
剪法:3:圆的半径是(厘米);
剩下的铁皮的面积是,
,
(平方厘米);
答:剩下的铁皮面积一样大.
故选:.
【点评】解答此题的关键是明白:剩下的铁皮的面积正方形的面积圆的面积,只要补充上直径的长度,即可求解.
【分析】根据题意可知,它的6个面中最大的面的面积是这个长方体的最大面的面积,即平方厘米.
【解答】解:(平方厘米)
答:在它的6个面中最大的面的面积是120平方厘米.
故选:.
【点评】此题考查的目的是理解掌握长方体的特征,以及长方形的面积的计算方法.
【分析】根据面积和周长的意义知:面积是图形所占平面的大小,周长是围成平面图形线段的长度和.据此解答.
【解答】解:根据周长的意义,甲、乙两图形的周长都是一个长一个宽曲线的长.所以它们的周长相等.
根据面积的意义,图形乙的面积明显大于图形甲的面积.
故它们的面积是乙大于甲.
故选:.
【点评】本题主要考查了学生根据面积和周长意义解答问题的能力.
【分析】由图形可知,甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以乙的面积大于甲的面积;因为甲的周长长方形的两条邻边的和中间的曲线的长,乙的周长长方形的两条邻边和中间的曲线的长,进行解答继而得出结论.
【解答】解:如图:
因为甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,
所以甲的面积小于乙的面积;
甲的周长长方形的两条邻边的和中间的曲线的长,
乙的周长长方形的两条邻边的和中间的曲线的长,
所以甲的周长等于乙的周长;
故选:.
【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.
【分析】先找出点,然后连接、,以为底,高为2,以为底,高为2,即三角形和三角形的高相等,三角形的底是4,三角形的底是2,根据三角形的面积计算公式可以分别求出两个三角形的面积,然后比较即可.
【解答】解:如图:
三角形的面积,
三角形的面积,
因为,
所以;
故选:.
【点评】此题考查了面积及面积大小比较,明确三角形的面积计算公式,是解答此题的关键.
【分析】选项、、中的阴影部分的面积都等于正方形的面积减去空白部分圆的面积,这三个图形中阴影部分的面积是相等,而选项中的阴影部分的面积等于正方形的面积减去空白部分两个小正方形的面积,所以选项的阴影部分的面积与其他三个图形不相等.
【解答】解:、、中的阴影部分的面积都等于正方形的面积减去空白部分圆的面积,而选项中的阴影部分的面积等于正方形的面积减去空白部分两个小正方形的面积,所以选项的阴影部分的面积与其他三个图形不相等.
故选:.
【点评】此题考查了面积及等积变换,将阴影面积转化为易求的图形的面积的差或和是解题的常用方法.
【分析】分别数出两个图形中阴影小方格的数量,然后把小方格的数量进行比较,即可.
【解答】解:的面积是8个小方格的面积,的面积是8个小方格的面积,
所以和的面积相等;
故选:.
【点评】数出两个图形中阴影小方格的数量,是解答此题的关键.
【分析】由题意可知:用四根木条钉成的长方形,拉成平行四边形后,四条边的长度不变,但是高变短了,也就是原来长方形的宽变短了,则依据长方形和平行四边形的面积公式可知,图形的面积变小了,据此解答即可.
【解答】解:用四根木条钉成的长方形,拉成平行四边形后,四条边的长度不变,但是高变短了,
也就是原来长方形的宽变短了,
则依据长方形和平行四边形的面积公式可知,图形的面积变小了,
故答案为:.
【点评】解答此题的关键是明白:每条边的长度及高的变化情况,进而依据面积公式,即可判断.
【分析】则甲的周长长方形的长宽中间折线的长,乙的周长长方形的长宽中间折线的长,可知甲乙周长一样;连接,因为图中虚线两旁的面积各占长方形面积的一半,则显然甲的面积大于乙的面积.
【解答】解;如图作辅助线
甲的周长长方形的长宽中间折线的长,乙的周长长方形的长宽中间折线的长,可知甲乙周长一样;
因为虚线两旁的长方形面积相等,
则可知甲的面积乙的面积.
故选:、.
【点评】本题考查了面积与面积的大小比较以及周长与周长的大小比较,解题时要善于灵活应用长方形的性质.
【分析】本题采用割补的方法,将图上面的凸出部分补到图形的右边凹进部分,即可形成与长、宽相等的长方形.于是和的面积一样大;将的右边凸出部分补到左边凹进部分,也得到和一样的长方形.所以和的面积也一样大;可以看作的四角各去掉一个小长方形后得到的图形,因此的面积比要小.
【解答】解:由以上分析可知,如下图所示:
、的面积和的面积一样大,的面积比小.
故选:.
【点评】根据图形特点,适当的进行割补是解答此题的关键.
【分析】因为空白三角形的面积既属于小正方形的面积,又属于大正方形的面积,所以求阴影甲的面积和阴影乙的面积的差,也就是求大正方形和小正方形的面积差,根据:正方形的面积边长边长,分别求出大正方形和小正方形的面积,然后用大正方形的面积小正方形的面积即可.
【解答】解:
(平方分米)
答:阴影甲的面积和阴影乙的面积相差9平方分米.
故答案为:9.
【点评】明确阴影甲的面积和阴影乙的面积的差,也就是求大正方形和小正方形的面积差,是解答此题的关键;用到的知识点:正方形面积计算公式的应用.
【分析】根据正方形的性质,可以把两块阴影部分合并后计算面积,然后,比较和的大小.
【解答】解:设底面的正方形的边长为,正方形卡片,,的边长为,
由图1,得
,
由图2,得
,
所以
故答案为:.
【点评】本题主要考查了列代数式的知识,解题的关键是根据正方形四条边相等的性质得出和的面积,难度不大.
【分析】设圆的半径为,则的面积等于两个直角边长为的等腰直角三角形面积之和,即.但这个面积又等于,故;弯月形的面积等于,再减去以直角为中心角的扇形的面积,即;故弯月形面积与面积相等;据此解答.
【解答】解:根据以上分析知:
设圆的半径是,
.
又,
所以.
弯月形面积半圆的面积.
所以的面积等于弯月形的面积;
故答案为:.
【点评】本题的关键是根据图形之间的关系,进行分析解答问题的能力.
【分析】如下图,根据周长是指围成一个图形的所有边长的总和,由此知道乙的周长是曲线的长度,甲图形的周长是曲线的长度,再根据长方形的特征,知道,,由此得出甲、乙两个图形的周长相等.乙的面积大于长方形面积的一半,甲的面积小于长方形面积的一半,由此得出:一定面积大于甲的面积.
【解答】解:因为,乙图形的周长是:曲线的长度,
甲图形的周长是:曲线的长度,
而,,
所以,甲、乙两个图形的周长相等;
乙的面积大于长方形面积的一半,甲的面积小于长方形面积的一半.
所以乙的面积比甲大;
故答案为:小于,等于.
【点评】此题主要考查了周长的定义、面积的定义及长方形的特征.
【分析】因为太极图是旋转对称图形,即一条白鱼和黑鱼的面积相等,然后同时加上一个小圆的面积(眼睛),可得:图中阴阳(即圈内黑白)两部分的面积相等;由此即可判断.
【解答】解:由分析可知:图中阴阳(即圈内黑白)两部分的面积相等;
故答案为:.
【点评】本题考查了旋转对称图形:如果某一个图形围绕某一点旋转一定的角度(小于后能与原图形重合,那么这个图形就叫做旋转对称图形.常见的旋转对称图形有:线段,正多边形,平行四边形,圆等.
【分析】根据“两个正方形的周长相等”,用周长除以4得边长,可知它们的边长一定相等;边长一定相等了,那么面积用边长乘边长,也一定相等.
【解答】解:两个正方形的周长相等,面积也相等.
故答案为:.
【点评】此题考查正方形周长与面积的计算方法.
【分析】因为每个小方格表示1平方厘米,分别数出3个图形所占的小方格的个数,进而得出三个图形的面积,然后比较即可.
【解答】解:由图可知:①中小方格共有9个,面积是9平方厘米,
②中小方格共有10个,面积是10平方厘米,
③中大方格共有3个,相当于6个小方格面积,面积是6平方厘米,
因为,
所以②号图的面积最大,③号图的面积最小.
故答案为:②,③.
【点评】此题考查了面积及面积大小比较,数出每个图形中小方格的个数,是解答此题的关键.
【分析】图一为梯形,用长5厘米、宽为3厘米的长方形的面积底为3厘米、高为3厘米的三角形底为3厘米、高为3厘米的三角形底为1厘米、高为1厘米的三角形;
图二先根据梯形的面积计算公式:梯形的面积(上底下底)高,求出梯形的面积,用梯形的面积,减去一个小正方形的面积即可;
图三用长5厘米、宽为3厘米的长方形的面积个小正方形的面积即可;
然后比较三个图形的面积即可.
【解答】解:①的面积
(平方厘米);
②的面积:
(平方厘米);
③的面积:(平方厘米);
因为8平方厘米平方厘米平方厘米,
所以(3)号图的面积最大,(1)号图的面积最小.
故答案为:(3),(1).
【点评】此题主要考查梯形的面积(上底下底)高、长方形的面积长宽,三角形的面积底高.
【分析】因为三角形和平行四边形等底等高,所以三角形的面积是平行四边形面积的一半;因为三角形又和平行四边形等底等高,所以三角形的面积是平行四边形面积的一半;由此即可得出结论.
【解答】解:因为三角形和平行四边形等底等高,所以三角形的面积平行四边形面积;
因为三角形和平行四边形等底等高,所以三角形的面积平行四边形面积;
所以平行四边形和平行四边形面积面积相等.
【点评】明确三角形的面积等于和它等高的平行四边形面积的一半,是解答此题的关键.
【分析】设小圆的交叉部分的面积和为,在小圆外、大圆内阴影部分的面积和为,解答本题只需表示出,即可得出和的大小关系.
【解答】解:大圆的半径为10,则小圆半径是,
即.
答:黑色部分的面积等于阴影部分的面积.
【点评】本题考查面积及等积变换,比较简单,关键是在表示的大小注意计算了两次,别忘了减去后才是的大小
【分析】由题意可知:四个图中阴影部分的面积正方形的面积圆的面积,由此即可判断.
【解答】解:四个图中阴影部分的面积正方形的面积圆的面积,因为边长相等,圆的直径相等,所以四个图形中阴影部分的面积相等.
【点评】明确每个图中阴影部分的面积正方形的面积圆的面积,是解答此题的关键.
【分析】根据数方格可知:①的面积是9,②的面积是3,③的面积是4,④的面积是5,⑤的面积是6;然后根据数的大小比较的方法,按照从大到小的顺序进行排列即可.
【解答】解:①的面积是9,②的面积是3,③的面积是4,④的面积是5,⑤的面积是6;
因为,
所以①⑤④③②.
【点评】此题考查里面积及面积大小比较,明确每个图形的面积,是解答此题的关键.
【分析】(1)假设每个小正方形的边长为1厘米,分别计算出每个图形的面积,即可比较大小;左图的面积为长6厘米、宽2厘米的长方形的面积加上底8厘米、高3厘米的三角形的面积再加上上底1厘米、下底2厘米、高1厘米的梯形的面积;右图的面积为底为2厘米、高1厘米的三角形的面积加上底4厘米、高2厘米的三角形的面积再加上长4厘米、宽2厘米的长方形的面积.利用长方形、三角形和梯形的面积公式,代入数据求出即可.
(2)观察图形可知,阴影部分的面积等于长为100米、宽为60米的长方形的面积减去长为米、宽为米的长方形的面积.
【解答】解:(1)假设每个小正方形的边长为1厘米,
则左图的面积为:
(平方厘米),
右图的面积:
(平方厘米),
因为,
所以左图的面积大;
(2)
(平方米),
答:阴影部分的面积是3200平方米.
故答案为:(1)
(2)3200平方米.
【点评】(1)分别计算出每个图形的面积,是解答本题的关键.(2)关键是善于利用规则图形的面积的和差来求出不规则图形的面积.
【分析】在其中一个正方形里面画一个最大的圆,圆的直径等于正方形的边长,根据圆的面积公式可求面积;在另一个正方形里面画四个一样大的圆,圆的直径等于正方形的边长除以2,根据圆的面积公式可求1个的面积,再乘以4可求4个的面积;再比较大小即可求解.
【解答】解:
故两个正方形中圆的面积大小相等.
【点评】考查了圆的面积计算,本题关键是得到两个图形中圆的直径的长度.
【分析】根据题干,只要比较出剩下的边角料的面积大小即可解决问题.剩下边角料的面积正方形的面积冲制的圆的面积之和.
【解答】解:设两个正方形的边长为,则甲中圆的半径为:,乙中的圆的半径为,
甲剩下的部分为:
;
乙剩下的部分为:
,
,
,
所以甲乙剩下部分的面积相等,即剩下的边角料一样多.
答:剩下的边角料一样多.
【点评】此题考查了在正方体中切割等圆的方法,得出每个圆的半径是解决此类问题的关键.设边长是是为了半径是整数,方便计算.
【分析】设养鸡场宽为米,则长为米,利用列表法列举出组成长方形的长与宽,由面积公式分别计算出它们的面积即可解决问题.
【解答】解:设养鸡场宽为米,则长为米,根据题意,将可以组成的长方形的长与宽列举出来,并计算出它们的面积如下:
由表可知,占地面积最大时是32平方米.
答:占地面积最大时是32平方米.
【点评】本题主要考查长方形面积的大小比较,借助列表法来解决实际问题比较简单,关键是根据题意设出宽,并表示出长,再根据实际讨论这个长方形的长与宽的各种不同情况并计算出相应的面积再进行比较即可.
【分析】根据题意,图中每小格的面积是1平方厘米,只要在图中画出一个包含13个小格的图形即可.
【解答】解:
【点评】此题考查的目的是掌握利用数方格的方法求平面图形的面积的方法,不满格的按半格计算.
【分析】每个小正方形的边长已知,则计算几个图形的面积所需要的线段的长度就可求,从而可以求出它们的面积.
【解答】解:如图所示:
第一个图形的面积:;
图1面积是:;
图2面积是:;
第四个图形的面积:.
故答案为:8,9.
【点评】此题主要考查长方形、正方形、梯形和三角形面积的计算方法,关键是先求出计算面积所需要的线段的长度.
【分析】先分别求出各图形的面积,然后进行比较即可得出结论.
【解答】解:图①:;
图②:;
图③:;
图④:;
图⑤:进行平移、拼接,得到的图⑤的面积是:;
图⑥:;
和图①面积相等的是图③④;
故答案为:③④.
【点评】此题考查的知识点:三角形、长方形、正方形、梯形的面积计算公式.
【分析】设相邻两个点之间的距离为1,则可以判断出每个图形的长宽(或底高),分别根据各自的面积公式求出面积即可判断.
【解答】解:设相邻两个点之间的距离为1,那么
(1)第一个图形是长宽分别为4和5的长方形,其面积为:;
(2)第二个图形是底和高分别为4和5的平行四边形,其面积为:;
(3)第三个图形是底和高分别为4和5的三角形,其面积为:;
(4)第四个图形是上底为1下底为3高为5的梯形,其面积为:;
所以各图形面积之间的关系是:前两个图形面积相等,后两个图形面积相等,且前两个图形的面积等于后两个图形的面积的2倍.
【点评】本题考查了面积及面积的大小比较,表示出各个图形的面积是解决问题的关键.
【分析】图形的面积有3种关系,即大于,等于,小于;比较图形的方法有:①计算法.②拼合法.③方格计算法.
【解答】解:(1)左图中各图形的面积有三种情况:
第一组:①③的和等于④,
第二组:①②的和等于④,
第三组:①②的和等于③,
(2)比较图形的方法有:
①计算法.
②拼合法.
③方格计算法.
【点评】面积有3种关系大于,等于,小于.比较图形的方法有:①计算法.②拼合法.③方格计算法.
【分析】设正方形边长为,将第1个图形中的半圆的面积相加为以半径为的圆,种植月季花的面积即正方形的面积减去半径为的圆的面积;第2个图形种植月季花的面积即正方形的面积减去半径为的圆的面积,第3个图形中4个扇形的面积相加为以半径为的圆,即种植月季花的面积即正方形的面积减去半径为的圆的面积;故第1,2,3个图形阴影的面积都为正方形的面积减去以为半径的圆的面积;第4个图形的面积为正方形的面积减去空白面积,即两个半径为的圆的面积和减去边长为的正方形的面积,由此计算后比较即可.
【解答】解:第1,2,3个图形的面积为:;
第4个图形的面积为:
;
因为,
所以方案④种植月季花的面积最大.
【点评】本题主要考查了面积及面积大小比较,解决本题的关键是将每个图形阴影部分面积求出,然后进行比较.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是10米,
则圆的面积为:(米;
正方形的边长为:,面积为:(平方米);
长方形长宽越接近面积越大,就取长为3宽为2,面积为:(平方米),
当长方形的长和宽最接近时面积也小于6.25平方米;
所以周长相等的正方形、长方形和圆形,圆面积最大.
答:如果用这根绳子围成长方形(长和宽不相等),那么这个长方形的面积是6平方米;
如果用这根绳子围成一个正方形,那么这个正方形的面积是6.25平方米;
如果用这根绳子围成一个圆形,那么这个圆形的面积是7.96平方米;
上面三种形状的图形,圆的面积最大.
【点评】此题主要考查长方形、正方形、圆形的面积公式及灵活运用,解答此题可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/3/25 19:27:55;用户:田老师;邮箱:zlpx8888@xyh.com;学号:36103138
第1页(共1页)
同课章节目录
- 一、复习与提高
- 小复习
- 连乘、连除
- 正方形组成的图形——多连块
- 二、用一位数乘
- 乘整十数、整百数
- 看图列式
- 一位数与两位数相乘
- 一位数与三位数相乘
- 小练习(1)
- 三、时间的初步认识(三)
- 年、月、日
- 平年和闰年
- 制作年历
- 小练习(2)
- 四、用一位数除
- 整十数、整百数的除法
- 两位数被一位数除
- 三位数被一位数除
- 除法的应用
- 单价、数量、总价
- 小练习(3)
- 五、几何小实践
- 千米的认识
- 米与厘米
- 分米的认识
- 轴对称图形
- 三角形的分类(2)
- 面积
- 正方形与长方形的面积
- 平方米
- 六、整理与提高
- 乘乘除除
- 解决问题
- 图形的拼嵌
- 它们有多大
- 计算小胖家的面积
- 数学广场——植树问题
- 数学广场——周期问题
- 数学广场——流程图(2)
