人教版七年级数学上册 1.2.4 n个绝对值之和的最小值课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.2.4 n个绝对值之和的最小值课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 21:39:15 | ||
图片预览





文档简介
(共20张PPT)
值
最
小
绝
对
值
n
个
之
和
的
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
x
2
x
0
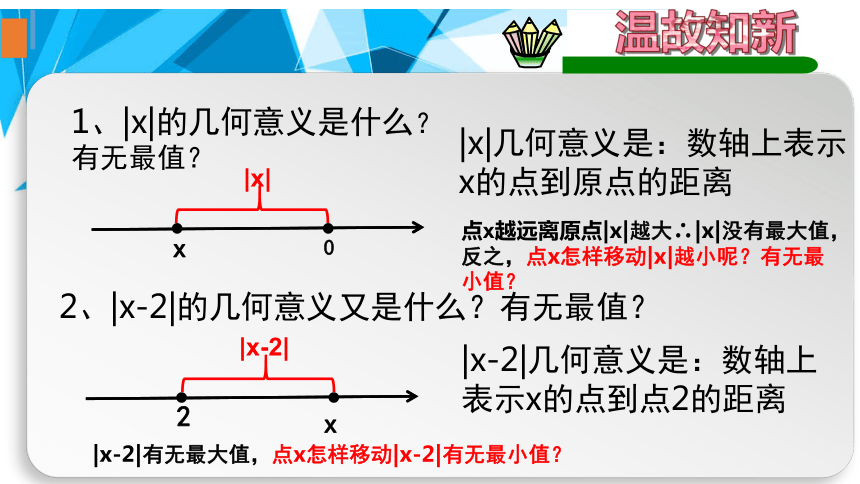
|x|
|x-2|
2、|x-2|的几何意义又是什么?有无最值?
|x|几何意义是:数轴上表示x的点到原点的距离
|x-2|几何意义是:数轴上表示x的点到点2的距离
1、|x|的几何意义是什么?有无最值?
温故知新
点x越远离原点|x|越大∴|x|没有最大值,反之,点x怎样移动|x|越小呢?有无最小值?
|x-2|有无最大值,点x怎样移动|x-2|有无最小值?
x
-2
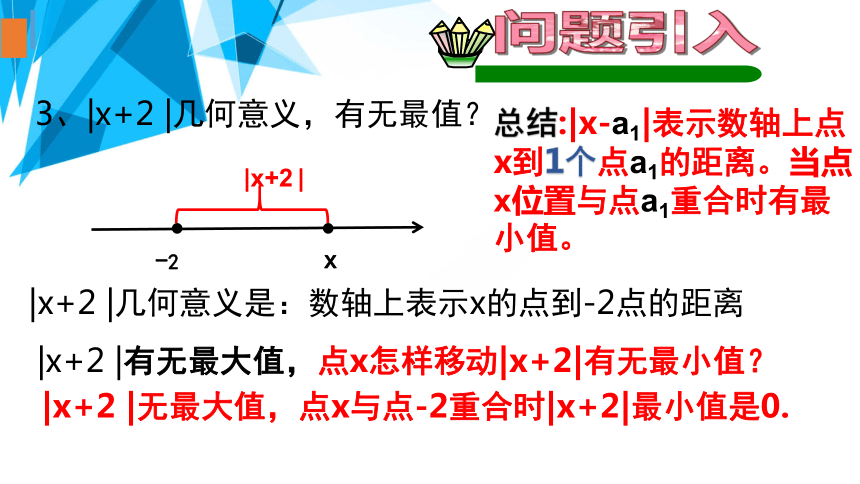
|x+2 |
3、|x+2 |几何意义,有无最值?
|x+2 |几何意义是:数轴上表示x的点到-2点的距离
|x+2 |有无最大值,点x怎样移动|x+2|有无最小值?
|x+2 |无最大值,点x与点-2重合时|x+2|最小值是0.
问题引入
总结:|x-a1|表示数轴上点x到1个点a1的距离。当点x位置与点a1重合时有最小值。
例1:求|x-1|+|x-2|的最小值。
分析:|x-1|+|x-2|几何意义是:数轴上表示x的点到点1,点2的距离和
1
2
x应该处于什么位置距离和最小?是多少?
总结:∣x-a1∣+ ∣x-a2∣表示数轴上点x到2个点的距离和,此时点x位置在两个点之间的线段上最小。最小值是线段的长。
点1,点2把数轴分成了3段
问题加深
A
B
例2:求|x+3|+|x-4|+|x-5|的最小值。
注意:∣x-a1∣+ ∣x-a2∣+ ∣x-a3∣表示数轴上点x到3个点的距离和,当点x位置在中间这个点上(点x与中间点重合)时有最小值。
-3
4
5
x应该处于什么位置距离和最小?是多少?
再探问题
点-3,点4、点5把数轴分成了( )段
一般步骤:
1,分组 2,定位置 3,求和
例2:求|x+3|+|x-4|+|x-5|的最小值。
-3
4
5
再探问题
可分为∣x+3∣ + ∣x-5∣和∣x-4∣两组.
当点x在什么位置时,∣x+3∣ + ∣x-5∣有最小值为( ) .
当点x在什么位置时, ∣x-4∣有最小值是( )
8
0
当X为多少时,可以满足两组同时取最小值呢?
因此,当x=()时, |x+3|+|x-4|+|x-5|有最小值,最小值是( )
4
8
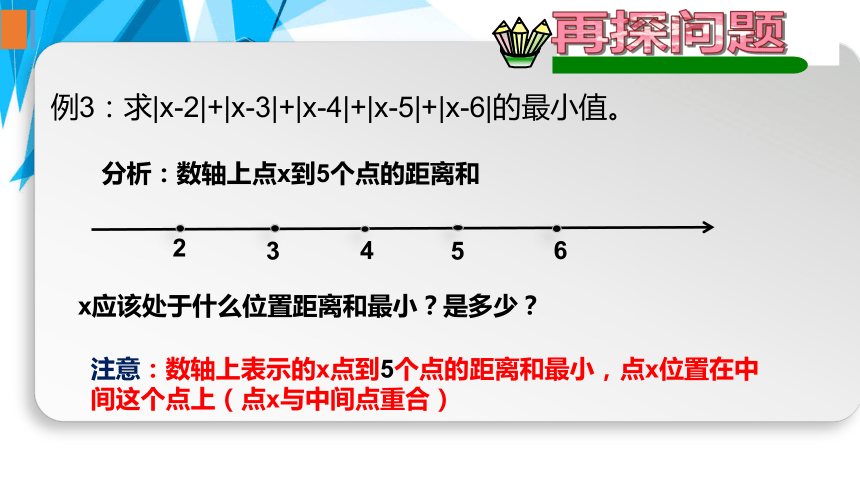
例3:求|x-2|+|x-3|+|x-4|+|x-5|+|x-6|的最小值。
注意:数轴上表示的x点到5个点的距离和最小,点x位置在中间这个点上(点x与中间点重合)
3
4
5
x应该处于什么位置距离和最小?是多少?
再探问题
2
6
分析:数轴上点x到5个点的距离和
例3:求|x-2|+|x-3|+|x-4|+|x-5|+|x-6|的最小值。
再探问题
分析:可分为几组.
当点x在什么位置时,|x-2|和|x-6|有最小值为( ) .
当点x在什么位置时, |x-3|+|x-5|有最小值是( )
4
2
当X为多少时,可以满足两组同时取最小值呢?
因此,当x=()时,|x-2|+|x-3|+|x-4|+|x-5|+|x-6|有最小值,最小值是( )
4
可分为3组.
|x-2|和|x-6|;|x-3|+|x-5|;|x-4|
注意:数轴上表示的x点
到5个点的距离和最小,
点x位置与中间点重合
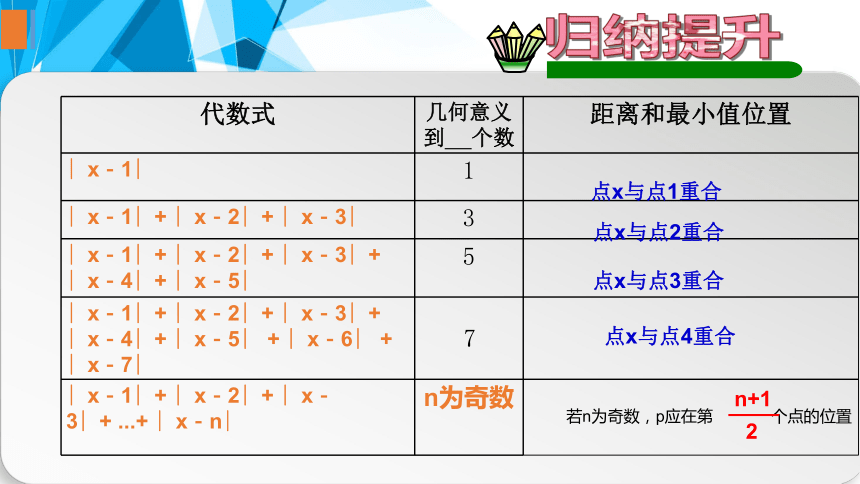
代数式 几何意义
到 个数 距离和最小值位置
∣x-1∣ 1
∣x-1∣+ ∣x-2∣+ ∣x-3∣ 3
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣ 5
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣ + ∣x-6∣ + ∣x-7∣
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
n为奇数
归纳提升
点x与点1重合
点x与点2重合
点x与点3重合
点x与点4重合
若n为奇数,p应在第 个点的位置
n+1
2
7
例1:求|x-1|+|x-2|的最小值。
回顾:x应该处于什么位置距离和最小?
1
2
变式:∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣的最小值
总结:当数轴上点x到2个点的距离和最小,此时点x位置在两个点间的线段上最小。
再探问题2
A
B
?
?
?
?
1
4
2
3
分析:可分为几组.
可分为2组.
∣x-1∣和 ∣x-4∣;∣x-2∣和 ∣x-3∣
总结:当数轴上点x到4个点的距离和最小,此时点x位置在中间两点间的线段上最小。
代数式 几何意义
到 个数 距离和最小值位置
∣x-1∣+ ∣x-2∣ 2
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣ 4
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣+ ∣x-6∣
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
归纳提升
点1,点2间的线段上
点2,点3间的线段上
点3,点4间的线段上
n
2
6
n为
偶数
n
2
若n为偶数,点x在第 个点和 第( +1) 之间的线段上
…
建立模型
一般地,当数轴上有n个点时,在数轴上找到点x,使点x到n个点的距离之和最小,点x应设在 :
若n为奇数,x应设在第 个点的位置;
若n为偶数,x应设在第 个点和第( ) 个点之间的线段上。
2
2
n+1
n
2
n
+1
求n个绝对值之和的最小值问题方法:
归纳提高
四、闯关练习
第一关
闯关练习
四、闯关练习
第一关
根据上述结论,
(1) 求:|x-2| +|x+3|的最小值。
(2) 求:|x+1| +|x+5|+|x-4|的最小值。
(3)求∣x-2∣+ ∣x-4∣+ ∣x-6∣+ ...+ ∣x-398∣的最小值。
闯关练习
…
第二关
某公司员工分别住在A,B,C三个住宅区,A区,B区,C区员工人数分别为:3人,1人,2人。三个小区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点, 为使所有员工步行到停靠点的距离之和最小,那么停靠点应设在( )。
A.A B.B C.C D.A,B之间
A
C
B
闯关练习2
…
四、闯关练习
第二关
…
四、闯关练习
第二关
某公司员工分别住在A,B,C三个住宅区,A区,B区,C区员工人数分别为:3人,1人,2人。三个小区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点, 为使所有员工步行到停靠点的距离之和最小,那么停靠点应设在( )。
A.A B.B C.C D.A,B之间
A
C
B
D
…
建立模型
一般地,当数轴上有n个点时,在数轴上找到点x,使点x到n个点的距离之和最小,点x应设在 :
若n为奇数,x应设在第 个点的位置;
若n为偶数,x应设在第 个点和第( ) 个点之间的线段上。
2
2
n+1
n
2
n
+1
求n个绝对值之和的最小值问题方法:
小结
…
第三关
根据上述结论,
求: 2|x+3| +|x-1|的最小值。
布置作业
谢
谢
指
导
值
最
小
绝
对
值
n
个
之
和
的
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
x
2
x
0
|x|
|x-2|
2、|x-2|的几何意义又是什么?有无最值?
|x|几何意义是:数轴上表示x的点到原点的距离
|x-2|几何意义是:数轴上表示x的点到点2的距离
1、|x|的几何意义是什么?有无最值?
温故知新
点x越远离原点|x|越大∴|x|没有最大值,反之,点x怎样移动|x|越小呢?有无最小值?
|x-2|有无最大值,点x怎样移动|x-2|有无最小值?
x
-2
|x+2 |
3、|x+2 |几何意义,有无最值?
|x+2 |几何意义是:数轴上表示x的点到-2点的距离
|x+2 |有无最大值,点x怎样移动|x+2|有无最小值?
|x+2 |无最大值,点x与点-2重合时|x+2|最小值是0.
问题引入
总结:|x-a1|表示数轴上点x到1个点a1的距离。当点x位置与点a1重合时有最小值。
例1:求|x-1|+|x-2|的最小值。
分析:|x-1|+|x-2|几何意义是:数轴上表示x的点到点1,点2的距离和
1
2
x应该处于什么位置距离和最小?是多少?
总结:∣x-a1∣+ ∣x-a2∣表示数轴上点x到2个点的距离和,此时点x位置在两个点之间的线段上最小。最小值是线段的长。
点1,点2把数轴分成了3段
问题加深
A
B
例2:求|x+3|+|x-4|+|x-5|的最小值。
注意:∣x-a1∣+ ∣x-a2∣+ ∣x-a3∣表示数轴上点x到3个点的距离和,当点x位置在中间这个点上(点x与中间点重合)时有最小值。
-3
4
5
x应该处于什么位置距离和最小?是多少?
再探问题
点-3,点4、点5把数轴分成了( )段
一般步骤:
1,分组 2,定位置 3,求和
例2:求|x+3|+|x-4|+|x-5|的最小值。
-3
4
5
再探问题
可分为∣x+3∣ + ∣x-5∣和∣x-4∣两组.
当点x在什么位置时,∣x+3∣ + ∣x-5∣有最小值为( ) .
当点x在什么位置时, ∣x-4∣有最小值是( )
8
0
当X为多少时,可以满足两组同时取最小值呢?
因此,当x=()时, |x+3|+|x-4|+|x-5|有最小值,最小值是( )
4
8
例3:求|x-2|+|x-3|+|x-4|+|x-5|+|x-6|的最小值。
注意:数轴上表示的x点到5个点的距离和最小,点x位置在中间这个点上(点x与中间点重合)
3
4
5
x应该处于什么位置距离和最小?是多少?
再探问题
2
6
分析:数轴上点x到5个点的距离和
例3:求|x-2|+|x-3|+|x-4|+|x-5|+|x-6|的最小值。
再探问题
分析:可分为几组.
当点x在什么位置时,|x-2|和|x-6|有最小值为( ) .
当点x在什么位置时, |x-3|+|x-5|有最小值是( )
4
2
当X为多少时,可以满足两组同时取最小值呢?
因此,当x=()时,|x-2|+|x-3|+|x-4|+|x-5|+|x-6|有最小值,最小值是( )
4
可分为3组.
|x-2|和|x-6|;|x-3|+|x-5|;|x-4|
注意:数轴上表示的x点
到5个点的距离和最小,
点x位置与中间点重合
代数式 几何意义
到 个数 距离和最小值位置
∣x-1∣ 1
∣x-1∣+ ∣x-2∣+ ∣x-3∣ 3
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣ 5
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣ + ∣x-6∣ + ∣x-7∣
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
n为奇数
归纳提升
点x与点1重合
点x与点2重合
点x与点3重合
点x与点4重合
若n为奇数,p应在第 个点的位置
n+1
2
7
例1:求|x-1|+|x-2|的最小值。
回顾:x应该处于什么位置距离和最小?
1
2
变式:∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣的最小值
总结:当数轴上点x到2个点的距离和最小,此时点x位置在两个点间的线段上最小。
再探问题2
A
B
?
?
?
?
1
4
2
3
分析:可分为几组.
可分为2组.
∣x-1∣和 ∣x-4∣;∣x-2∣和 ∣x-3∣
总结:当数轴上点x到4个点的距离和最小,此时点x位置在中间两点间的线段上最小。
代数式 几何意义
到 个数 距离和最小值位置
∣x-1∣+ ∣x-2∣ 2
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣ 4
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ∣x-4∣+ ∣x-5∣+ ∣x-6∣
∣x-1∣+ ∣x-2∣+ ∣x-3∣+ ...+ ∣x-n∣
归纳提升
点1,点2间的线段上
点2,点3间的线段上
点3,点4间的线段上
n
2
6
n为
偶数
n
2
若n为偶数,点x在第 个点和 第( +1) 之间的线段上
…
建立模型
一般地,当数轴上有n个点时,在数轴上找到点x,使点x到n个点的距离之和最小,点x应设在 :
若n为奇数,x应设在第 个点的位置;
若n为偶数,x应设在第 个点和第( ) 个点之间的线段上。
2
2
n+1
n
2
n
+1
求n个绝对值之和的最小值问题方法:
归纳提高
四、闯关练习
第一关
闯关练习
四、闯关练习
第一关
根据上述结论,
(1) 求:|x-2| +|x+3|的最小值。
(2) 求:|x+1| +|x+5|+|x-4|的最小值。
(3)求∣x-2∣+ ∣x-4∣+ ∣x-6∣+ ...+ ∣x-398∣的最小值。
闯关练习
…
第二关
某公司员工分别住在A,B,C三个住宅区,A区,B区,C区员工人数分别为:3人,1人,2人。三个小区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点, 为使所有员工步行到停靠点的距离之和最小,那么停靠点应设在( )。
A.A B.B C.C D.A,B之间
A
C
B
闯关练习2
…
四、闯关练习
第二关
…
四、闯关练习
第二关
某公司员工分别住在A,B,C三个住宅区,A区,B区,C区员工人数分别为:3人,1人,2人。三个小区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点, 为使所有员工步行到停靠点的距离之和最小,那么停靠点应设在( )。
A.A B.B C.C D.A,B之间
A
C
B
D
…
建立模型
一般地,当数轴上有n个点时,在数轴上找到点x,使点x到n个点的距离之和最小,点x应设在 :
若n为奇数,x应设在第 个点的位置;
若n为偶数,x应设在第 个点和第( ) 个点之间的线段上。
2
2
n+1
n
2
n
+1
求n个绝对值之和的最小值问题方法:
小结
…
第三关
根据上述结论,
求: 2|x+3| +|x-1|的最小值。
布置作业
谢
谢
指
导
