京改版九下 23.4 位似变换 学案(无答案)
文档属性
| 名称 | 京改版九下 23.4 位似变换 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 15.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 09:38:26 | ||
图片预览

文档简介
位似变换
【学习目标】
(一)知识目标:
通过探究得出位似变换的定义和性质;
(二)能力目标:
1.掌握位似图形的画法;
2.掌握位似变换与坐标的关系。
(三)情感目标:
积极参与,全身心投入,享受学习的快乐,做最棒的自己。
【学习重难点】
1.掌握位似图形的画法;
2.掌握位似变换与坐标的关系
【学习过程】
一、导学
位似图形的探究
请你从以下3方面探究这两个相似图形之间存在哪些内在的关系?
这两个相似图形对应点的连线
这两个相似图形对应边
(1)
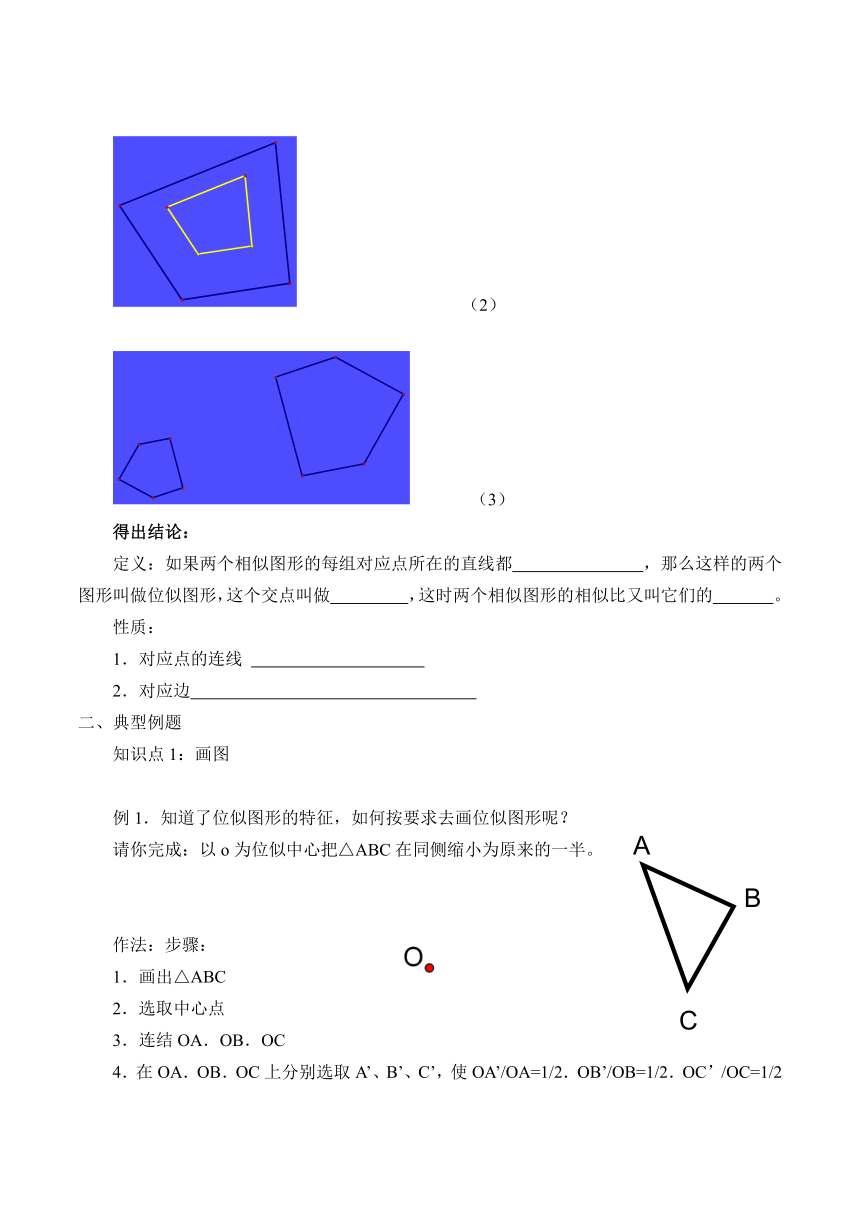
(2)
(3)
得出结论:
定义:如果两个相似图形的每组对应点所在的直线都 ,那么这样的两个图形叫做位似图形,这个交点叫做 ,这时两个相似图形的相似比又叫它们的 。
性质:
1.对应点的连线
2.对应边
二、典型例题
知识点1:画图
例1.知道了位似图形的特征,如何按要求去画位似图形呢?
请你完成:以o为位似中心把△ABC在同侧缩小为原来的一半。
作法:步骤:
1.画出△ABC
2.选取中心点
3.连结OA.OB.OC
4.在OA.OB.OC上分别选取A’、B’、C’,使OA’/OA=1/2.OB’/OB=1/2.OC’/OC=1/2
5.连结A’B’C’,所连成的图形就是所求作图形。
【练习】如图:以O为位似中心,将△ABC放大为原来的两倍(不写作法)
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
知识点2:位似变换与坐标的关系
例2.在平面直角体系中有两点A(6,3)、B(6,0),以原点O为位似中心,相似比为1/3,把线段缩小。观察对应点之间的坐标的变化,你有什么发现?
A′( , ) B′( , )
归纳:
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于
【练习】
1.如果四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),写出以原点为位似中心,相似比为(1/2)的一个图形的对应点的坐标。
2.如图,在直角坐标系中,△ABC的各个顶点的坐标为A(-1,1),B(2,3),C(0,3).现要以坐标原点O为位似中心,位似比为,作△ABC的位似图形△A′B′C′,则它的顶点A′、B′、C′的坐标各是多少?
【学习目标】
(一)知识目标:
通过探究得出位似变换的定义和性质;
(二)能力目标:
1.掌握位似图形的画法;
2.掌握位似变换与坐标的关系。
(三)情感目标:
积极参与,全身心投入,享受学习的快乐,做最棒的自己。
【学习重难点】
1.掌握位似图形的画法;
2.掌握位似变换与坐标的关系
【学习过程】
一、导学
位似图形的探究
请你从以下3方面探究这两个相似图形之间存在哪些内在的关系?
这两个相似图形对应点的连线
这两个相似图形对应边
(1)
(2)
(3)
得出结论:
定义:如果两个相似图形的每组对应点所在的直线都 ,那么这样的两个图形叫做位似图形,这个交点叫做 ,这时两个相似图形的相似比又叫它们的 。
性质:
1.对应点的连线
2.对应边
二、典型例题
知识点1:画图
例1.知道了位似图形的特征,如何按要求去画位似图形呢?
请你完成:以o为位似中心把△ABC在同侧缩小为原来的一半。
作法:步骤:
1.画出△ABC
2.选取中心点
3.连结OA.OB.OC
4.在OA.OB.OC上分别选取A’、B’、C’,使OA’/OA=1/2.OB’/OB=1/2.OC’/OC=1/2
5.连结A’B’C’,所连成的图形就是所求作图形。
【练习】如图:以O为位似中心,将△ABC放大为原来的两倍(不写作法)
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
知识点2:位似变换与坐标的关系
例2.在平面直角体系中有两点A(6,3)、B(6,0),以原点O为位似中心,相似比为1/3,把线段缩小。观察对应点之间的坐标的变化,你有什么发现?
A′( , ) B′( , )
归纳:
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于
【练习】
1.如果四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),写出以原点为位似中心,相似比为(1/2)的一个图形的对应点的坐标。
2.如图,在直角坐标系中,△ABC的各个顶点的坐标为A(-1,1),B(2,3),C(0,3).现要以坐标原点O为位似中心,位似比为,作△ABC的位似图形△A′B′C′,则它的顶点A′、B′、C′的坐标各是多少?
