1.5 三角函数的应用一课一练测试题(含解析)
文档属性
| 名称 | 1.5 三角函数的应用一课一练测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 643.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 12:42:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九下同步课堂【一课一练】(北师大版)
第一章 直角三角形的边角关系
第五节 三角函数的应用
学校:___________姓名:___________班级:___________总分:___________
一.选择题(共8小题)
1.如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )
A.米 B.2sin80°米
C.米 D.2.2cos80°米
2.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为( )
A.12米 B.4米 C.5米 D.6米
3.如图,传送带和地面所成斜坡AB的坡比为1:2,物体沿传送带上升到点B时,距离地面的高度为3米,那么斜坡AB的长度为( )
A.3米 B.5米 C.米 D.6米
4.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. B. C. D.
5.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.7米
6.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
7.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是( )
A.2.7米 B.3.0米 C.3.2米 D.3.4米
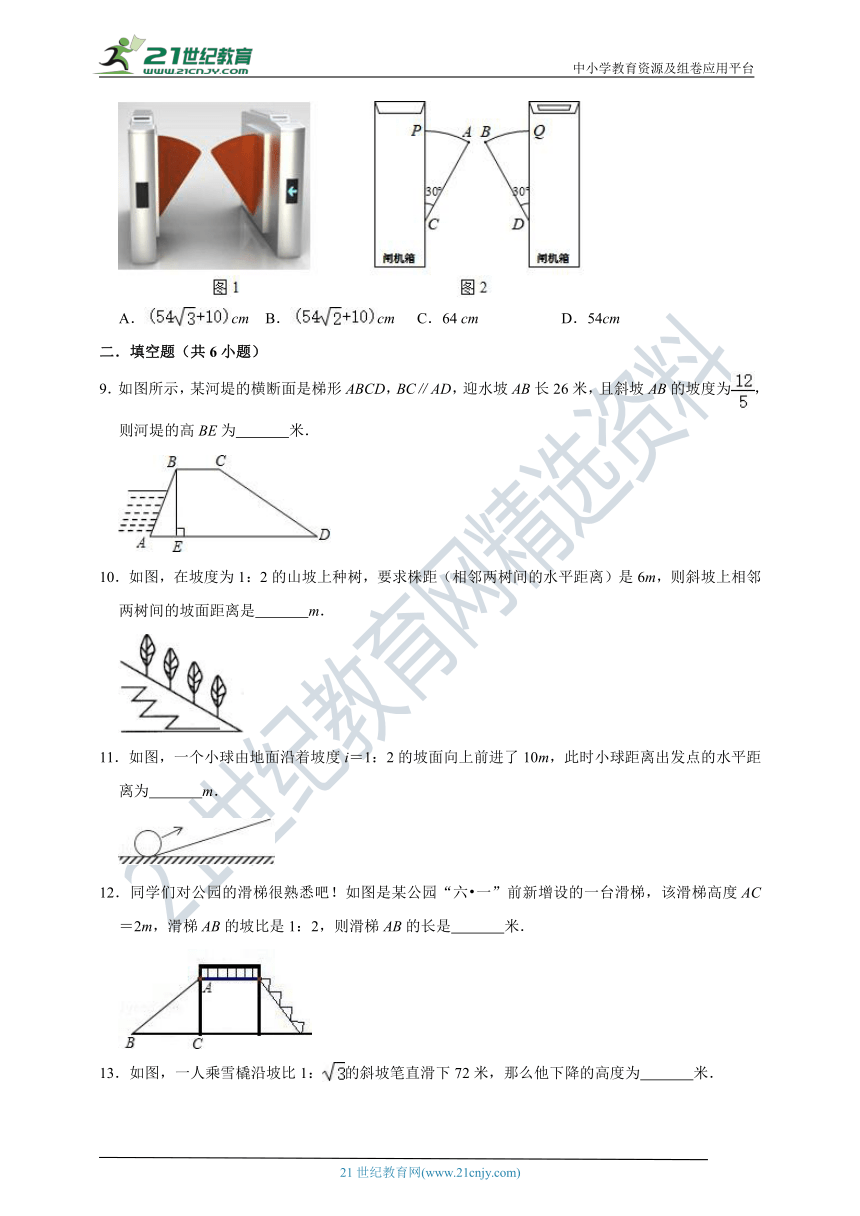
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.cm B.cm C.64 cm D.54cm
二.填空题(共6小题)
9.如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长26米,且斜坡AB的坡度为,则河堤的高BE为 米.
10.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 m.
11.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
12.同学们对公园的滑梯很熟悉吧!如图是某公园“六?一”前新增设的一台滑梯,该滑梯高度AC=2m,滑梯AB的坡比是1:2,则滑梯AB的长是 米.
13.如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米.
14.如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
三.解答题(共5小题)
15.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3米.求点B到地面的垂直距离BC.
16.如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,女生楼在男生楼墙面上的影高为DA.已知CD=42m.求楼间距AB的长度为多少米?(参考数据:sin32.3°=0.53,cos32.3°=0.85,tan32.3°=0.63,sin55.7°=0.83,cos55.7°=0.56,tan55.7°=1.47)
17.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
18.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
19.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
1.5 三角函数的应用
参考答案与试题解析
一.选择题(共8小题)
1.如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )
A.米 B.2sin80°米
C.米 D.2.2cos80°米
【解答】解:∵DA=0.2米,AB=2米,
∴DB=DA+AB=2.2米,
∵光线与地面成80°角,∴∠BCD=80°.
又∵tan∠BCD=,
∴DC==.
故选:C.
2.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为( )
A.12米 B.4米 C.5米 D.6米
【解答】解:∵BC=6米,迎水坡AB的坡比为1:,
∴AC=6(米),
∴AB==12(米).
故选:A.
3.如图,传送带和地面所成斜坡AB的坡比为1:2,物体沿传送带上升到点B时,距离地面的高度为3米,那么斜坡AB的长度为( )
A.3米 B.5米 C.米 D.6米
【解答】解:作BC⊥地面于点C,
设BC=x米,
∵传送带和地面所成斜坡AB的坡度为1:2,
∴AC=2x米,
∵BC=3m,
∴AC=6m,
∴AB==3(m),
故选:A.
4.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. B. C. D.
【解答】解:
∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=,
∴BC==,
故选:B.
5.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.7米
【解答】解:如图AC=13,作CB⊥AB,
∵sinα==,
∴BC=5,
∴小车上升的高度是5m.
故选:A.
6.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
【解答】解:∵斜面坡度为1:2,BC=6m,
∴AC=12m,
则AB=(m).
故选:B.
7.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是( )
A.2.7米 B.3.0米 C.3.2米 D.3.4米
【解答】解:在直角△ADE中,∠DAE=α,AE=5米,tan,
∴tanα===,
∴DE=1.5米.
又CE=AB=1.7米,
∴CD=CE+DE=3.2米.
故选:C.
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.cm B.cm C.64 cm D.54cm
【解答】解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则
Rt△ACE中,AE=AC=×54=27(cm),
同理可得,BF=27cm,
又∵点A与B之间的距离为10cm,
∴通过闸机的物体的最大宽度为27+10+27=64(cm),
故选:C.
二.填空题(共6小题)
9.如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长26米,且斜坡AB的坡度为,则河堤的高BE为 24 米.
【解答】解:由已知斜坡AB的坡度,得:
BE:AE=12:5,
设AE=5x,则BE=12x,
在直角三角形AEB中,根据勾股定理得:
262=5x2+(12x)2,
即169x2=676,
解得:x=2或x=﹣2(舍去),
5x=10,12x=24
即河堤高BE等于24米.
故答案为:24.
10.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 3 m.
【解答】解:∵坡度为1:2,=,且株距为6米,
∴株距:坡面距离=2:,
∴坡面距离=株距×=3(米).
另解:∵CB:AB=1:2,
设CB=x,AB=2x,
∴AC==x,
∴=,
∵AB=6m,
∴AC=×6=3m.
故答案为:3.
11.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
【解答】解:∵AB=10米,tanA==.
∴设BC=x,AC=2x,
由勾股定理得,AB2=AC2+BC2,即100=x2+4x2,解得x=2,
∴AC=4,BC=2米.
故答案为4.
12.同学们对公园的滑梯很熟悉吧!如图是某公园“六?一”前新增设的一台滑梯,该滑梯高度AC=2m,滑梯AB的坡比是1:2,则滑梯AB的长是 米.
【解答】解:由题意知,AC:BC=1;2,且AC=2,故BC=4.
在Rt△ABC中,,
即滑梯AB的长度为米.
13.如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 36 米.
【解答】解:因为坡度比为1:,即tanα=,
∴α=30°.
则其下降的高度=72×sin30°=36(米).
14.如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 8.1 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
【解答】解:如图:AC=3.1m,∠B=38°,
∴AB==,
∴木杆折断之前高度=AC+AB=3.1+5=8.1(m)
故答案为8.1
三.解答题(共5小题)
15.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3米.求点B到地面的垂直距离BC.
【解答】解:在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,AE=DE=3.
∴AD2=AE2+DE2=(3)2+(3)2=36,
∴AD=6,即梯子的总长为6米.
∴AB=AD=6.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC=AB=3,
∴BC2=AB2﹣AC2=62﹣32=27,
∴BC==3m,
∴点B到地面的垂直距离BC=3m.
16.如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,女生楼在男生楼墙面上的影高为DA.已知CD=42m.求楼间距AB的长度为多少米?(参考数据:sin32.3°=0.53,cos32.3°=0.85,tan32.3°=0.63,sin55.7°=0.83,cos55.7°=0.56,tan55.7°=1.47)
【解答】解:如图,作CM⊥BE于M,DN⊥BE于N.则四边形CDNM是矩形,设EM=xm,AB=DN=CM=ym.
在Rt△CEM中,∵tan∠ECM==0.63,
∴=0.63 ①,
在Rt△DEN中,∵tan∠EDN==1.47,
∴=1.47 ②,
由①②可得y=50,
答:楼间距AB的长度为50m.
17.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
【解答】解:∵AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△FAB∽△FDE,
∴=,
∵FB=4米,BE=6米,DE=9米,
∴=,得AB=3.6米,
∵∠ABC=90°,∠BAC=53°,cos∠BAC=,
∴AC===6米,
∴AB+AC=3.6+6=9.6米,
即这棵大树没有折断前的高度是9.6米.
18.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
【解答】解:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,
∴AE=18米,
在RT△ADE中,AD==6米
∵背水坡坡比为1:2,
∴BF=60米,
在RT△BCF中,BC==30米,
∴周长=DC+AD+AE+EF+BF+BC=6+10+30+88=(6+30+98)米,
面积=(10+18+10+60)×30÷2=1470(平方米).
故大坝的截面的周长是(6+30+98)米,面积是1470平方米.
19.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
【解答】解:(1)在Rt△DCB中,sin∠DCB==,
∴设DB=4x,DC=5x,
∴(4x)2+25=(5x)2,
解得,
∴CD=米,DB=米.
(2)如图,过点E作EF⊥AB于点F.
∵∠EAB=120°,∴∠EAF=60°,
∴AF=AE?cos∠EAF=1.6×=0.8(米),
∴FB=AF+AD+DB=0.8+2+=(米).
∴灯的顶端E距离地面米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
