人教版2020八年级数学下册18.2.3正方形同步练习含答案
文档属性
| 名称 | 人教版2020八年级数学下册18.2.3正方形同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 391.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 13:01:34 | ||
图片预览




文档简介
18.2.3 正方形
知识要点:
1.性质:①四条边都相等;
②四个角都是90°;
③对角线相等且互相垂直平分;
④每条对角线平分一组对角;
⑤正方形的中点四边形是正方形;
⑥矩形四个角平分线所成的四边形是正方形
2.判定:①四边相等,有三个角是直角的四边形是正方形;
②一组邻边相等的矩形是正方形;
③一组邻边相等且有一个角是直角的平行四边形是正方形;
④有一个角是直角的菱形是正方形;
⑤对角线相等的菱形是正方形;
⑥对角线互相垂直的矩形是正方形
一、单选题
1.正方形有而矩形不一定有的性质是( )
A.四个角都是直角 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
2.如图,从正方形纸片的顶点沿虚线剪开,则∠1的度数可能是( )
A.44 B.45 C.46 D.47
3.如图,在正方形ABCD中,点E在边BC上,点F在线段DE上,若AB=AF,则∠BFE=( )
A.45° B.30° C.60° D.55°
4.下列叙述,错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
5.在四边形中,,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A. B. C. D.
6.边长为1的正方形的对角线长是( )
A.整数 B.分数 C.有理数 D.无理数
7.如图是边长为的正方形纸片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:)不正确的是( )
A. B. C. D.
8.面积为9㎝2的正方形以对角线为边长的正方形面积为( )
A.18㎝2 B.20㎝2 C.24㎝2 D.28㎝2
9.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中有正确有( )个.
A.2 B.3 C.4 D.5
10.如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABDC的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BC A′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3或7.其中正确的是( )
A.①②③④ B.①③④ C.①②④ D.①②③
二、填空题
11.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于 _________ .
12.如图,将一边长为的正方形纸片的顶点折叠至边上的点,使,折痕为,则的长__________.
13.如图,正方形ABCD的边长为2,顶点A在y轴上,顶点B在x轴上,则OD的最大值是___.
14.已知矩形,给出三个关系式:①②③如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________ .
三、解答题
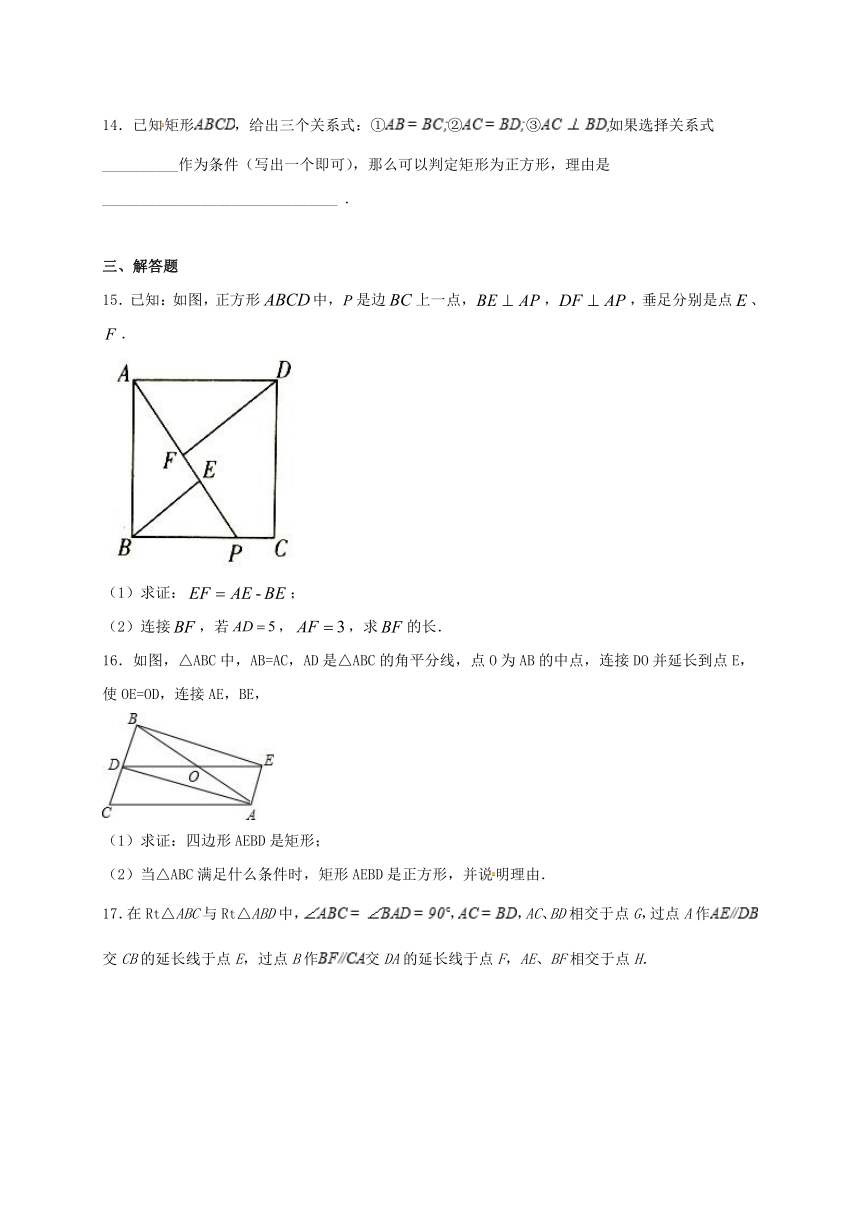
15.已知:如图,正方形中,是边上一点,,,垂足分别是点、.
(1)求证:;
(2)连接,若,,求的长.
16.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
17.在Rt△ABC与Rt△ABD中,,,AC、BD相交于点G,过点A作交CB的延长线于点E,过点B作交DA的延长线于点F,AE、BF相交于点H.
(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
18.探究问题:
⑴方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
⑵方法迁移:
如图②,将沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
答案
1.D
2.A
3.A
4.D
5.A
6.D
7.D
8.A
9.D
10.A
11.22.5°
12.13
13.
14.① 一组邻边相等的矩形是正方形
15.证明:(1)四边形为正方形,
,,
,,
,
,,
,
在和中
,
,
,
;
(2),
,,
,,
,
,
.
16.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
17.解:(1),,
∴Rt△ABC≌Rt△BAD(HL).
(2),,
∴四边形AHBG是平行四边形.
∵△ABC≌Rt△BAD,
,
,
∴平行四边形AHBG是菱形.
(3),,
是等腰直角三角形,
,
又∵△ABC≌△BAD,
,
,
∴菱形AHBG是正方形.
18.⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
假设∠BAD的度数为,将△ADE绕点A顺时针旋转得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=
∴∠2+∠3=∠BAD-∠EAF=
∵∠1=∠2,
∴∠1+∠3=.
即∠GAF=∠EAF
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF
∴DE+BF=EF.
⑶当∠B与∠D互补时,可使得DE+BF=EF
知识要点:
1.性质:①四条边都相等;
②四个角都是90°;
③对角线相等且互相垂直平分;
④每条对角线平分一组对角;
⑤正方形的中点四边形是正方形;
⑥矩形四个角平分线所成的四边形是正方形
2.判定:①四边相等,有三个角是直角的四边形是正方形;
②一组邻边相等的矩形是正方形;
③一组邻边相等且有一个角是直角的平行四边形是正方形;
④有一个角是直角的菱形是正方形;
⑤对角线相等的菱形是正方形;
⑥对角线互相垂直的矩形是正方形
一、单选题
1.正方形有而矩形不一定有的性质是( )
A.四个角都是直角 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
2.如图,从正方形纸片的顶点沿虚线剪开,则∠1的度数可能是( )
A.44 B.45 C.46 D.47
3.如图,在正方形ABCD中,点E在边BC上,点F在线段DE上,若AB=AF,则∠BFE=( )
A.45° B.30° C.60° D.55°
4.下列叙述,错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
5.在四边形中,,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A. B. C. D.
6.边长为1的正方形的对角线长是( )
A.整数 B.分数 C.有理数 D.无理数
7.如图是边长为的正方形纸片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:)不正确的是( )
A. B. C. D.
8.面积为9㎝2的正方形以对角线为边长的正方形面积为( )
A.18㎝2 B.20㎝2 C.24㎝2 D.28㎝2
9.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中有正确有( )个.
A.2 B.3 C.4 D.5
10.如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABDC的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BC A′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3或7.其中正确的是( )
A.①②③④ B.①③④ C.①②④ D.①②③
二、填空题
11.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于 _________ .
12.如图,将一边长为的正方形纸片的顶点折叠至边上的点,使,折痕为,则的长__________.
13.如图,正方形ABCD的边长为2,顶点A在y轴上,顶点B在x轴上,则OD的最大值是___.
14.已知矩形,给出三个关系式:①②③如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________ .
三、解答题
15.已知:如图,正方形中,是边上一点,,,垂足分别是点、.
(1)求证:;
(2)连接,若,,求的长.
16.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
17.在Rt△ABC与Rt△ABD中,,,AC、BD相交于点G,过点A作交CB的延长线于点E,过点B作交DA的延长线于点F,AE、BF相交于点H.
(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
18.探究问题:
⑴方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
⑵方法迁移:
如图②,将沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
答案
1.D
2.A
3.A
4.D
5.A
6.D
7.D
8.A
9.D
10.A
11.22.5°
12.13
13.
14.① 一组邻边相等的矩形是正方形
15.证明:(1)四边形为正方形,
,,
,,
,
,,
,
在和中
,
,
,
;
(2),
,,
,,
,
,
.
16.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
17.解:(1),,
∴Rt△ABC≌Rt△BAD(HL).
(2),,
∴四边形AHBG是平行四边形.
∵△ABC≌Rt△BAD,
,
,
∴平行四边形AHBG是菱形.
(3),,
是等腰直角三角形,
,
又∵△ABC≌△BAD,
,
,
∴菱形AHBG是正方形.
18.⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
假设∠BAD的度数为,将△ADE绕点A顺时针旋转得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=
∴∠2+∠3=∠BAD-∠EAF=
∵∠1=∠2,
∴∠1+∠3=.
即∠GAF=∠EAF
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF
∴DE+BF=EF.
⑶当∠B与∠D互补时,可使得DE+BF=EF
