人教版2020八年级数学下册18.2.1矩形同步练习含答案
文档属性
| 名称 | 人教版2020八年级数学下册18.2.1矩形同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 490.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 13:04:57 | ||
图片预览

文档简介
18.2.1矩形
知识要点:
1. 性质:
①边——两组对边分别平行且相等;
②角——每个角都是90°;
③对角线——两条对角线相等且互相平分
2. 判定:
①有一个角是90°的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角90°的四边形是矩形
一、单选题
1.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
2.如图,在矩形ABCD中,AC=4,AB=2,则BC的长是( )
A.8 B.4 C.2 D.6
3.在△ABC中,若AB=8,BC=15,AC=17,则AC边上的中线BD的长为( )
A.8 B.8.5 C.9 D.9.5
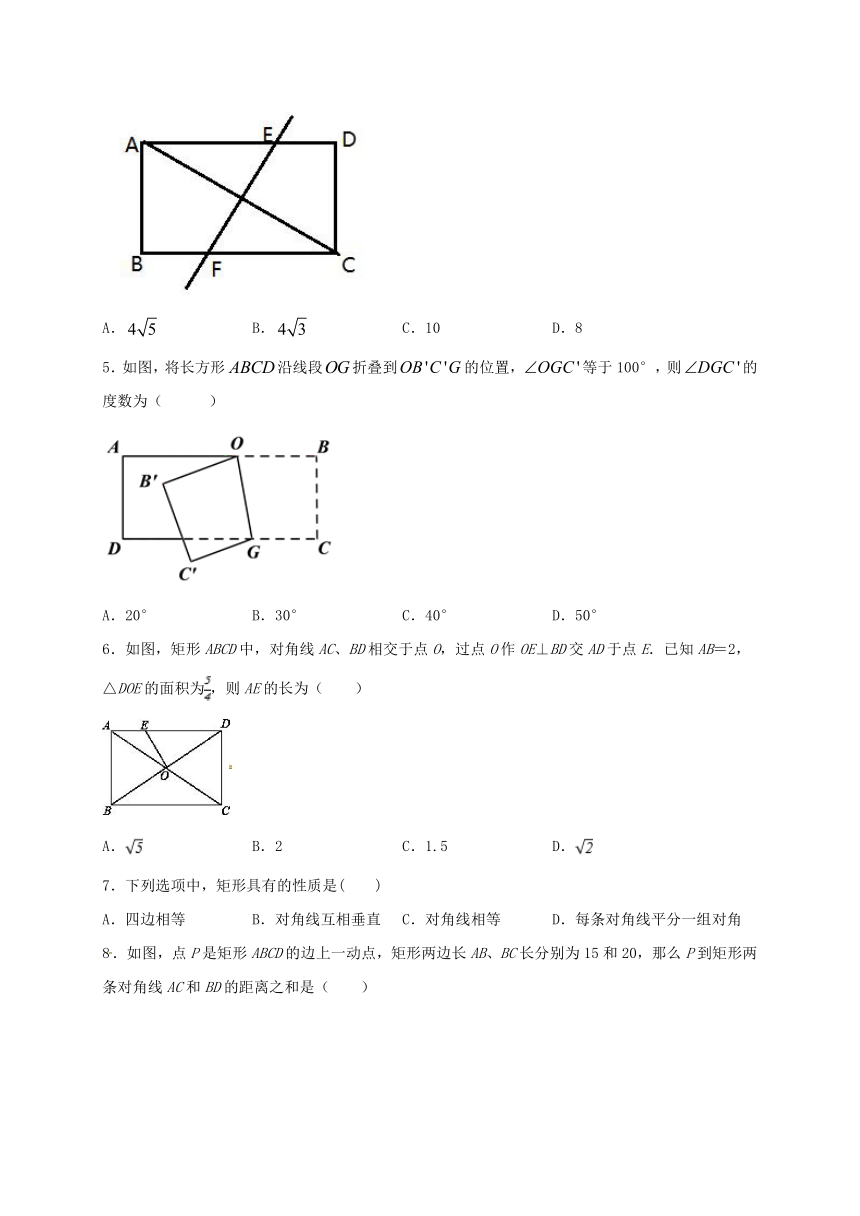
4.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A. B. C.10 D.8
5.如图,将长方形沿线段折叠到的位置,等于100°,则的度数为( )
A.20° B.30° C.40° D.50°
6.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为,则AE的长为( )
A. B.2 C.1.5 D.
7.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
8.如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
A.6 B.12 C.24 D.不能确定
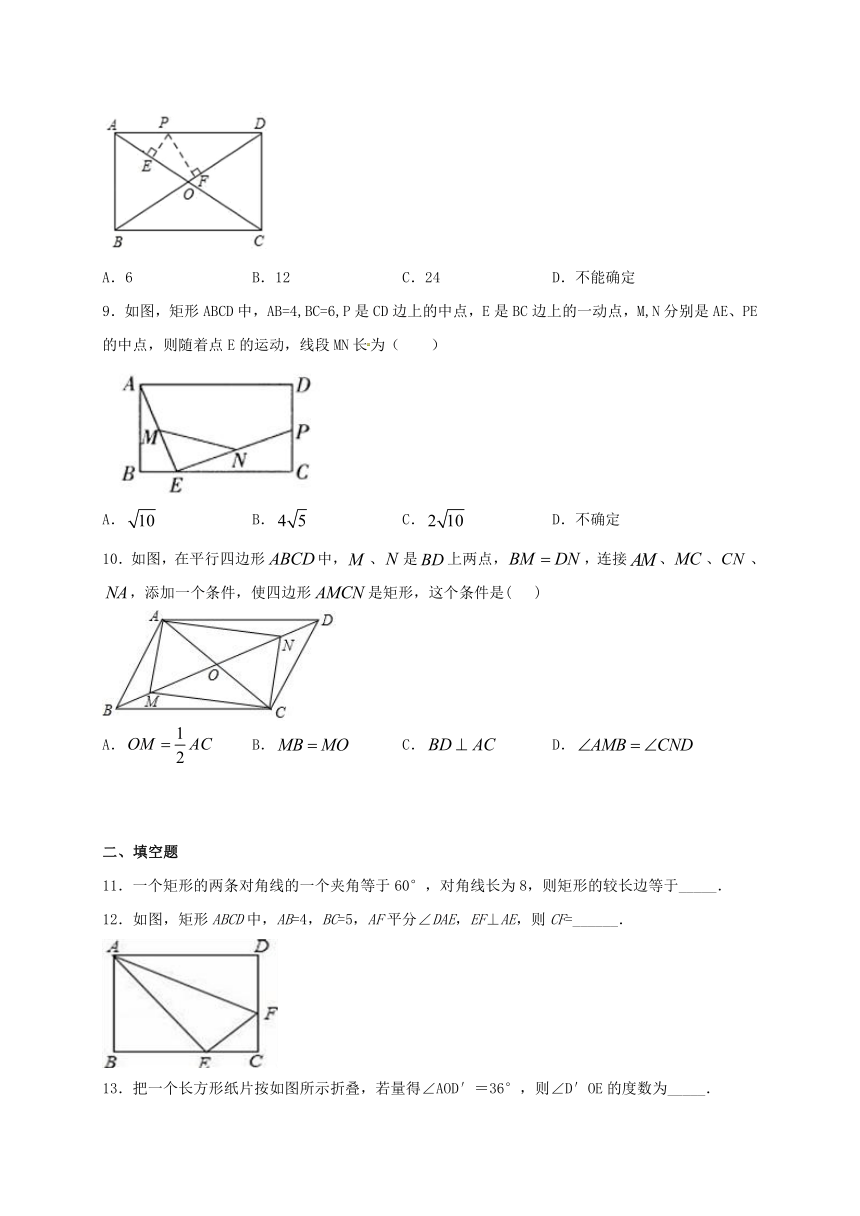
9.如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
A. B. C. D.不确定
10.如图,在平行四边形中,、是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是( )
A. B. C. D.
二、填空题
11.一个矩形的两条对角线的一个夹角等于60°,对角线长为8,则矩形的较长边等于_____.
12.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF=______.
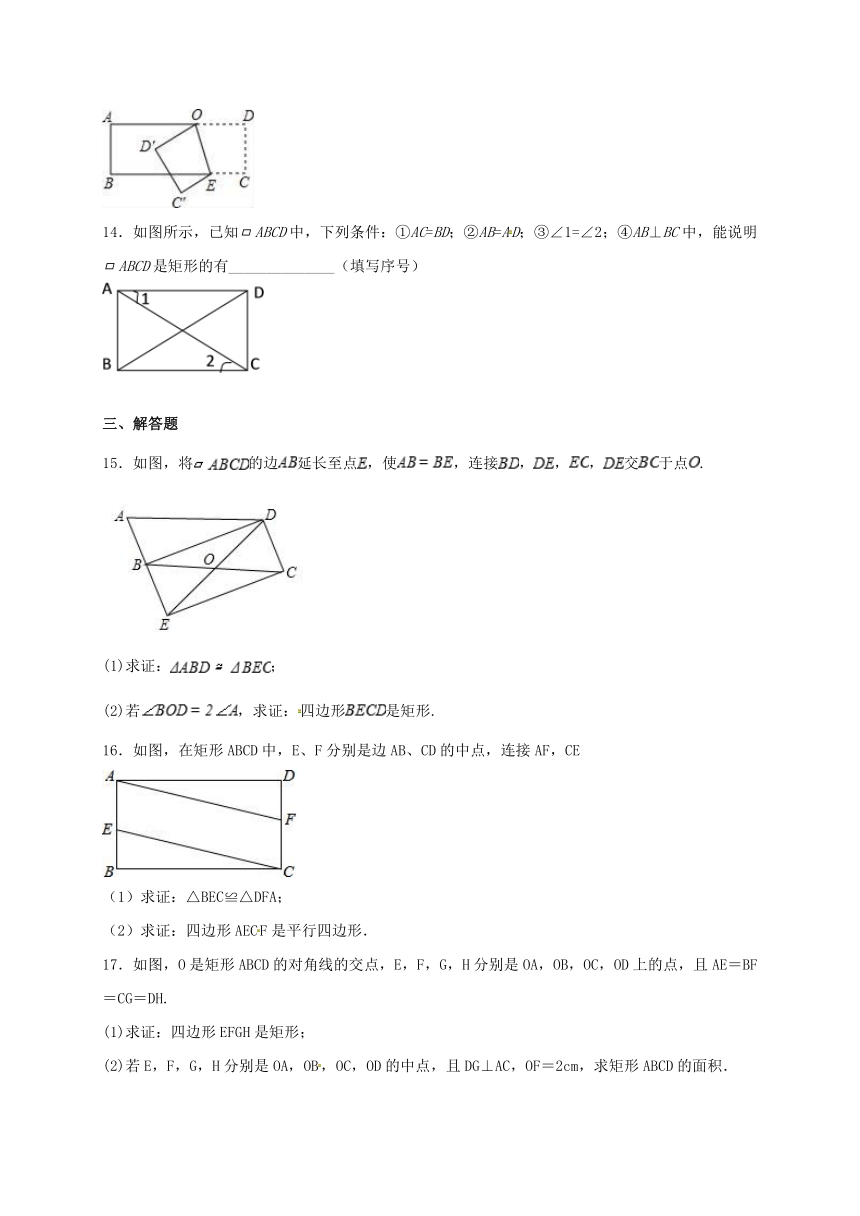
13.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为_____.
14.如图所示,已知ABCD中,下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC中,能说明ABCD是矩形的有______________(填写序号)
三、解答题
15.如图,将的边延长至点,使,连接,,,交于点.
(1)求证:;
(2)若,求证:四边形是矩形.
16.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE
(1)求证:△BEC≌△DFA;
(2)求证:四边形AECF是平行四边形.
17.如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
18.已知:如图,长方形中,,,点是边的中点,点从点出发,以1m/s的速度沿着方向运动再过点沿方向运动,到点停止运动,点以同样的速度从点出发沿着方向运动,到点停止运动,设点运动的路程为.
(1)当时,线段的长是 ;
(2)当点在线段上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
(3)在点的运动过程中,是否存在某一时刻,使得?若存在,求出点的运动路程,若不存在,请说明理由.
答案
1.C
2.C
3.B
4.A
5.A
6.C
7.C
8.B
9.A
10.A
11.4
12.
13.72°
14.①④
15.(1)∵四边形是平行四边形,
∴,
∴.
又∵,
∴.
∴四边形为平行四边形.
∴.
∵在与中,,
∴.
(2)由(1)知,四边形为平行四边形,则.
∵四边形为平行四边形,
∴,即.
又∵,
∴,
∴,
∴,即,
∴四边形是矩形.
16.证明:(1)∵四边形ABCD是矩形,∴AB=CD,AD=BC.
又∵E、F分别是边AB、CD的中点,∴BE=DF.
∵在△BEC和△DFA中,,
∴△BEC≌△DFA(SAS).
(2)由(1)△BEC≌△DFA,
∴CE=AF,
∵E、F分别是边AB、CD的中点,
∴AE=CF
∴四边形AECF是平行四边形.
17.证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
解:∵G是OC的中点,
∴GO=GC.
又∵DG⊥AC,
∴CD=OD.
∵F是BO中点,OF=2cm,
∴BO=4cm.
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB==4 (cm),
∴矩形ABCD的面积为4×4=16 (cm2).
18.(1)∵四边形ABCD是矩形,∴AD=BC=8.
AP=DQ=2,∴AQ=AD﹣DQ=8﹣2=6.
故答案为6.
(2)结论:阴影部分的面积不会发生改变.理由如下:
连结AM,作MH⊥AD于H.则四边形ABMH是矩形,MH=AB=4.
∵S阴=S△APM+S△AQMx×4(8﹣x)×4=16,∴阴影面积不变.
(3)分两种情况讨论:
①当点P在线段AB上时,BP=4﹣x,DQ=x.
∵BPDQ,∴4﹣xx,∴x=3.
②当点P在线段BM上时,BP=x﹣4,DQ=x.
∵BPDQ,∴x﹣4x,∴x=6.
综上所述:当x=3或6时,BPDQ
知识要点:
1. 性质:
①边——两组对边分别平行且相等;
②角——每个角都是90°;
③对角线——两条对角线相等且互相平分
2. 判定:
①有一个角是90°的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角90°的四边形是矩形
一、单选题
1.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
2.如图,在矩形ABCD中,AC=4,AB=2,则BC的长是( )
A.8 B.4 C.2 D.6
3.在△ABC中,若AB=8,BC=15,AC=17,则AC边上的中线BD的长为( )
A.8 B.8.5 C.9 D.9.5
4.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A. B. C.10 D.8
5.如图,将长方形沿线段折叠到的位置,等于100°,则的度数为( )
A.20° B.30° C.40° D.50°
6.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为,则AE的长为( )
A. B.2 C.1.5 D.
7.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
8.如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
A.6 B.12 C.24 D.不能确定
9.如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
A. B. C. D.不确定
10.如图,在平行四边形中,、是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是( )
A. B. C. D.
二、填空题
11.一个矩形的两条对角线的一个夹角等于60°,对角线长为8,则矩形的较长边等于_____.
12.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF=______.
13.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为_____.
14.如图所示,已知ABCD中,下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC中,能说明ABCD是矩形的有______________(填写序号)
三、解答题
15.如图,将的边延长至点,使,连接,,,交于点.
(1)求证:;
(2)若,求证:四边形是矩形.
16.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE
(1)求证:△BEC≌△DFA;
(2)求证:四边形AECF是平行四边形.
17.如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
18.已知:如图,长方形中,,,点是边的中点,点从点出发,以1m/s的速度沿着方向运动再过点沿方向运动,到点停止运动,点以同样的速度从点出发沿着方向运动,到点停止运动,设点运动的路程为.
(1)当时,线段的长是 ;
(2)当点在线段上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
(3)在点的运动过程中,是否存在某一时刻,使得?若存在,求出点的运动路程,若不存在,请说明理由.
答案
1.C
2.C
3.B
4.A
5.A
6.C
7.C
8.B
9.A
10.A
11.4
12.
13.72°
14.①④
15.(1)∵四边形是平行四边形,
∴,
∴.
又∵,
∴.
∴四边形为平行四边形.
∴.
∵在与中,,
∴.
(2)由(1)知,四边形为平行四边形,则.
∵四边形为平行四边形,
∴,即.
又∵,
∴,
∴,
∴,即,
∴四边形是矩形.
16.证明:(1)∵四边形ABCD是矩形,∴AB=CD,AD=BC.
又∵E、F分别是边AB、CD的中点,∴BE=DF.
∵在△BEC和△DFA中,,
∴△BEC≌△DFA(SAS).
(2)由(1)△BEC≌△DFA,
∴CE=AF,
∵E、F分别是边AB、CD的中点,
∴AE=CF
∴四边形AECF是平行四边形.
17.证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
解:∵G是OC的中点,
∴GO=GC.
又∵DG⊥AC,
∴CD=OD.
∵F是BO中点,OF=2cm,
∴BO=4cm.
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB==4 (cm),
∴矩形ABCD的面积为4×4=16 (cm2).
18.(1)∵四边形ABCD是矩形,∴AD=BC=8.
AP=DQ=2,∴AQ=AD﹣DQ=8﹣2=6.
故答案为6.
(2)结论:阴影部分的面积不会发生改变.理由如下:
连结AM,作MH⊥AD于H.则四边形ABMH是矩形,MH=AB=4.
∵S阴=S△APM+S△AQMx×4(8﹣x)×4=16,∴阴影面积不变.
(3)分两种情况讨论:
①当点P在线段AB上时,BP=4﹣x,DQ=x.
∵BPDQ,∴4﹣xx,∴x=3.
②当点P在线段BM上时,BP=x﹣4,DQ=x.
∵BPDQ,∴x﹣4x,∴x=6.
综上所述:当x=3或6时,BPDQ
