人教版2020八年级数学下册17.2勾股逆定理同步练习含答案
文档属性
| 名称 | 人教版2020八年级数学下册17.2勾股逆定理同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 445.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 00:00:00 | ||
图片预览



文档简介
17.2 勾股逆定理
知识要点:
1.勾股定理逆定理:三角形中两边的平方之和等于第三边的平方,这个三角形为直角三角形.
2. 勾股数:
若三个正整数a,b,c满足a?+b?=c?,则称a,b,c是勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;7,24,25;9,40,41……
(1)设n为正整数,由a=2n+1,b=2n(n+1),c=2n(n+1)+1,可得许多组互质的勾股数;
(2)设n为不小于4的偶数,由a=2n,b=n2-1,c= n2+1,可得许多组互质的勾股数
一、单选题
1.下列各组数中,不能构成直角三角形的是( )
A.a=1,b=,c= B.a=5,b=12,c=13 C.a=1,b=,c= D.a=1,b=1,c=2
2.设△ABC的三边分别为a,b,c,满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=90° B.b2=a2-c2
C.∠A:∠B:∠C=3:4:5 D.a:b:c=5:12:13
3.若△ABC的三边满足,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰三角形或直角三角形
4.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
5.如图,在单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
6.下列是勾股数的有( )
① 3、4、5;② 5、12 、13;③ 9、40 、41;④ 13、14、15;⑤;⑥ 11 、60 、61
A.6组 B.5组 C.4组 D.3组
7.如图,四边形ABCD中,AB=4cm, BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
A.6cm2 B.30cm2 C.24cm2 D.72cm2
8.我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米 B.7.5平方千米 C.15平方千米 D.30平方千米
9.如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
A.南偏东30° B.北偏东30° C.南偏东 60° D.南偏西 60°
10.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
二、填空题
11.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______.
12.如图,已知图中小正方形在格点上,则△ABC的面积为__________.
13.如图,在四边形ABCD中,,,,,AB⊥BC,四边形ABCD的面积为___________________.
14.若一个三角形的三边长之比为5∶12∶13,且周长为60 cm,则它的面积为________ cm2.
三、解答题
15.已知:如图,在四边形ABCD中,AB=BC,AD2+CD2=2AB2,CD⊥AD.
(1)求证:AB⊥BC.
(2)若AB=3CD,AD=17,求四边形ABCD的周长.
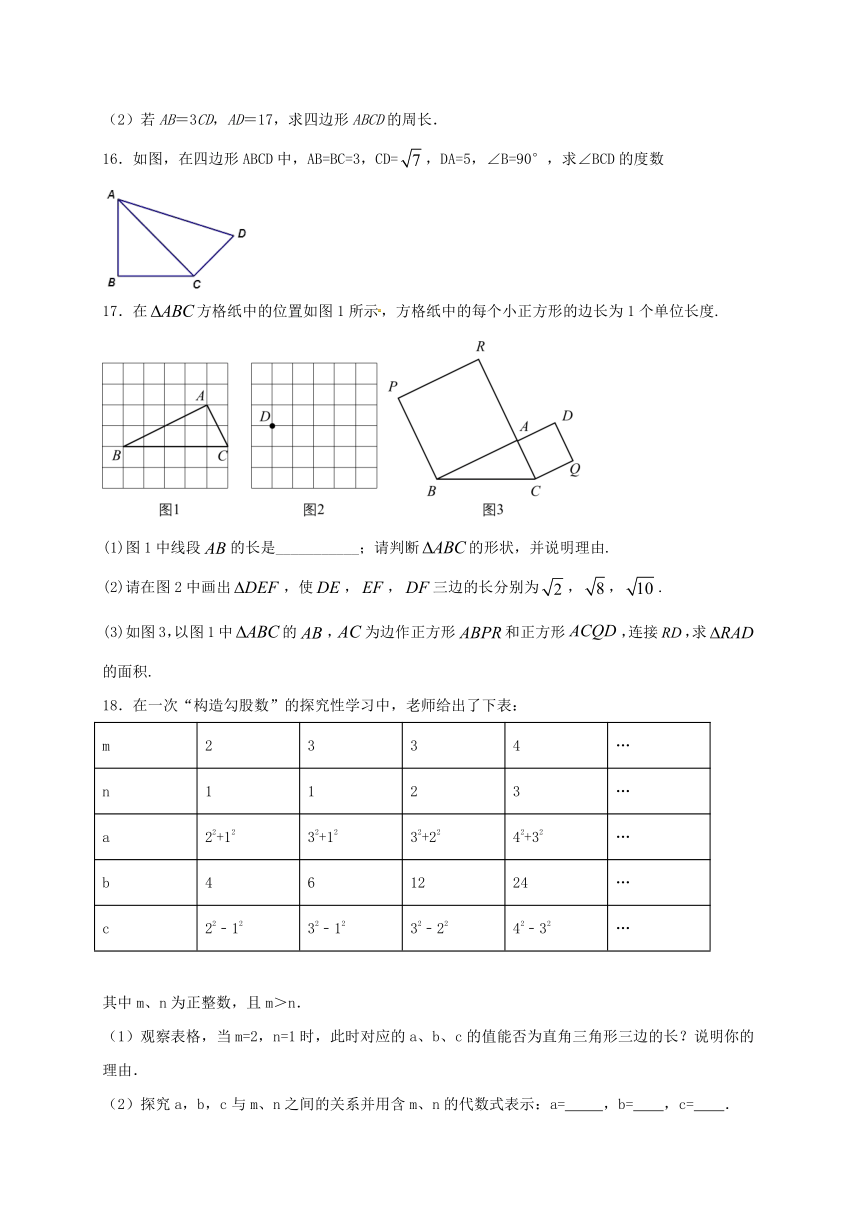
16.如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,求∠BCD的度数
17.在方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
(1)图1中线段的长是___________;请判断的形状,并说明理由.
(2)请在图2中画出,使,,三边的长分别为,,.
(3)如图3,以图1中的,为边作正方形和正方形,连接,求的面积.
18.在一次“构造勾股数”的探究性学习中,老师给出了下表:
m 2 3 3 4 …
n 1 1 2 3 …
a 22+12 32+12 32+22 42+32 …
b 4 6 12 24 …
c 22﹣12 32﹣12 32﹣22 42﹣32 …
其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a= ,b= ,c= .
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例
答案
1.D
2.C
3.D
4.D
5.C
6.C
7.C
8.B
9.C
10.B
11.17,144,145
12.5
13.
14.120
15.(1)证明:连接AC.
∵CD⊥AD,
∴AD2+CD2=AC2,
∵AD2+CD2=2AB2,AB=BC,
∴AC2=AB2+BC2,
∴∠ABC=90°,
∴AB⊥BC.
(2)设CD=k,则AB=BC=3k,
∵∠ABC=90°,
∴AC2=18k2,
在Rt△ACD中,∵AC2=CD2+AD2,
∴18k2=172+k2,
∴k=,
∴CD=,AB=BC=3,
∴四边形ABCD的周长=AB+BC+AD+CD=17+7.
16.解:∵∠B=90°,AB=BC=3,
∴AC===3 ,,∠BAC=∠BCA=45°,
又∵CD=,DA=5,
∴AC2+CD2=18+7=25,AD2=25,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴∠ACD=90°,
∴∠BCD=∠BCA+∠DCA=45°+90°=135°.
17.解:(1)AB=,△ABC为直角三角形,
理由是:AB==,AC==,BC=5,
∵,
∴△ABC为直角三角形;
(2)如图,即为所画三角形:
(3)∵∠BAC=90°,∠BAR=∠CAD=90°,
∴∠RAD=90°,
∵ AR=AB=,AD=AC=,
∴=5.
18.解:(1)当m=2,n=1时,a=5、b=4、c=3,
∵32+42=52,
∴a、b、c的值能为直角三角形三边的长;
(2)观察得,a=m2+n2,b=2mn,c=m2﹣n2;
(3)以a,b,c为边长的三角形一定为直角三角形,
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形
知识要点:
1.勾股定理逆定理:三角形中两边的平方之和等于第三边的平方,这个三角形为直角三角形.
2. 勾股数:
若三个正整数a,b,c满足a?+b?=c?,则称a,b,c是勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;7,24,25;9,40,41……
(1)设n为正整数,由a=2n+1,b=2n(n+1),c=2n(n+1)+1,可得许多组互质的勾股数;
(2)设n为不小于4的偶数,由a=2n,b=n2-1,c= n2+1,可得许多组互质的勾股数
一、单选题
1.下列各组数中,不能构成直角三角形的是( )
A.a=1,b=,c= B.a=5,b=12,c=13 C.a=1,b=,c= D.a=1,b=1,c=2
2.设△ABC的三边分别为a,b,c,满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=90° B.b2=a2-c2
C.∠A:∠B:∠C=3:4:5 D.a:b:c=5:12:13
3.若△ABC的三边满足,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰三角形或直角三角形
4.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
5.如图,在单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
6.下列是勾股数的有( )
① 3、4、5;② 5、12 、13;③ 9、40 、41;④ 13、14、15;⑤;⑥ 11 、60 、61
A.6组 B.5组 C.4组 D.3组
7.如图,四边形ABCD中,AB=4cm, BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
A.6cm2 B.30cm2 C.24cm2 D.72cm2
8.我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米 B.7.5平方千米 C.15平方千米 D.30平方千米
9.如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
A.南偏东30° B.北偏东30° C.南偏东 60° D.南偏西 60°
10.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
二、填空题
11.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______.
12.如图,已知图中小正方形在格点上,则△ABC的面积为__________.
13.如图,在四边形ABCD中,,,,,AB⊥BC,四边形ABCD的面积为___________________.
14.若一个三角形的三边长之比为5∶12∶13,且周长为60 cm,则它的面积为________ cm2.
三、解答题
15.已知:如图,在四边形ABCD中,AB=BC,AD2+CD2=2AB2,CD⊥AD.
(1)求证:AB⊥BC.
(2)若AB=3CD,AD=17,求四边形ABCD的周长.
16.如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,求∠BCD的度数
17.在方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
(1)图1中线段的长是___________;请判断的形状,并说明理由.
(2)请在图2中画出,使,,三边的长分别为,,.
(3)如图3,以图1中的,为边作正方形和正方形,连接,求的面积.
18.在一次“构造勾股数”的探究性学习中,老师给出了下表:
m 2 3 3 4 …
n 1 1 2 3 …
a 22+12 32+12 32+22 42+32 …
b 4 6 12 24 …
c 22﹣12 32﹣12 32﹣22 42﹣32 …
其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a= ,b= ,c= .
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例
答案
1.D
2.C
3.D
4.D
5.C
6.C
7.C
8.B
9.C
10.B
11.17,144,145
12.5
13.
14.120
15.(1)证明:连接AC.
∵CD⊥AD,
∴AD2+CD2=AC2,
∵AD2+CD2=2AB2,AB=BC,
∴AC2=AB2+BC2,
∴∠ABC=90°,
∴AB⊥BC.
(2)设CD=k,则AB=BC=3k,
∵∠ABC=90°,
∴AC2=18k2,
在Rt△ACD中,∵AC2=CD2+AD2,
∴18k2=172+k2,
∴k=,
∴CD=,AB=BC=3,
∴四边形ABCD的周长=AB+BC+AD+CD=17+7.
16.解:∵∠B=90°,AB=BC=3,
∴AC===3 ,,∠BAC=∠BCA=45°,
又∵CD=,DA=5,
∴AC2+CD2=18+7=25,AD2=25,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴∠ACD=90°,
∴∠BCD=∠BCA+∠DCA=45°+90°=135°.
17.解:(1)AB=,△ABC为直角三角形,
理由是:AB==,AC==,BC=5,
∵,
∴△ABC为直角三角形;
(2)如图,即为所画三角形:
(3)∵∠BAC=90°,∠BAR=∠CAD=90°,
∴∠RAD=90°,
∵ AR=AB=,AD=AC=,
∴=5.
18.解:(1)当m=2,n=1时,a=5、b=4、c=3,
∵32+42=52,
∴a、b、c的值能为直角三角形三边的长;
(2)观察得,a=m2+n2,b=2mn,c=m2﹣n2;
(3)以a,b,c为边长的三角形一定为直角三角形,
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形
