人教版八年级下数学18.1.1平行四边形的边、角性质课件(第一课时 14张)
文档属性
| 名称 | 人教版八年级下数学18.1.1平行四边形的边、角性质课件(第一课时 14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-27 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角性质
做一做
在小学,我们已经认识了平行四边形,在图中找出平行四边形,并把它们勾画出来.
学习目标:
1、理解并掌握平行四边形的定义;
2、能根据定义探究平行四边形的性质;
3、了解平行四边形在生活中的应用实例,能根据平行四边形的性质解决简单的实际问题。
自学指导:
阅读教材P40—P42,时间:6分钟,完成下列任务:
1、由P40中的“做一做”,了解并掌握平行四边形的定义;
2、由P40-P41中的“探究:,推导得出平行四边形的性质,如何用数学语言叙述?
3、阅读例题1、例题2,掌握平行四边形性质的实际应用。
1.定义:
两组对边分别平行的四边形叫做平行四边形.
3.记作:
□ABCD
2.几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
两组对边分别平行
自学检测
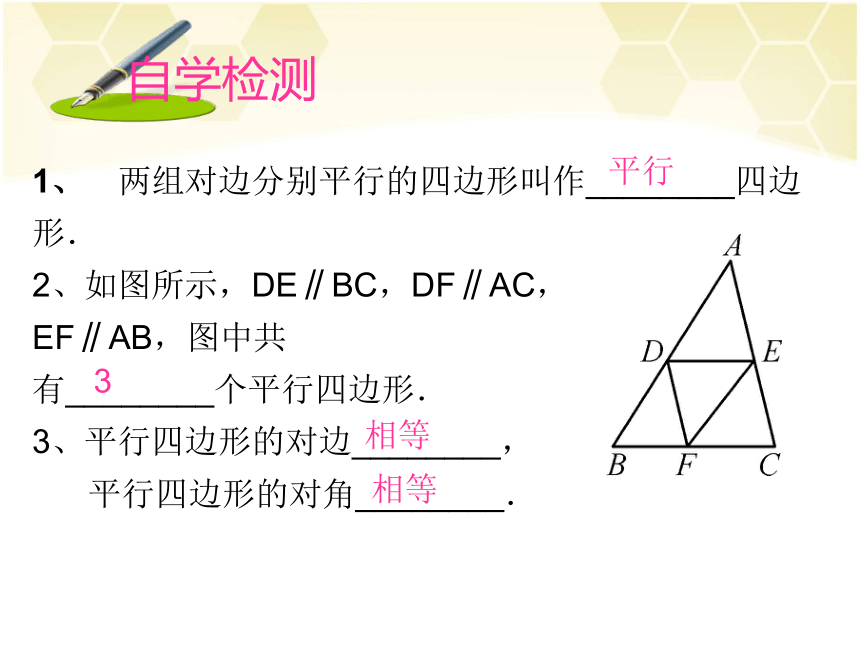
1、 两组对边分别平行的四边形叫作________四边形.
2、如图所示,DE∥BC,DF∥AC,
EF∥AB,图中共
有________个平行四边形.
3、平行四边形的对边________,
平行四边形的对角________.
平行
3
相等
相等
自学检测
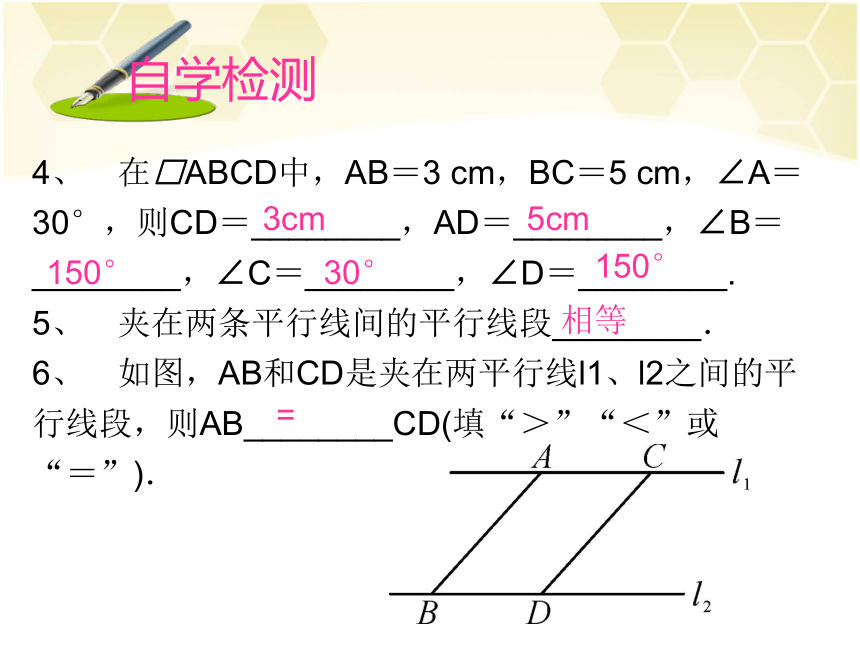
4、 在□ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=________,AD=________,∠B=________,∠C=________,∠D=________.
5、 夹在两条平行线间的平行线段________.
6、 如图,AB和CD是夹在两平行线l1、l2之间的平行线段,则AB________CD(填“>”“<”或“=”).
3cm
5cm
150°
30°
150°
相等
=
一展身手
1、若平行四边形中两个内角的度数比为1:2,则其中较大的内角是 度.
120
2、如图,已知E、F是平行四边形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
求证:△ABE≌△CDF.
一展身手
证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS)
练习
2.如图,在□ABCD中,∠ABC=68°,BE平分∠ABC,
交AD于点E.AB=2cm,ED=1cm.
(1)求∠A,∠C,∠D的度数;
(2)求□ABCD的周长.
解(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D=68°.
∴∠A=∠C=180°-68°=112°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC=∠BAE.
∴AB=AE=2cm.
∴AD=2+1=3(cm).
∴□ABCD的周长为:3+2+3+2=10(cm).
挑战自我
如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF.
证明:∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∴∠BCA=∠DAC,
又∵AE=CF,
∴EC=AF,
在△BCE和△DAF中,
∴△BCE≌△DAF(SAS),
∴BE=DF.
1. 概念:
四边形
两组对边分别平行
平行四边形
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
当堂训练:
见学案
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角性质
做一做
在小学,我们已经认识了平行四边形,在图中找出平行四边形,并把它们勾画出来.
学习目标:
1、理解并掌握平行四边形的定义;
2、能根据定义探究平行四边形的性质;
3、了解平行四边形在生活中的应用实例,能根据平行四边形的性质解决简单的实际问题。
自学指导:
阅读教材P40—P42,时间:6分钟,完成下列任务:
1、由P40中的“做一做”,了解并掌握平行四边形的定义;
2、由P40-P41中的“探究:,推导得出平行四边形的性质,如何用数学语言叙述?
3、阅读例题1、例题2,掌握平行四边形性质的实际应用。
1.定义:
两组对边分别平行的四边形叫做平行四边形.
3.记作:
□ABCD
2.几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
两组对边分别平行
自学检测
1、 两组对边分别平行的四边形叫作________四边形.
2、如图所示,DE∥BC,DF∥AC,
EF∥AB,图中共
有________个平行四边形.
3、平行四边形的对边________,
平行四边形的对角________.
平行
3
相等
相等
自学检测
4、 在□ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=________,AD=________,∠B=________,∠C=________,∠D=________.
5、 夹在两条平行线间的平行线段________.
6、 如图,AB和CD是夹在两平行线l1、l2之间的平行线段,则AB________CD(填“>”“<”或“=”).
3cm
5cm
150°
30°
150°
相等
=
一展身手
1、若平行四边形中两个内角的度数比为1:2,则其中较大的内角是 度.
120
2、如图,已知E、F是平行四边形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
求证:△ABE≌△CDF.
一展身手
证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS)
练习
2.如图,在□ABCD中,∠ABC=68°,BE平分∠ABC,
交AD于点E.AB=2cm,ED=1cm.
(1)求∠A,∠C,∠D的度数;
(2)求□ABCD的周长.
解(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D=68°.
∴∠A=∠C=180°-68°=112°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC=∠BAE.
∴AB=AE=2cm.
∴AD=2+1=3(cm).
∴□ABCD的周长为:3+2+3+2=10(cm).
挑战自我
如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF.
证明:∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∴∠BCA=∠DAC,
又∵AE=CF,
∴EC=AF,
在△BCE和△DAF中,
∴△BCE≌△DAF(SAS),
∴BE=DF.
1. 概念:
四边形
两组对边分别平行
平行四边形
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
当堂训练:
见学案
